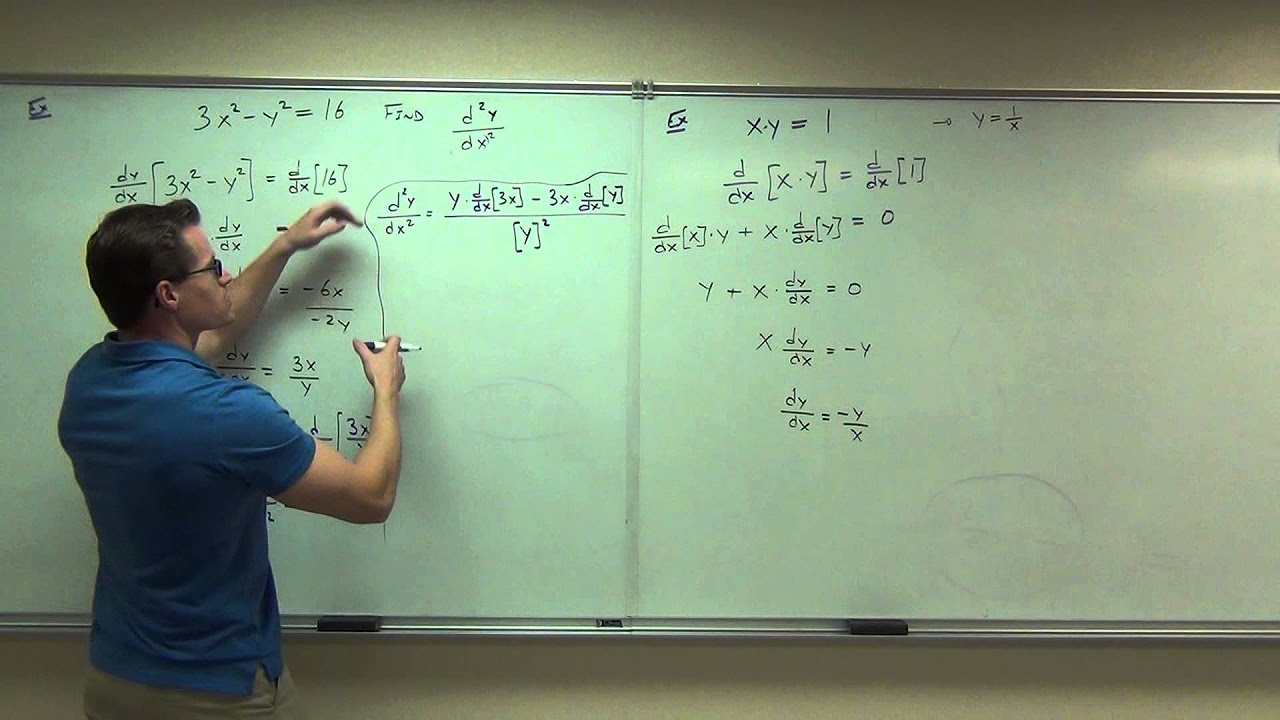Unit II: Lec 5 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT OpenCourseWare lecture on Implicit Differentiation explores the concept of deriving functions that are not explicitly solvable for 'y' in terms of 'x'. The professor illustrates how to differentiate equations implicitly, assuming 'y' is a function of 'x', and discusses the geometric implications, including the identification of vertical and horizontal tangents. Examples include differentiating complex algebraic equations and applying the method to physical problems like related rates, showcasing the power of calculus in analyzing constrained systems.
Takeaways
- 📘 Implicit Differentiation is a technique used when variables are not explicitly solvable in terms of each other, allowing for the derivation of one variable with respect to another without isolating the variable first.
- 🔑 The assumption that 'y' can be expressed as a function of 'x', which makes the given equation an identity, is fundamental to implicit differentiation. This means that replacing 'y' with its function of 'x' should satisfy the equation for all values of 'x' and 'y'.
- 🧩 The difference between an equation (conditional equality) and an identity (absolute equality) is crucial. An identity holds true for all values of the variable, while an equation may only hold under specific conditions.
- ⚖️ When differentiating an identity, the same rules apply as with explicit expressions. For example, the product rule is used when differentiating a product of two functions.
- 🔍 The example of 'x' times 'y' equals 1 illustrates how implicit differentiation works. By differentiating both sides with respect to 'x', one can find the derivative 'dy/dx' in terms of 'x' and 'y'.
- 📐 The lecture uses the equation 'x^2 + y^2 = 25' to demonstrate implicit differentiation, showing how to find 'dy/dx' for a circle and highlighting the multivalued nature of 'y' as a function of 'x'.
- 🤔 The potential issue of vertical tangents is discussed, indicating points where the function is not single-valued and differentiation with respect to 'x' may not be straightforward.
- 🔄 The concept of related rates is introduced, where the rates of change of different variables are related through an identity, such as in the motion of a particle along a constrained path.
- 📉 The example of the curve 'x^8 + x^6y^4 + y^6 = 3' is used to show a case where explicit solution for 'y' in terms of 'x' is difficult, but implicit differentiation can still find 'dy/dx'.
- ⏹ The importance of understanding the geometric interpretation and the physical meaning behind the mathematical process of implicit differentiation is emphasized for a deeper understanding of the subject.
- 🔚 The summary of the lecture highlights the importance of recognizing implicit relationships in mathematical expressions and the ability to differentiate these relationships under the right conditions.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is Implicit Differentiation, which is a method used to find the derivative of a function when it is not explicitly given in terms of the independent variable.
Why is the concept of single-valued functions and one-to-one functions relevant to implicit differentiation?
-The concept of single-valued functions and one-to-one functions is relevant because implicit differentiation assumes that 'y' can be expressed as a function of 'x', which is a key consideration when differentiating equations that are not easily solvable for 'y' in terms of 'x'.
What is the difference between an equation and an identity in mathematics?
-An equation is a statement that asserts the equality of two expressions, which may or may not be true for certain values of the variables involved. An identity, on the other hand, is a statement that is true for all values of the variables, meaning it holds universally regardless of the variable values.
How does implicit differentiation handle cases where the equation is not easily solvable for 'y' in terms of 'x'?
-Implicit differentiation handles such cases by assuming that 'y' is a function of 'x' that makes the given equation an identity. It then differentiates both sides of the equation with respect to 'x', using the appropriate rules of differentiation, to find the derivative 'dy/dx'.
What is the geometric intuition behind assuming 'y' as a function of 'x' in implicit differentiation?
-The geometric intuition is that for every value of 'x', there is a corresponding value of 'y' that satisfies the equation, forming a curve. Implicit differentiation assumes that this curve can be traced by a function 'y(x)', even when it is not possible to explicitly solve for 'y'.
Can implicit differentiation be used when the equation has multiple solutions for 'y' in terms of 'x'?
-Yes, implicit differentiation can be used even when there are multiple solutions for 'y' in terms of 'x'. However, it is important to consider the context and constraints of the problem to determine which solution is relevant.
What is the significance of differentiating both sides of an equation with respect to 'x'?
-Differentiating both sides of an equation with respect to 'x' allows us to find the rate of change of one variable with respect to another. This is particularly useful in implicit differentiation, as it enables us to find the derivative of 'y' with respect to 'x' without explicitly solving for 'y'.
How does the lecture illustrate the application of implicit differentiation using the equation 'x^2 + y^2 = 25'?
-The lecture illustrates the application by differentiating the equation 'x^2 + y^2 = 25' with respect to 'x', assuming 'y' is a function of 'x'. This results in an expression for 'dy/dx' in terms of 'x' and 'y', which can be used to find the slope of the tangent to the curve at any point.
What is the physical interpretation of differentiating an equation with respect to time 't'?
-Differentiating an equation with respect to time 't' allows us to find the rates of change of variables with respect to time. This is useful in physics for analyzing motion, where 'x' and 'y' might represent positions, and 'dx/dt' and 'dy/dt' represent velocities in the x and y directions, respectively.
What is the importance of understanding the conditions under which implicit differentiation is valid?
-Understanding the conditions under which implicit differentiation is valid ensures that the mathematical assumptions made are justified, and the results obtained are accurate. It helps to avoid errors in situations where the function 'y' may not be single-valued or where the curve has vertical tangents.
Outlines
📚 Introduction to Implicit Differentiation
The narrator introduces the video's focus on implicit differentiation, emphasizing its importance in MIT OpenCourseWare's educational offerings. The professor begins by discussing the relationship between implicit differentiation and single-valued functions, using the expression 'y = f(x)' to illustrate the assumption that 'y' can be explicitly solved in terms of 'x'. The lecture then delves into the complexity of solving equations where 'x' and 'y' are implicitly related, such as 'x^8 + x^6y^4 + y^6 = 3', and introduces the concept of identities in differentiation.
🔍 The Difference Between Equations and Identities
This paragraph explores the distinction between conditional equalities (equations) and absolute equalities (identities). The professor uses 'x^2 = 4' as an example to show that while 'x' can be either 2 or -2, 'x^2' is not synonymous with 4. Identities, such as 'x^2 - 1 = (x + 1)(x - 1)', hold true for all values of 'x'. The importance of recognizing this difference is highlighted when differentiating expressions, as it affects the validity of the derivative operations.
📘 Implicit Differentiation Methodology
The professor explains the process of implicit differentiation, using the identity 'xy = 1' as an example. By differentiating both sides with respect to 'x' and applying the product rule, the derivative 'dy/dx' is found to be '-y/x'. The method is then illustrated with the equation 'x^2 + y^2 = 25', leading to the discovery that 'dy/dx' can be found using similar differentiation techniques, resulting in 'dy/dx = -x/y'.
🤔 Multivalued Functions and Implicit Differentiation
The lecture addresses the complexities that arise when 'y' is a multivalued function of 'x', as in the case of 'x^2 + y^2 = 25'. The professor demonstrates that while 'y' can be explicitly solved for in terms of 'x', the resulting function is multivalued, leading to potential issues when differentiating implicitly. The importance of considering the geometric implications and the existence of functions that satisfy the identity is discussed.
📉 Analyzing Tangent Lines and Vertical Asymptotes
The professor examines the implications of implicit differentiation on the geometry of a curve, specifically focusing on the equation 'x^8 + x^6y^4 + y^6 = 3'. The analysis reveals conditions under which the slope of the tangent to the curve is zero (indicating a horizontal tangent) or undefined (indicating a vertical tangent). The symmetry of the curve with respect to both axes is also noted.
🔄 Generalizing Related Rates and Parametric Differentiation
The final paragraph extends the concept of implicit differentiation to related rates and parametric differentiation. The professor illustrates this with an example involving a particle moving along the curve 'x^2 + y^2 = 25', where 'x' and 'y' are functions of time 't'. By differentiating the equation with respect to 't', the relationship between 'dx/dt' and 'dy/dt' is established, showcasing the power of calculus in analyzing physical phenomena.
👋 Conclusion and Acknowledgment
In conclusion, the professor emphasizes the importance of understanding implicit relationships in calculus and the ability to differentiate under the assumption that an appropriate identity exists. The lecture wraps up with a reminder of the importance of these concepts in advanced calculus and an acknowledgment of the Gabriella and Paul Rosenbaum Foundation for funding the video's publication.
Mindmap
Keywords
💡Implicit Differentiation
💡Single-valued functions
💡Identities
💡Equation
💡Product Rule
💡Chain Rule
💡Differentiable Functions
💡Related Rates
💡Tangent Line
💡Polynomial Equation
💡Fractional Exponent
Highlights
Introduction to Implicit Differentiation and its relation to single-valued functions.
Assumption that 'y' can be solved explicitly in terms of 'x' is often implicit but not always straightforward.
Exploration of the complexity in solving equations like 'x^8 + x^6y^4 + y^6 = 3' for 'y' explicitly in terms of 'x'.
Understanding the geometric intuitiveness of implicit differentiation despite its rigorous mathematical justification being complex.
The concept of identity in equations and the importance of differentiating between an equation and an identity.
Illustration of how to differentiate an identity using the example 'x * y = 1'.
Explanation of the product rule in the context of implicit differentiation.
Verification of the implicit differentiation method using an example that can also be solved explicitly.
Introduction of the relationship between 'x' and 'y' in implicit differentiation and the importance of related rates.
Differentiation of the equation 'x^2 + y^2 = 25' using implicit differentiation and the discovery of multivalued functions.
Analysis of the limitations of implicit differentiation near points where the function is not single-valued.
Generalization of implicit differentiation to include differentiation of fractional exponents.
Application of implicit differentiation to find the slope of a curve at a specific point.
Identification of points where the slope of the curve is zero or undefined, indicating horizontal or vertical tangents.
Discussion on the symmetry of the curve with respect to both axes and its implications.
The importance of being cautious with implicit differentiation at points where the curve may not be single-valued.
Extension of implicit differentiation to related rates and physical applications, such as the motion of a particle along a curve.
Conceptual summary of implicit differentiation and its significance in understanding the relationship between variables.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: