Calculus Chapter 5 Lecture 57 Calculus Redux
TLDRIn this calculus lecture, Professor Greist reflects on the journey through the course, highlighting the achievements and limitations of calculus. The lecture explores the boundary between what is possible and impossible in calculus, using examples such as the integral of the Gaussian function, Euler's theorem, and the sum of reciprocals of squares equaling π²/6. It emphasizes the complexity of certain mathematical truths and the effort required to understand them, while also congratulating students on their perseverance through the challenging course.
Takeaways
- 🎓 The lecture concludes the Calculus course, acknowledging the difficulty and perseverance of the students.
- 📚 The course covered a wide range of topics including limits, derivatives, integrals, ordinary differential equations, and Taylor series.
- 🚫 The professor highlights the limitations of calculus, such as the inability to easily compute certain integrals and prove certain theorems without additional techniques.
- 🧮 An example of a complex integral involving the Gaussian function is discussed, which is fundamental in probability and statistics.
- 📉 The attempt to solve the Gaussian integral using term-by-term integration failed due to the nature of the improper integral.
- 📈 An alternative strategy involving the limit of cosine raised to the power of n is introduced as a potential method to tackle difficult integrals.
- 🔍 The proof of the limit involving the cosine function is outlined, utilizing the Taylor expansion and properties of limits.
- 🔧 The difficulty of integrating the limit of the cosine function over the real line is mentioned, hinting at the need for more advanced techniques.
- 🔄 The concept of Euler's theorem, e^(iT) = cos(T) + i*sin(T), is revisited, and the challenge of proving it without circular reasoning is discussed.
- 🌀 The idea of using ordinary differential equations to prove Euler's theorem is introduced, leading to a system of coupled differential equations.
- 📝 The sum of the series 1/n^2 converging to π^2/6 is examined, and the complex proof involving the function arcsin(x) and its Taylor series is briefly described.
- 🏆 The lecture concludes by emphasizing the deep and sometimes elusive nature of mathematical truths, and the value of striving for understanding even the most difficult concepts.
Q & A
What is the main theme of Professor Greist's lecture 57 in calculus?
-The main theme of the lecture is to reflect on the capabilities and limitations of calculus, discussing what can and cannot be done with the tools learned in the course.
Why is the integral from minus infinity to infinity of e to the minus x squared over 2 dx significant?
-This integral is significant because it is the result that establishes a standard Gaussian as a probability density function, which is crucial in probability and statistics.
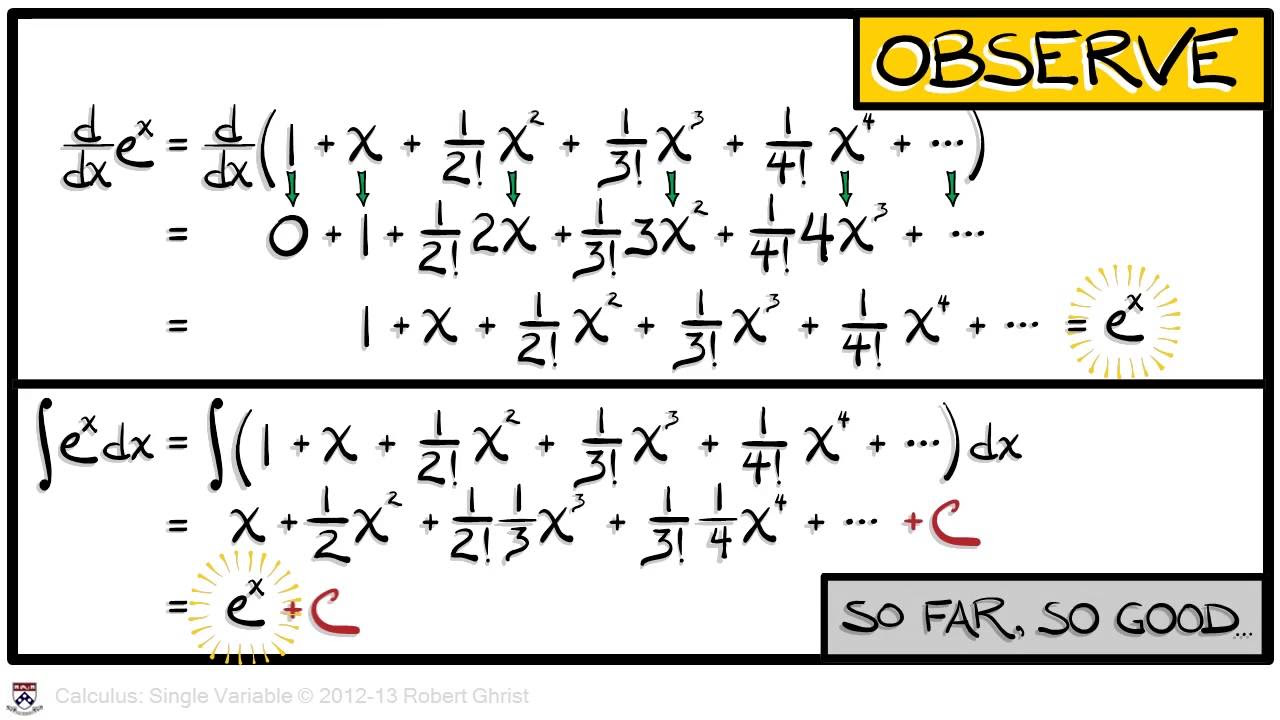
What is the standard expansion for e to the x used in the lecture?
-The standard expansion for e to the x is a sum over N where each term is 1 over N factorial times (negative x) to the power of N.
Why is integrating term by term not effective for the improper integral mentioned in the lecture?
-Integrating term by term is not effective for the improper integral because it does not converge to a meaningful result, making it nonsensical to evaluate from negative infinity to positive infinity.
What alternative strategy is suggested to evaluate e to the minus x squared over 2?
-The alternative strategy is to show that e to the minus x squared over 2 equals the limit as n goes to infinity of cosine raised to the nth power of X over the square root of n.
How is Euler's theorem e to the I T equals cosine t plus I times sine of T related to ordinary differential equations?
-Euler's theorem can be related to ordinary differential equations by considering e to the I T as a function of T and using the differential equation Z prime equals I times Z, which leads to a system of coupled differential equations for the real and imaginary parts of Z.
What is the issue with using Taylor series to prove Euler's theorem directly?
-The issue is that the Taylor series expansions for cosine and sine were derived using Euler's theorem, so using them to prove the theorem would be circular logic.
What is the series sum that equals PI squared over 6 and why is it challenging to prove?
-The series sum is the sum over N of 1 over N squared. Proving it equals PI squared over 6 is challenging because it requires advanced integration techniques and a deep understanding of series and their convergence.
How does the lecture relate the series sum of 1 over N squared to the integral involving the arc sine function?
-The lecture uses the Taylor series for the arc sine function and integrates it term by term, eventually relating the result to the sum of 1 over N squared and showing it equals PI squared over 6.
What is the final message Professor Greist conveys to the students at the end of the lecture?
-The final message is to acknowledge the difficulty and depth of mathematical truths, to appreciate the effort required to understand them, and to congratulate the students for making it through the challenging course.
Outlines
📚 Reflecting on Calculus: Achievements and Limitations
Professor Greist concludes the calculus course by reflecting on the journey, acknowledging the challenges faced by students and their perseverance. The lecture focuses on the capabilities of calculus, such as understanding limits, derivatives, integrals, ordinary differential equations, and Taylor series, while also addressing its limitations. An example of an integral that cannot be solved using the course's tools is presented, highlighting the boundary between the possible and the impossible in calculus. The integral of e^(-x^2/2) from minus infinity to infinity is discussed, showing its importance in probability and statistics, but also demonstrating the limitations when attempting to solve it using term-by-term integration due to the absolute convergence.
🔍 Exploring the Limits of Calculus: Euler's Theorem and Beyond
The script delves into Euler's theorem, e^(iT) = cos(T) + i*sin(T), which was assumed without proof earlier in the course. It explores potential methods for proving this theorem, such as using Taylor series expansions or considering it as a system of coupled ordinary differential equations. The limitations of the current course in solving such systems are acknowledged, and it is suggested that multivariable calculus will provide the necessary tools to tackle this problem more effectively. The discussion also touches on the difficulty of proving certain mathematical truths and the effort required to ascertain them.
📉 The Zeta Function and the Quest for PI²/6
The final paragraph discusses the series sum of 1/n² and its relation to PI²/6. An attempt is made to prove this result using the function u = arcsin(x) and integrating it from 0 to PI/2. The presence of PI² in the result is highlighted as a critical piece. The Taylor series for arcsin(x) is substituted into the integral, and after a complex process of integration and simplification, the sum of 1/(2n-1)² is obtained, which is related to the original series. The connection to PI²/6 is established through further argument involving a geometric series, showcasing the deep and sometimes elusive nature of mathematical truths.
Mindmap
Keywords
💡Calculus
💡Integral
💡Taylor Series
💡Euler's Theorem
💡Ordinary Differential Equations (ODEs)
💡Improper Integral
💡Limit
💡Multivariable Calculus
💡Zeros of X to the Fourth
💡Pi Squared Over 6
💡Arcsine Function
Highlights
Professor Greist concludes the calculus course with a reflective look at its capabilities and limitations.
Students are encouraged to appreciate the hard work and perseverance through the course.
The course covers a wide range of topics including limits, derivatives, integrals, ordinary differential equations, and Taylor series.
The boundary between what is possible and what is beyond reach in calculus is explored.
An example of a difficult integral with implications in probability and statistics is introduced.
The integral of e^(-x^2/2) from minus infinity to infinity equals the square root of 2 pi.
An attempt to solve the integral using term-by-term integration fails due to the improper nature of the integral.
A novel strategy is presented to show e^(-x^2/2) equals the limit of cos(x/√n)^n as n approaches infinity.
The proof of the novel strategy involves taking logarithms and using Taylor expansions.
The difficulty of evaluating the integral with the novel strategy is discussed, hinting at the need for more advanced techniques.
Euler's theorem e^(iT) = cos(T) + i*sin(T) is revisited, and the challenge of proving it without circular logic is highlighted.
A system of coupled ordinary differential equations is derived from Euler's theorem.
The inability to solve the system of coupled equations within the course's scope is acknowledged.
The sum of 1/n^2 from 1 to infinity equals π^2/6 is discussed as a series that is known to converge but challenging to prove.
A proof involving the function u = arcsin(x) and its integration is outlined.
The use of Taylor series for arcsin(x) and the subsequent integration is described as a complex but feasible approach.
The final result of the series proof, π^2/6, is derived through a series of mathematical manipulations.
The difficulty of some mathematical truths is emphasized, and the importance of striving for understanding is highlighted.
The lecture concludes with congratulations to the students for completing the course and advice to prepare for the final exam.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: