The Subtle Reason Taylor Series Work | Smooth vs. Analytic Functions
TLDRThis video explores the intricacies of calculating functions like e^x, sin(x), and cos(x) using Taylor Series, a method that approximates functions based on their derivatives at a specific point. It reveals the surprising fact that while Taylor Series can perfectly match certain functions like e^x globally, many others do not equal their Taylor expansions on any interval. The video explains why some functions, termed 'analytic,' match their Taylor Series everywhere, while others, like the smooth but non-analytic function e^(-1/x), do not. It also touches on the complex plane, where 'smooth' and 'analytic' coincide, and ends by highlighting the utility of non-analytic functions in creating 'bump' functions for localized perturbations.
Takeaways
- 📚 The script discusses how to calculate functions like e^x, sin(x), and cos(x) at any given x-value, often using Taylor Series expansions.
- 📈 It explains that functions can be approximated near an input value where the function and its derivatives are easy to calculate, using e^x as an example.
- 🔍 The script highlights the process of improving approximations from linear to higher-degree polynomials, eventually leading to the Taylor Series.
- 🌟 The Taylor Series for e^x at x = 0 converges for all possible values of x, allowing for precise calculations of e^x at any x.
- 😲 The script points out the surprising fact that Taylor Series, constructed using local information, can perfectly equal the function globally.
- 🧐 It introduces the concept of Taylor's Theorem, which quantifies the error between the Taylor polynomial approximation and the original function over a given interval.
- 📉 The script explains that the error in the Taylor approximation depends on the value of the next higher derivative of the function between the approximation point and the point of interest.
- 📚 The importance of higher-order derivatives' growth rate is emphasized, as functions like e^x, sin(x), and cos(x) have derivatives that grow slower than factorial, leading to convergence of their Taylor Series.
- 🌐 The difference between real and complex analysis is touched upon, noting that in the complex plane, smooth functions are automatically analytic (holomorphic).
- 🤔 The script challenges the assumption that smooth functions are necessarily analytic, providing a counterexample and explaining the rarity of such functions.
- 🛠 It concludes by noting the utility of non-analytic smooth functions, such as in creating 'bump' functions for localized perturbations without breaking smoothness.
Q & A
What is the basic idea behind calculating functions like e^x, sin(x), or cos(x) at any given x-value?
-The basic idea is to approximate the function near an input value where the function and its derivatives are easy to calculate. This is typically done using Taylor Series or Taylor Expansion, which involves constructing polynomials that match the function's value and derivatives at a specific point.
Why is e^x easy to calculate at x = 0?
-e^x is easy to calculate at x = 0 because anything to the zero power is 1. Additionally, all the derivatives of e^x are just copies of itself, meaning they are also easy to evaluate at x = 0 and are all equal to 1.
What is a linear approximation and how does it relate to the tangent line of a curve?
-A linear approximation is a method of approximating a function near a certain point using a linear function. It relates to the tangent line of a curve because the tangent line at a point on the curve is the best linear approximation since it matches both the value (height) and the slope (derivative) of the curve at that point.
How does a quadratic approximation improve upon a linear approximation?
-A quadratic approximation is better than a linear one because it not only matches the function's value and first derivative at a given point but also matches the second derivative. This additional information allows for a more accurate representation of the function near the point of approximation.
What is the Taylor Series or Taylor Expansion?
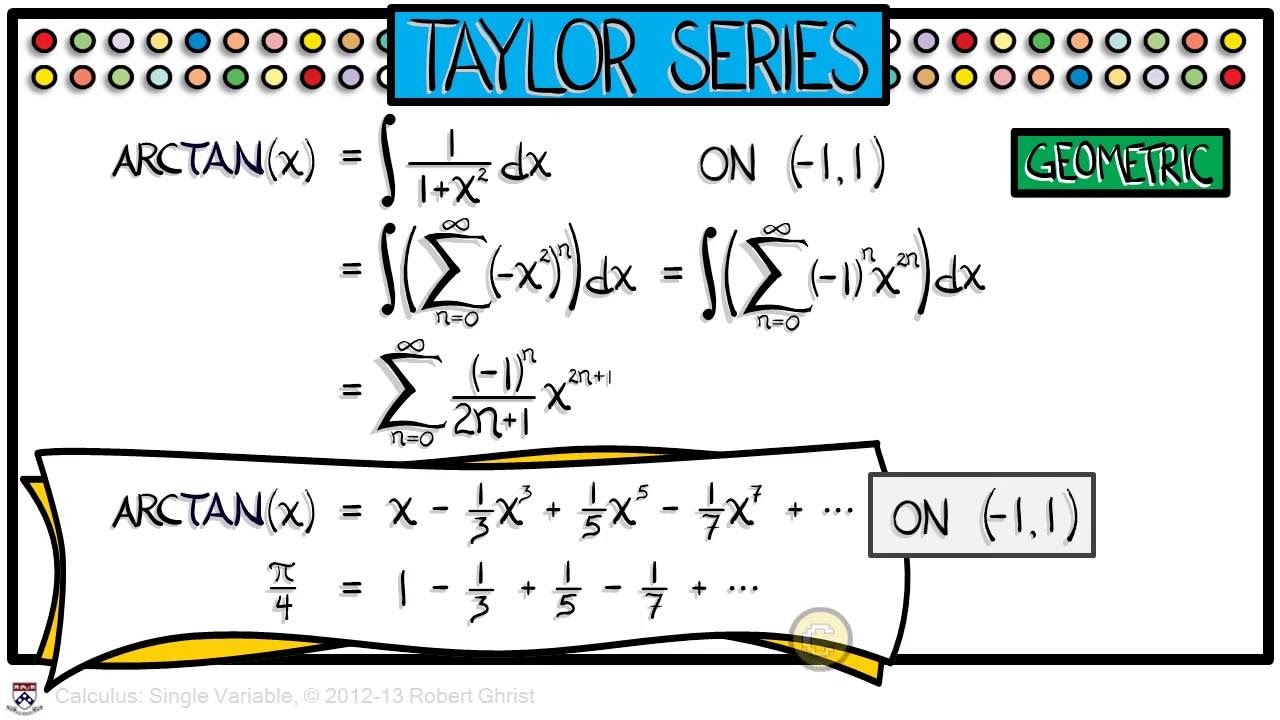
-The Taylor Series or Taylor Expansion is a representation of a function as an infinite sum of terms calculated from the values of its derivatives at a single point. It is used to approximate the function near that point and, in some cases, can equal the function for all x values where the series converges.
Why might the Taylor Series for e^x be considered surprising or 'ridiculous'?
-The Taylor Series for e^x might be considered surprising because it uses only local information about the function at x = 0 to approximate the function's behavior everywhere. Despite this, it perfectly equals the function for all x values where the series converges, which is an unexpected and powerful result.
What is the difference between an analytic function and a non-analytic function?
-An analytic function is one that equals its Taylor series on some interval around the point of expansion. In contrast, a non-analytic function does not necessarily equal its Taylor series even on a small interval around the expansion point, regardless of how smooth it may be.
What is Taylor's Theorem and how does it relate to the error of Taylor approximations?
-Taylor's Theorem provides a way to measure the error between a Taylor polynomial approximation and the original function over a given interval. It states that the error, or 'remainder', is given by the (n+1)-derivative of the function evaluated at some point between the expansion point and the input point, divided by (n+1)-factorial, times the power of the difference between the input point and the expansion point.
Why do functions like e^x, sin(x), and cos(x) equal their Taylor series at all x-values?
-Functions like e^x, sin(x), and cos(x) equal their Taylor series at all x-values because their higher-order derivatives grow much slower than n-factorial as the derivative order n increases. In fact, their higher-order derivatives stay bounded, which allows the remainder term in Taylor's Theorem to approach zero as n increases.
What is a 'bump' function and why is it useful?
-A 'bump' function is a type of function that is zero everywhere except for a small region, yet remains smooth even at the boundary where it transitions from zero to non-zero. It is useful for creating localized perturbations in a function without breaking smoothness, which can be important for numerical stability in algorithms.
How does the behavior of functions in the complex plane differ from those on the real line?
-In the complex plane, the concepts of 'smooth' and 'analytic' coincide. If a complex-valued function has derivatives of all orders in an open region of the complex plane, it is automatically analytic there. Moreover, having a first derivative on an open region automatically makes it smooth, which is a significant difference from real analysis where non-analytic smooth functions can exist.
Outlines
📚 Introduction to Function Approximation
The video begins with an introduction to the concept of approximating functions such as e^x, sin(x), and cos(x) at any given x-value, a topic that might be familiar to those who have studied calculus. The method involves approximating the function near an input value where it and its derivatives are easy to calculate, using e^x as an example. The function e^x is simple to evaluate at x = 0, and all its derivatives at this point are also easy to find, being equal to 1. The video suggests starting with a linear approximation and then progressively improving it with higher-degree polynomials, ultimately leading to the Taylor Series, which exactly equals the function for all x-values where it converges. The video also mentions a sponsor, Surfshark VPN, which offers online security and privacy features.
🔍 The Paradox of Taylor Series
This paragraph delves into the surprising nature of Taylor Series, which, despite being constructed using only local information about a function at a single point, can perfectly equal the function elsewhere. The video challenges the assumption that Taylor polynomials will improve to arbitrary precision and reach perfect equality in the limit, highlighting the fact that these polynomials only use the value and derivatives of the function at x = 0. It introduces the concept of 'remainder' from Taylor's Theorem, which measures the error between the Taylor polynomial approximation and the original function over a given interval, and explains how this error depends on the value of the next higher derivative of the function between the point of approximation and the point being evaluated.
🧩 Analytic Functions and the Complex Plane
The final paragraph discusses the special class of functions known as 'analytic functions', which are those that equal their Taylor expansions not just at the point of expansion, but also in an interval around it. It explains that while non-analytic smooth functions exist and can be pathological, most functions encountered in regular mathematical work are analytic. The video also touches on the concept of 'holomorphic' functions in the complex plane, which are automatically smooth and analytic if they have a first derivative in an open region. The complex plane is portrayed as a realm where functions behave more nicely due to fewer edge cases. The video concludes by acknowledging the importance of non-analytic smooth functions, such as their use in creating 'bump' functions, which are smooth except for a small region where they transition from zero to non-zero. The video ends with a hopeful note on the deeper understanding of Taylor series and function approximation.
Mindmap
Keywords
💡Surfshark VPN
💡Calculus
💡Approximation
💡Taylor Series
💡Derivatives
💡Linear Approximation
💡Quadratic Approximation
💡Taylor's Theorem
💡Analytic Functions
💡Holomorphic Functions
💡Bump Function
Highlights
Introduction of a common technique for calculating functions like e^x, sin(x), or cos(x) using approximations.
Explanation of approximating functions near an input value where the function and its derivatives are easy to calculate.
Use of e^x as an example function and its properties at x = 0 for approximation.
Concept of linear approximation and finding the tangent line formula at the point of tangency.
Improvement of approximation using higher-degree polynomials like quadratic and cubic.
Introduction of the Taylor Series as a method to calculate functions to any precision.
The convergence of the Taylor Series for e^x for all possible values of x.
Critique of the Taylor Series method, questioning its logical validity.
Discussion on the local information used in constructing polynomial approximations.
Example of a function whose Taylor expansion does not equal the function on any interval.
Introduction of Taylor's Theorem for measuring the error of Taylor polynomial approximations.
Explanation of how the error in Taylor approximation decreases as the order increases.
Definition and importance of 'analytic functions' and their properties.
Difference between analytic functions and non-analytic smooth functions.
Complex plane's unique properties where 'smooth' and 'analytic' coincide.
Introduction of 'holomorphic' functions and their automatic smoothness and analyticity.
The irony that complex numbers simplify the behavior of functions in the complex plane.
Use of non-analytic smooth functions in creating 'bump' functions with practical applications.
Conclusion emphasizing the depth and complexity of Taylor series and function approximation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: