Gravitational Potential and Gravitational Potential Energy

Cowen Physics
9 Oct 201909:11
EducationalLearning
32 Likes 10 Comments

TLDRThis video introduces the concept of gravitational potential, explaining its calculation and significance in physics. It clarifies the limitations of the gravitational potential energy equation and how to calculate absolute gravitational potential energy by defining zero potential energy at an infinitely distant point with no gravitational field strength. The video also differentiates between gravitational potential and potential energy, emphasizing the importance of understanding the work done per unit mass in a gravitational field. A practical example demonstrates the minimum work required to move an object from Earth's surface to a height of 2,000 kilometers, highlighting the importance of considering the changing gravitational field strength. The video concludes with a discussion on the graphical representation of gravitational potential and its relationship with gravitational field strength.

Takeaways
  • 🌐 Gravitational potential energy (GPE) is the energy required to lift an object against gravity, calculated as GPE = M*G*h, where M is mass, G is the gravitational constant, and h is the height.
  • 🚫 The GPE formula has limitations: it only applies in a uniform field and calculates the change in energy, not the absolute value.
  • 🌌 Absolute GPE is defined with respect to an infinitely distant point with no gravitational field strength, considered as zero potential energy.
  • πŸ”„ Gravitational potential (V) is the work done per unit mass to move an object from a point in a gravitational field to infinity, given by V = -G*M/R, where M is the mass of the celestial body and R is the distance from its center.
  • πŸ“‰ Gravitational potential is always negative because we increase it to reach zero, similar to electron energy levels in atoms.
  • πŸ”§ The symbol V for gravitational potential is used to differentiate it from voltage, which is work done per unit charge.
  • πŸ“ˆ Gravitational potential difference (Ξ”V) is the work needed to move an object from one location to another in a gravitational field, calculated by subtracting the potentials at the two locations.
  • πŸ”’ The work done to move an object is found by multiplying the mass of the object by the gravitational potential difference (W = m * Ξ”V).
  • 🌍 Example calculation: Moving a 100 kg object 2,000 km above Earth's surface requires ~1.49 x 10^9 Joules of work, considering the varying gravitational field strength.
  • πŸ“Š Gravitational potential graphs show an inverse relationship between potential and distance from the center of a celestial body, with the gradient representing the gravitational field strength.
  • πŸ”„ Integrating the gravitational field strength (G) over distance gives the change in gravitational potential (Ξ”V), and the area under the curve represents this change.
Q & A

  • What is the formula for calculating gravitational potential energy (GPE)?

    -The formula for calculating gravitational potential energy is GPE = m * g * h, where m is the mass of the object, g is the gravitational field strength, and h is the change in height.

  • What are the two limitations of the GPE formula?

    -The two limitations of the GPE formula are that it only works in a uniform field where the gravitational field strength (G) is known, and it can only calculate the change in gravitational potential energy from one location to another.

  • How is the absolute gravitational potential energy of a body defined?

    -The absolute gravitational potential energy of a body is defined by considering the infinitely distant point with no gravitational field strength as the location of zero potential energy. This means all absolute values of gravitational potential energy (GPA) are negative since we increase GPA to reach zero.

  • What is the relationship between gravitational potential and gravitational potential energy?

    -Gravitational potential is the work done per unit mass to move a mass from a position in a gravitational field to infinity. It is related to gravitational potential energy (GPE) by the equation GPE = m * gravitational potential, where m is the mass of the object.

  • What is the formula for calculating gravitational potential?

    -The formula for calculating gravitational potential (V) is V = -G * M / R, where G is the universal gravitational constant, M is the mass of the planet or object creating the field, and R is the distance from the center of the mass.

  • Why do we use a negative sign in the gravitational potential equation?

    -The negative sign in the gravitational potential equation indicates that we have defined gravitational potential energy as zero at its maximum value. This means that all absolute values of gravitational potential are negative because we increase potential energy to reach zero potential energy.

  • How does the gravitational field strength change as we move away from a planet?

    -As we move away from a planet, the gravitational field strength decreases according to an inverse square law. This means that the field strength is inversely proportional to the square of the distance from the center of the planet.

  • What is the gravitational potential difference and how is it calculated?

    -Gravitational potential difference (Ξ”V) is the difference in potential between two points in a gravitational field. It is calculated by finding the potential at each location and then subtracting one from the other, giving us the amount of work needed to move an object from one point to another.

  • How much work is required to move a 100 kg object 2,000 kilometers above the Earth's surface?

    -The work required to move a 100 kg object 2,000 kilometers above the Earth's surface is approximately 1.49 x 10^9 joules. This is calculated by finding the gravitational potential difference and then multiplying by the mass of the object.

  • What would be the incorrect result if we applied the GPE formula (m * g * h) to calculate the gravitational potential difference?

    -If we incorrectly applied the GPE formula to calculate the gravitational potential difference, we would get a value of 1.962 x 10^9 joules, which is higher than the correct value because it assumes that the gravitational field strength is constant all the way up to the 2,000 kilometer mark, which is not true.

  • How can we relate the graph of gravitational potential to the gravitational field strength?

    -The graph of gravitational potential against separation distance shows an inverse relationship. The gradient of this graph is equal to Ξ”V / Ξ”R, which is equal to -G / R^2, representing the gravitational field strength. By integrating the graph of gravitational field strength (G), we can obtain the gravitational potential difference (Ξ”V).

Outlines
00:00
🌌 Introduction to Gravitational Potential

This paragraph introduces the concept of gravitational potential and its relation to gravitational potential energy (GPE). It explains the formula for calculating a change in GPE, which is equal to the product of mass (M), the gravitational field strength (G), and the change in height. The limitations of this equation are also discussed, noting that it applies only to uniform fields and cannot calculate absolute GPE. The video then poses a question about how to calculate the absolute GPE of a body in a non-uniform field, setting the stage for a deeper exploration of the topic.

05:01
πŸ“ˆ Calculating Gravitational Potential and Potential Difference

This paragraph delves into the calculation of gravitational potential and potential difference. It explains that gravitational potential is the work done per unit mass to move a mass from a position in a gravitational field to infinity, which is essentially the GPE divided by the mass of the object. The formula for gravitational potential, V = -GM/R, is derived, and the units (joules per kilogram) are clarified. The paragraph then provides a step-by-step example calculation of the minimum work needed to move a 100 kg object from the Earth's surface to a height of 2,000 km above the surface. It corrects a common misconception about using the e=MGH equation for gravitational potential difference and emphasizes the importance of considering the changing gravitational field strength with distance. The paragraph concludes with a discussion on the graphical representation of gravitational potential against separation distance and how the gradient of this graph relates to the gravitational field strength.

Mindmap
Keywords
πŸ’‘Gravitational Potential
Gravitational Potential refers to the work done per unit mass to move an object from a position within a gravitational field to an infinite distance, where the gravitational field strength is zero. It is a scalar quantity with negative values, indicating the amount of work required to move an object against the gravitational force. In the video, this concept is used to calculate the work needed to move an object from the Earth's surface to a height of 2,000 kilometers above it.
πŸ’‘Gravitational Potential Energy (GPE)
Gravitational Potential Energy (GPE) is the energy an object possesses due to its position in a gravitational field. It is defined as the work done against gravity to move the object from a reference point to its current position. In the context of the video, GPE is calculated using the formula M*G*h, where M is the mass of the object, G is the gravitational constant, and h is the change in height. The video emphasizes the limitations of this formula, particularly its applicability only in uniform gravitational fields.
πŸ’‘Gravitational Field Strength
Gravitational Field Strength is a measure of the intensity of a gravitational field at a particular point in space. It is determined by the mass of the object creating the field and the distance from the object. The video explains that as an object moves further away from the Earth, the gravitational field strength decreases, which affects the calculation of gravitational potential energy and potential.
πŸ’‘Work Done
In the context of the video, work done refers to the effort required to move an object against the force of gravity. It is calculated as the force applied (in this case, the gravitational force) multiplied by the distance over which the force is applied. The work done is directly related to the change in gravitational potential energy, as it represents the energy transferred to or from the object when it is moved within a gravitational field.
πŸ’‘Universal Gravitational Constant (G)
The Universal Gravitational Constant (G) is a fundamental constant of nature that describes the strength of the gravitational force between two masses. In the video, G is used in the formulas for calculating gravitational potential energy and gravitational potential. It is a crucial component in understanding how the force of gravity affects the energy of objects in a gravitational field.
πŸ’‘Separation Distance (R)
Separation Distance (R) represents the distance between two masses in a gravitational context, such as the distance between the Earth and an object. In the video, R is used in the calculation of gravitational potential and gravitational potential energy. As R increases, the gravitational potential energy also increases, and the gravitational field strength decreases.
πŸ’‘Potential Difference (Ξ”V)
Potential Difference, denoted as Ξ”V, is the difference in gravitational potential between two points in a gravitational field. It quantifies the amount of work that would be needed to move an object from one point to another against the gravitational force. In the video, Ξ”V is calculated by subtracting the potential at one point from the potential at another, and this value is used to determine the minimum work required to move an object from the Earth's surface to a higher altitude.
πŸ’‘Electron Energy Levels
Electron Energy Levels are the quantized energy states that electrons can occupy within an atom. The video draws an analogy between these energy levels and gravitational potential energy, where each shell of electrons is considered to have negative energy, and energy must be added for an electron to escape the atom. This comparison helps to illustrate the concept of negative values in gravitational potential energy.
πŸ’‘Gravitational Force
The Gravitational Force is the attractive force that exists between any two masses. In the video, this force is described by the equation F = G/R^2, where F is the gravitational force, G is the universal gravitational constant, and R is the separation distance between the centers of the two masses. The gravitational force is what necessitates the work done to move an object against gravity.
πŸ’‘Inverse Relationship
An Inverse Relationship is a type of mathematical relationship where one quantity increases as another decreases. In the context of the video, the relationship between gravitational potential and separation distance is inverse, meaning as the distance from the Earth's surface (R) increases, the gravitational potential decreases. This relationship is graphically represented in the video's discussion of the graph of gravitational potential versus separation distance.
πŸ’‘Graphs
Graphs are visual representations of data or mathematical relationships. The video discusses a graph of gravitational potential versus separation distance, which illustrates the inverse relationship between potential and distance. The gradient of this graph represents the gravitational field strength, and the area under the graph represents the change in gravitational potential between two points.
Highlights

Introduction to the concept of gravitational potential.

Gravitational potential energy (GPE) calculation with the formula GPE = m*G*h.

Limitations of the GPE equation: it only works in a uniform field and calculates change in GPE, not absolute value.

Absolute gravitational potential energy is calculated considering an infinitely distant point with no gravitational field strength as zero potential energy.

Gravitational potential energy (GPE) increases as an object is lifted further from Earth, despite the Earth's gravitational field strength weakening.

The formula for gravitational potential is the GPE divided by the mass of the object, represented as V = -G*M/R.

Gravitational potential is analogous to electrical potential but is work done per unit mass rather than per unit charge.

Gravitational potential difference (Ξ”V) is the work needed to move an object from one location in a gravitational field to another.

Calculating the minimum work needed to move a 100 kg object 2,000 km above Earth's surface, considering Earth's mass, radius, and the universal gravitational constant.

Correct application of gravitational potential equations versus incorrect use of gravitational potential energy equations, which assume a constant gravitational field strength.

Gravitational potential graphs showing potential against separation distance, with an inverse relationship and a gradient equal to the negative gravitational field strength.

The area under a gravitational potential graph represents the change in gravitational potential between two points in the field.

Differentiating the gravitational potential equation yields the gravitational field strength equation.

Integration of the gravitational field strength equation gives the gravitational potential difference equation.

Scalar nature of gravitational potential, which, unlike gravitational field strength, always has negative values and can be added and subtracted like any other scalars.

Multiplying the gravitational potential difference by mass returns the work done, which can be used to calculate the energy requirements for moving objects in a gravitational field.

The concept of gravitational potential and potential difference is crucial for understanding the energy dynamics in gravitational fields.

Transcripts

Browse More Related Video

Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs

What is Gravitational Potential Energy - a deeper understanding

Gravitational and Elastic Potential Energy

Gravitational potential energy at large distances | AP Physics 1 | Khan Academy

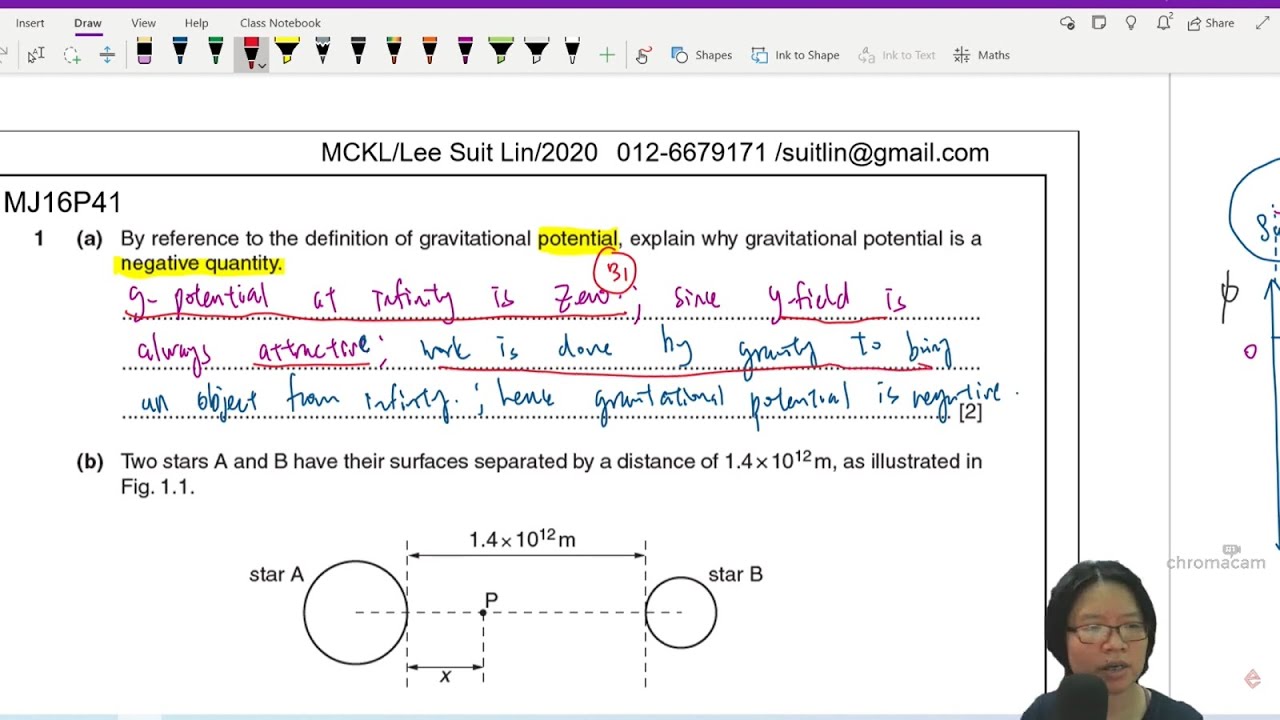
MJ16 P41 Q1 Gravitational Potential Between 2 Stars | A2 G-fields | Cambridge A Level 9702 Physics

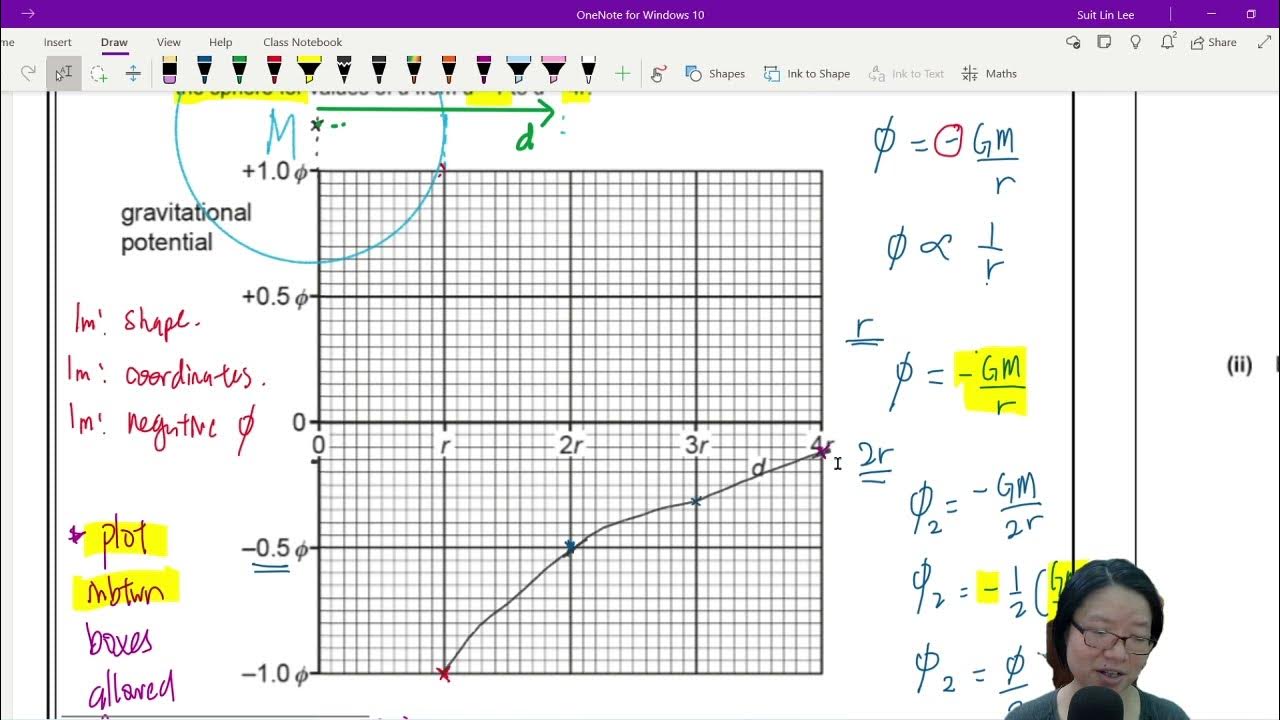
13.3b Ex1 MJ20 P42 Q1 Rock Potential Energy | A2 Gravitational Fields | Cambridge A Level Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsGravitational PotentialPotential EnergyWork CalculationGravitational FieldEnergy ConversionScientific ExplanationEducational ContentMechanics of GravityAstrophysical Processes