Comparison of Series

Chad Gilliland
10 Feb 201413:37
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the concept of series convergence and divergence, focusing on comparison and limit comparison tests. It explains that if a series' terms are smaller than a known convergent series, it too converges; conversely, if terms exceed a known divergent series, it diverges. The script demonstrates how to apply these tests with examples, emphasizing the importance of identifying and comparing the dominant terms, or 'fluff,' to determine a series' behavior. It concludes with a tip to simplify the process by ignoring non-dominant factors and focusing on the most significant powers.

Takeaways
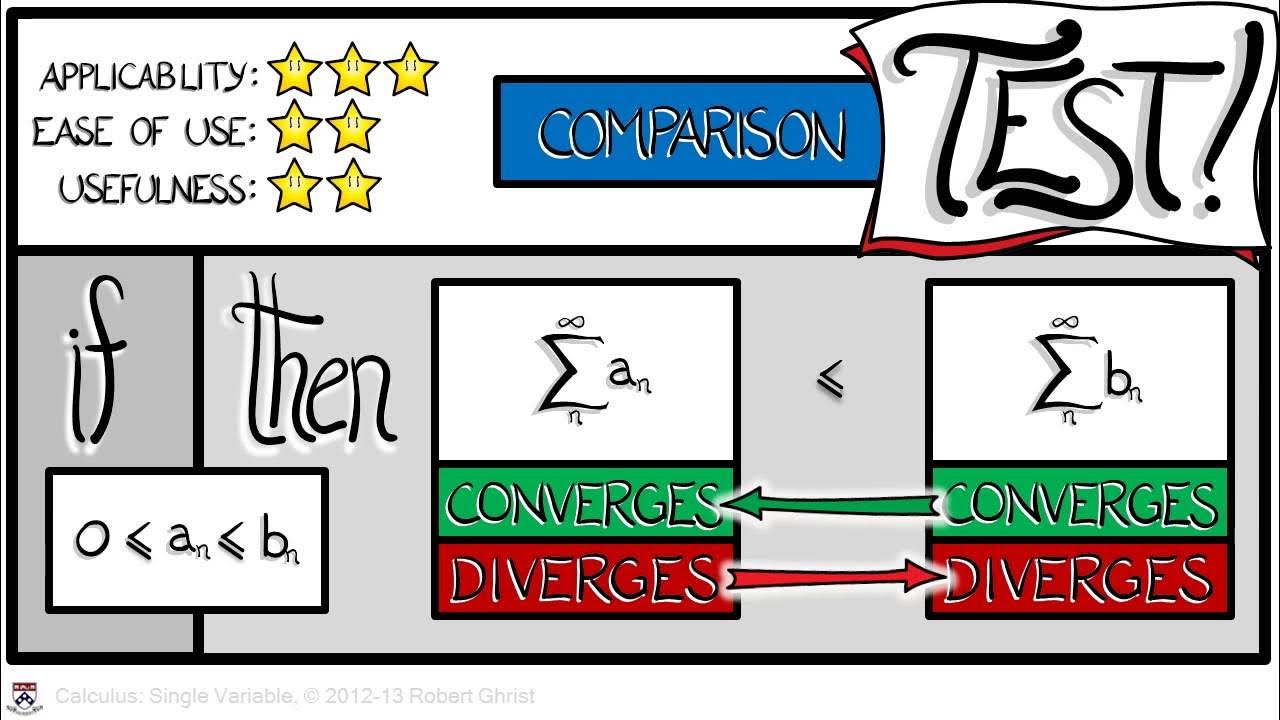
  • 📚 The video discusses methods to determine if a series converges or diverges by comparing it to known series.
  • 🔍 If a series has all positive or zero terms and its terms are smaller than a known convergent series, it also converges.
  • 🔎 Conversely, if a series has terms larger than a known divergent series, it will also diverge.
  • 🌐 The script provides an example comparing the series 1/(n^3 + 1) to the known convergent p-series 1/n^3.
  • 📉 When comparing series, terms should be compared term by term to determine if one series is larger or smaller than the other.
  • 📈 The script introduces the concept of 'fluff' in series terms, which are the parts that do not significantly affect the series' behavior.
  • 🔑 The importance of identifying the largest power in a series for comparison purposes is emphasized.
  • 📝 The limit comparison test is introduced as a method to determine the behavior of series by taking the limit of the ratio of two series' terms as n approaches infinity.
  • 🤔 If the limit is a finite positive number, the series either both converge or both diverge, depending on the behavior of the series used for comparison.
  • 🚫 The script warns that if the limit is not a finite positive number, the comparison series was likely not a suitable choice.
  • 🛑 The video concludes with a reminder to always ignore 'fluff' and focus on the largest power when comparing series for convergence or divergence.
Q & A

  • What is the main purpose of the video script?

    -The main purpose of the video script is to explain how to determine whether a series converges or diverges by comparing it to a known series using the direct comparison test and the limit comparison test.

  • What are the conditions for using the direct comparison test?

    -The conditions for using the direct comparison test are that all terms of the series being tested must be positive or at least zero, and they must be smaller than the corresponding terms of a known convergent series.

  • How does the direct comparison test work when comparing a series to a known divergent series?

    -If all terms of the series being tested are larger than the terms of a known divergent series, then the series being tested must also diverge.

  • What is meant by 'fluff' in the context of the video script?

    -In the context of the video script, 'fluff' refers to the terms or factors in a series that do not significantly affect the overall behavior of the series, such as constant terms or lower order terms.

  • Can you provide an example of how to apply the direct comparison test using the script's content?

    -An example given in the script is the series 1/(n^3 + 1). By comparing it to the known convergent series 1/n^3, and showing that the terms of the given series are smaller, one can conclude that the given series also converges.

  • What is the limit comparison test and when is it used?

    -The limit comparison test is used when you cannot determine the convergence or divergence of a series by direct comparison. It involves dividing one series by another and taking the limit as n approaches infinity. If the limit is a finite positive number, the series either both converge or both diverge.

  • How does the script simplify the comparison process for series?

    -The script suggests simplifying the comparison process by ignoring the 'fluff' and focusing on the largest power of n in the terms of the series, which helps in quickly identifying the behavior of the series.

  • What is the significance of the term 'p-series' mentioned in the script?

    -A 'p-series' is a series of the form 1/n^p, where p is a constant. The script mentions that if p > 1, the p-series is known to converge, which is used as a reference for comparison in some examples.

  • Can you explain the concept of 'geometric series' as mentioned in the script?

    -A geometric series is a series where each term is a constant ratio times the previous term. In the script, it is mentioned that a geometric series with a ratio (r) less than 1 converges, which is used as a known series for comparison.

  • What is the conclusion of the limit comparison test for the series 1/(n^5 + 10n - n^3 + 7) compared to 1/n?

    -The conclusion is that the series 1/(n^5 + 10n - n^3 + 7) is a divergent series because the limit comparison test with 1/n, a known divergent series, results in a finite positive ratio, indicating the behavior of the series is the same as the known series.

Outlines
00:00
📚 Series Convergence and Divergence Tests

This paragraph introduces the concept of series convergence and divergence, focusing on comparison tests. It explains that if a series has terms smaller than a known convergent series, it must also converge. Conversely, if a series has terms larger than a known divergent series, it will diverge. The paragraph uses the example of the summation 1/(n^3 + 1) and compares it to the known convergent p-series 1/n^3, demonstrating that the former also converges because its terms are smaller than the latter's.

05:02
🔍 Direct and Limit Comparison Tests

The second paragraph delves deeper into the comparison tests, illustrating how to apply them with examples. It contrasts the direct comparison test with the limit comparison test, explaining that the latter is used when the series terms do not allow for straightforward comparison. The paragraph provides examples of both tests, including a geometric series with a ratio less than 1, which converges, and a series compared to 1/√n, which diverges. The importance of simplifying the series by removing 'fluff' or insignificant terms is emphasized for easier comparison.

10:03
📉 Applying the Limit Comparison Test

The final paragraph focuses on the limit comparison test, providing a step-by-step guide on its application. It explains how to determine if two series converge or diverge by comparing their terms after removing insignificant factors and taking the limit as n approaches infinity. The paragraph includes an example comparing a series to 1/n^3, which is known to converge, and demonstrates that the given series also converges because it simplifies to a form that is essentially a multiple of the known convergent series. The speaker advises to always ignore 'fluff' and focus on the largest power when applying these tests, especially for quick assessments in multiple-choice questions.

Mindmap
Keywords
💡Convergence
Convergence refers to a series where the sum of its terms approaches a finite number as more terms are added. In the video, it's explained that if a known series converges, any other series with terms smaller than this known series will also converge. For example, the series 1/n^3 is used to illustrate a convergent series.
💡Divergence
Divergence describes a series where the sum of its terms grows indefinitely as more terms are added. The video explains that if a known series diverges, any series with terms larger than this known series will also diverge. Examples such as 1/n and 5/2^n are used to demonstrate divergent series.
💡Comparison Test
The Comparison Test is a method to determine the convergence or divergence of a series by comparing it to another series with known behavior. The video details how comparing terms of a series to those of a known convergent or divergent series helps in concluding the behavior of the new series.
💡P-Series
A P-Series is a series of the form 1/n^p, where 'p' is a positive constant. The video mentions that a P-Series converges if p > 1 and diverges if p ≤ 1. An example given is 1/n^3, which converges because 3 is greater than 1.
💡Geometric Series
A Geometric Series is a series where each term is a constant multiple of the previous term. The video explains that a geometric series converges if the absolute value of the common ratio is less than 1. An example given is (1/3)^n, which converges since 1/3 is less than 1.
💡Limit Comparison Test
The Limit Comparison Test involves dividing terms of two series and taking the limit as n approaches infinity. If the limit is a finite, positive number, both series either converge or diverge together. The video provides examples, such as comparing n^4/(4n^5) with 1/n, to illustrate this concept.
💡Fluff
Fluff refers to terms in a series that do not significantly affect its convergence or divergence. The video advises ignoring fluff to simplify the comparison, focusing on the dominant terms instead. For instance, in the series 1/n^3 + 1, the '+1' is considered fluff.
💡Known Series
A Known Series is a series whose convergence or divergence is already established and can be used for comparison. The video emphasizes the importance of selecting an appropriate known series, such as 1/n or 1/n^3, for applying comparison tests.
💡Terms
Terms are the individual elements of a series that are summed to study its overall behavior. The video discusses comparing terms of different series to determine convergence or divergence. For example, comparing terms like 1/2, 1/9, 1/27 to understand the series' behavior.
💡Finite Number
A Finite Number is a specific, bounded value that a convergent series approaches as the number of terms increases. The video highlights that a series converges if its sum approaches a finite number. For example, a convergent geometric series approaches a finite limit.
Highlights

Introduction to series convergence tests and comparisons.

Requirement for terms in series to be positive or zero for comparison tests.

Explanation of convergence when a series has smaller terms compared to a known convergent series.

Diverges when a series has larger terms compared to a known divergent series.

Demonstration of comparing a series to a known convergent p-series with P=3.

Method of comparing terms directly to determine convergence or divergence.

Comparison of a series to a geometric series with a known convergence property.

Understanding the behavior of a series by comparing it to a known divergent p-series with P=1/2.

Introduction to the limit comparison test for series.

Limit comparison test where the ratio of series terms converges to a finite number.

Simplification technique by ignoring 'fluff' to focus on the significant terms in series comparison.

Application of limit comparison test to determine the behavior of a series when compared to 1/N^3.

Approach to quickly determine series behavior using simplification and comparison.

Final note on the importance of simplifying series for quick analysis in multiple-choice questions.

Transcripts

Browse More Related Video

Direct comparison test | Series | AP Calculus BC | Khan Academy

Tests for Convergence

Calculus BC – 10.6 Comparison Tests for Convergence

Series Tests - Limit Comparison Test

Calculus Chapter 5 Lecture 51 Convergence Tests 1

Estimating Sums Using the Integral Test and Comparison Test

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Series ConvergenceMathematicsTutorialComparison TestLimit ComparisonDivergenceConvergent SeriesDivergent SeriesCalculusEducational Content