Series Tests - Limit Comparison Test

turksvids
14 Oct 201708:55
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial explains the Limit Comparison Test for series convergence, emphasizing its application when both series terms are positive. The test involves comparing the limit of the ratio of consecutive terms as 'n' approaches infinity. If the limit is positive and finite, both series converge or diverge together. The presenter illustrates the process with examples, simplifying complex terms to recognizable series like p-series or geometric series, and using the test to determine convergence or divergence, highlighting the importance of identifying dominant terms and the potential need for additional tests in some cases.

Takeaways
  • 📘 The limit comparison test is used to determine the convergence or divergence of two series.
  • ➗ If given two series, sum of a_n and sum of b_n, with a_n and b_n both greater than zero, calculate the limit as n approaches infinity of a_n/b_n or b_n/a_n.
  • 🔄 If the limit is positive and finite, either both series converge or both series diverge.
  • 🔍 The process involves picking or constructing one of the series based on known behaviors.
  • 🧮 Example: Given the series sum of n(n-3)/(n+2)(n^3-4), simplify to a comparable series for easier analysis.
  • 🎯 Simplification: Ignore constants or minor terms in the numerator and denominator, focusing on dominant terms.
  • ✅ Convergence check: Compare with known convergent series (like a p-series where p > 1).
  • 📏 Take the limit of the original series term divided by the simplified series term, and apply L'Hopital's rule if necessary.
  • 🔗 Consistent results: If the limit equals 1 (positive and finite), the original series behaves like the simplified one.
  • 🧪 Multiple examples illustrate the process of constructing a comparable series and applying the limit comparison test.
Q & A

  • What is the Limit Comparison Test?

    -The Limit Comparison Test is a method used to determine the convergence or divergence of a series by comparing it to another series. If the limit of the ratio of the terms of the two series is positive and finite, then both series either converge or diverge together.

  • What are the conditions for applying the Limit Comparison Test?

    -To apply the Limit Comparison Test, both series a_n and b_n must be greater than zero. The limit of the ratio of a_n to b_n (or vice versa) as n approaches infinity must be positive and finite.

  • What should you do if you take the limit and get a positive finite value?

    -If the limit of the ratio of the terms is positive and finite, then both series will either converge or diverge together. This means you can conclude the behavior of the given series based on the known behavior of the comparison series.

  • What is the key idea behind using the Limit Comparison Test?

    -The key idea is to compare the given series with a known series by constructing a similar series and analyzing the dominant terms. By knowing the behavior of the comparison series, you can infer the behavior of the given series.

  • In the provided example, how is the comparison series constructed?

    -The comparison series is constructed by simplifying the given series to its dominant terms. For instance, n - 3 is approximated as n, and n^3 - 4 is approximated as n^3, leading to a simpler series for comparison.

  • Why do we often end up with a p-series or a geometric series when using the Limit Comparison Test?

    -We often end up with a p-series or a geometric series because these are simpler forms that dominate the behavior of more complex series as n approaches infinity. These forms are well-understood and make it easier to determine convergence or divergence.

  • How do you simplify the given series to a form that can be compared using the Limit Comparison Test?

    -To simplify the given series, focus on the dominant terms in the numerator and denominator. Ignore smaller terms that have less impact as n approaches infinity, and then construct a simpler comparison series using these dominant terms.

  • What happens if the limit of the ratio of the terms is not positive and finite?

    -If the limit of the ratio of the terms is not positive and finite, the Limit Comparison Test is inconclusive. In such cases, you may need to use other tests like the Integral Test or Direct Comparison Test to determine the behavior of the series.

  • Can you provide an example of a series where the Limit Comparison Test is used?

    -Yes, consider the series sum of n(n - 3) / (n + 2)(n^3 - 4). By simplifying to dominant terms, we get n^2 / n^4, which simplifies to 1 / n^2. Comparing this with the p-series 1 / n^2, which converges, we find that the original series also converges.

  • What should you do if the constructed series requires further testing to determine its behavior?

    -If the constructed series requires further testing, you may need to use additional tests such as the Integral Test or Direct Comparison Test. These tests can help confirm the convergence or divergence of the constructed series, allowing you to apply the Limit Comparison Test effectively.

Outlines
00:00
📚 Introduction to the Limit Comparison Test

This paragraph introduces the concept of the limit comparison test, a method used to determine the convergence or divergence of two series. The test involves comparing the ratio of the nth terms of two series as n approaches infinity. If this ratio converges to a positive finite value, both series either converge or diverge together. The speaker emphasizes the importance of constructing or selecting a series that is easier to analyze, typically a p-series, to facilitate the comparison. An example is given where the series involves terms like n(n-3)/(n^3-4), which is simplified to a p-series by focusing on the dominant terms, ultimately concluding that the series converges.

05:00
🔍 Applying the Limit Comparison Test with Examples

The speaker continues by applying the limit comparison test to additional examples. The first example involves a series with terms like n^3 + 8n over the square root of n^7 + 2n^2 + 4. By focusing on the dominant terms, the series is simplified to a form that resembles a p-series, leading to the conclusion that it diverges. The second example features a series with terms like e^n + n over e^(2n) - n^2, which simplifies to a geometric series. The test shows that this series converges. The speaker highlights the importance of identifying the dominant terms in both the numerator and the denominator to construct a series that can be easily analyzed. The method is summarized by noting that the constructed series often ends up being a p-series or a geometric series, which are straightforward to evaluate.

Mindmap
Keywords
💡Limit Comparison Test
The Limit Comparison Test is a method used in calculus to determine whether two series converge or diverge together. It is defined by comparing the limit of the ratio of the nth terms of two series as n approaches infinity. In the video, this test is the central theme, and it is used to analyze the convergence of different series by comparing them to simpler, known series.
💡Series
A series in mathematics is the sum of the terms of a sequence. It is a fundamental concept in calculus and analysis. In the context of the video, series are the main objects of study, with the focus on their convergence or divergence, particularly using the Limit Comparison Test.
💡Convergence
Convergence refers to the property of a series where the sum of its terms approaches a finite limit as the number of terms increases indefinitely. The video discusses how the Limit Comparison Test can be used to determine if a series converges by comparing it to another series with known convergence properties.
💡Divergence
Divergence is the opposite of convergence, indicating that a series does not approach a finite limit as the number of terms increases. The video script explains that if the limit comparison test results in a positive finite value, both series either converge or diverge together.
💡nth Term
The nth term of a series is the term in the sequence that is in the nth position. In the video, the nth term is crucial for the Limit Comparison Test, as the test involves taking the limit of the ratio of the nth terms of two series.
💡P-Series
A P-Series, or a power series, is a type of series where the terms are of the form 1/n^p, where p is a constant. In the video, P-Series are mentioned as a common type of series that can be easily compared using the Limit Comparison Test, as they have a well-known convergence behavior.
💡Limit
In mathematics, a limit describes the behavior of a function or sequence as the input approaches a certain value. The video script repeatedly refers to the concept of limits, particularly when explaining how to apply the Limit Comparison Test by calculating the limit of a ratio of terms.
💡Dominant Term
The dominant term in a series or expression is the term that has the most significant impact on the overall value as the variables involved approach infinity. In the script, the concept of dominant terms is used to simplify series for the purpose of the Limit Comparison Test by focusing on the terms that will ultimately determine the behavior of the series.
💡L'Hôpital's Rule
L'Hôpital's Rule is a technique in calculus for finding the limit of a quotient of two functions when the limit would otherwise be indeterminate. In the video, the presenter mentions using L'Hôpital's Rule to simplify the process of taking limits in the context of the Limit Comparison Test.
💡Geometric Series
A geometric series is a series where each term after the first is found by multiplying the previous one by a constant called the common ratio. The video script includes an example where a series is compared to a geometric series to determine its convergence using the Limit Comparison Test.
Highlights

The Limit Comparison Test is introduced for determining the convergence of two series.

The test requires that both series terms are greater than zero.

Calculation of the limit as n approaches infinity of the ratio of corresponding terms is essential.

A positive finite limit implies both series converge or diverge together.

The importance of constructing or selecting one of the series for comparison is emphasized.

Example provided with series involving n, n^2, and n^3 terms.

Simplification of terms to identify a p-series for comparison.

Explanation of how to determine if a p-series converges based on its value.

Demonstration of taking the limit using the constructed series.

Use of L'Hôpital's rule for simplifying limits in series comparison.

Result of the limit indicating the convergence of the original series.

Second example with a series that resembles a p-series with additional terms.

Focusing on the dominant terms to construct a comparable series.

Identification of a divergent p-series and its impact on the given series.

Third example involving a series with exponential and polynomial terms.

Comparison with a geometric series and its convergence properties.

Final conclusion based on the limit comparison test for the given series.

Advice on constructing a series based on dominant terms for easier comparison.

Mention of potential need for additional tests on the constructed series.

Transcripts

Browse More Related Video

Worked example: limit comparison test | Series | AP Calculus BC | Khan Academy

AP Calculus BC Lesson 10.6 Part 2

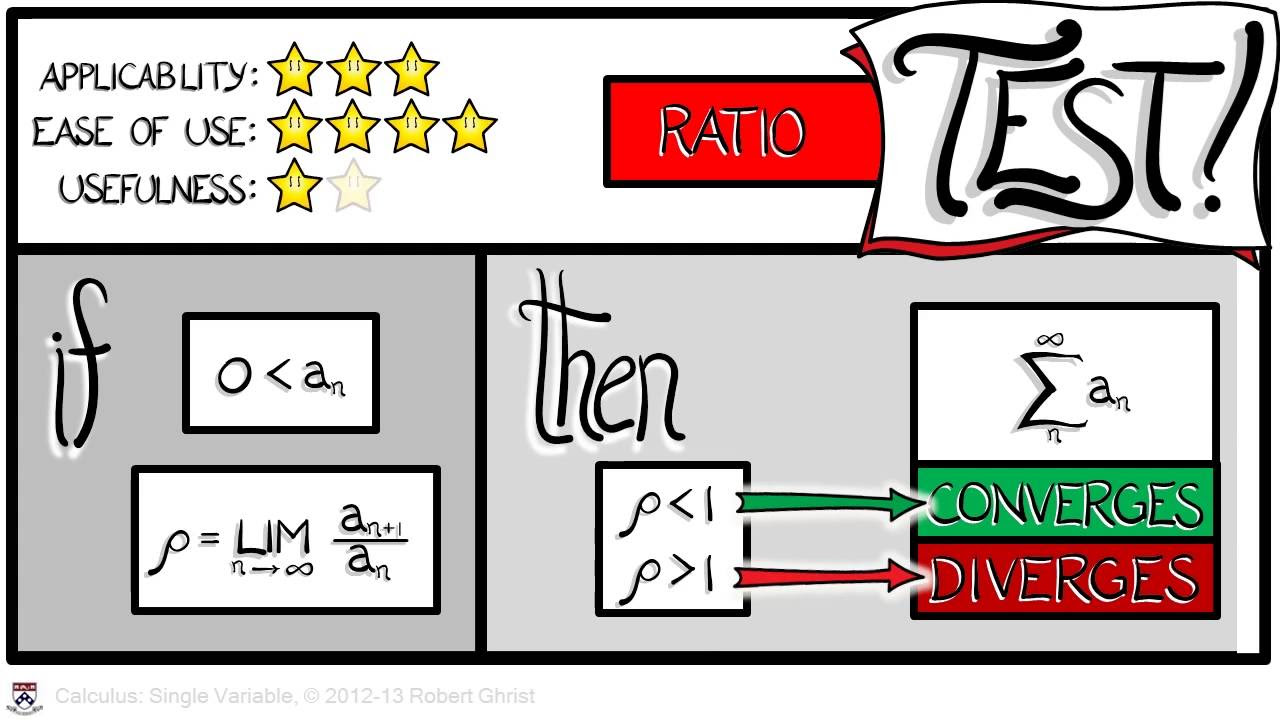
Calculus Chapter 5 Lecture 52 Convergence Tests 2

Worked example: interval of convergence | Series | AP Calculus BC | Khan Academy

Infinite Series Multiple Choice Practice for Calc BC (Part 2)

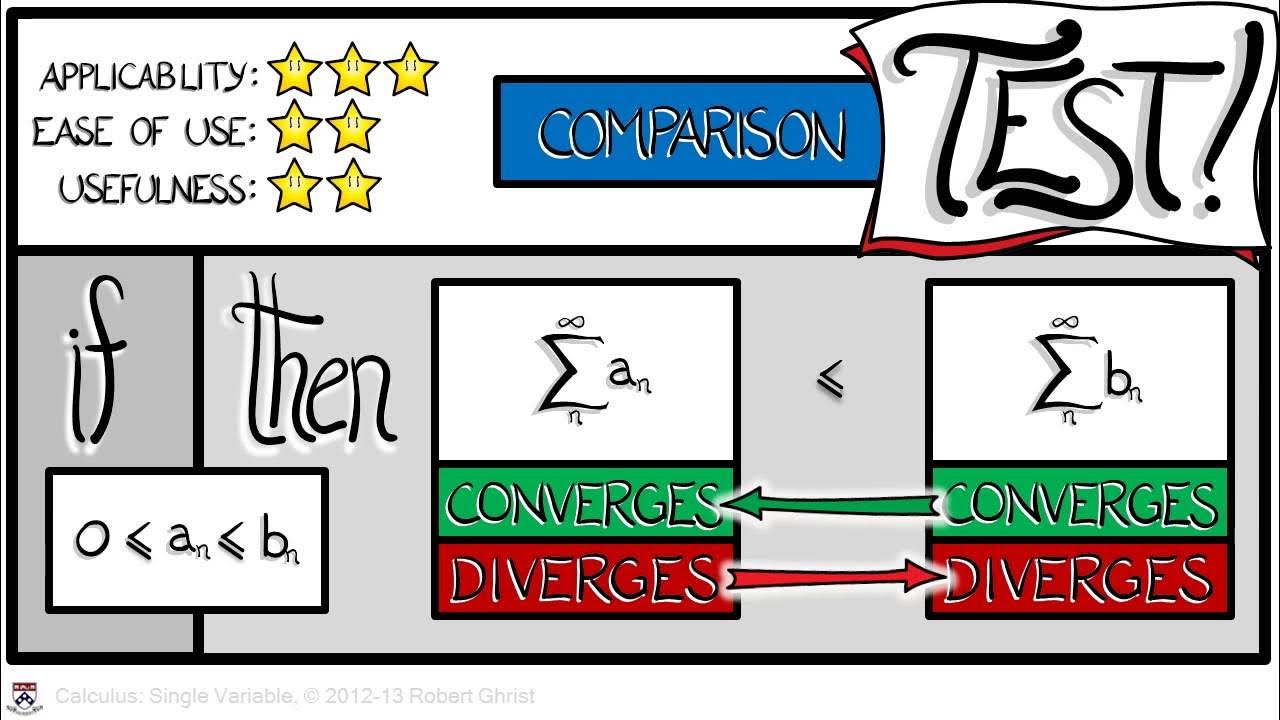
Calculus Chapter 5 Lecture 51 Convergence Tests 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Limit Comparison TestSeries ConvergenceMathematics TutorialCalculus TechniquesEducational ContentP-Series AnalysisGeometric SeriesL'Hopital's RuleConvergence CriteriaMathematical Examples