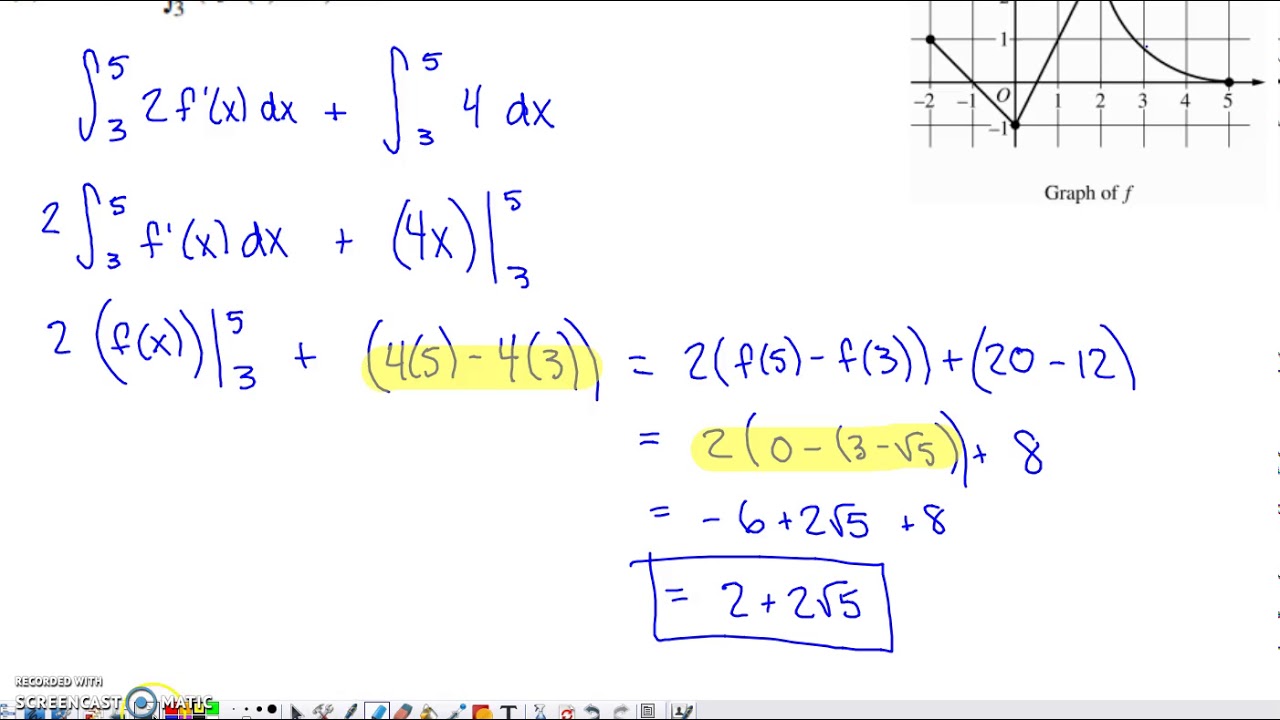
Justifying our Answers on Improper Integrals
TLDRIn this educational video, the presenter addresses a common issue students face when evaluating improper integrals. They explain why simply applying the Fundamental Theorem of Calculus may not yield full credit, especially when dealing with functions like 1/x^2 that have discontinuities. The video emphasizes the importance of using limits to properly justify answers for improper integrals, illustrating the process with the example of 1/x^4 from 0 to 1. It highlights the necessity of transforming the integral into a limit to ensure correct evaluation and to avoid losing points on exams like the AP Calculus.
Takeaways
- 📚 The fundamental theorem of calculus is crucial for understanding integrals, stating that the integral from A to B of a continuous function f'(x) is f(B) - f(A).
- 🔍 Improper integrals, such as y = 1/x^2, require special attention because they involve discontinuities or infinite values.
- 🤔 The issue with improper integrals arises when the function is not continuous over the entire interval, as seen with y = 1/x^2, which is discontinuous at x = 0.
- 📊 The graph of the anti-derivative of y = 1/x^2 shows an infinite increase at x = 0, indicating an infinite area under the curve, not a finite value like -2.
- 🚫 The fundamental theorem of calculus cannot be directly applied to improper integrals due to the discontinuity at certain points.
- 🔄 To handle improper integrals, the integral must be split into separate pieces at the points of discontinuity, such as from -1 to 0 and 0 to 1 for y = 1/x^2.
- 💡 The concept of limits is essential in evaluating improper integrals, as it allows for the calculation of the area under the curve by approaching the discontinuity.
- 📘 When solving improper integrals, one must take the limit of the definite integral as one of the bounds approaches the point of discontinuity.
- 🎓 In the context of AP Calculus, credit is not awarded for improper integral questions unless a limit is used in the solution process.
- 👨🏫 The video emphasizes the importance of transforming an improper integral into a limit to ensure proper evaluation and credit in academic assessments.
Q & A
What is the main topic of the video?
-The main topic of the video is justifying answers on improper integrals and discussing why some students might have received little credit on a particular question, even if they got the answer right.
What is the fundamental theorem of calculus mentioned in the video?
-The fundamental theorem of calculus states that if a function 'f' is continuous on the closed interval [A, B], then the integral from A to B of f'(x) dx is equal to f(B) minus f(A), where 'f' is the antiderivative of 'f'(x).
Why is the integral of y = 1/x^2 from -1 to 1 not equal to -2?
-The integral of y = 1/x^2 from -1 to 1 is not equal to -2 because the antiderivative of 1/x^2 is discontinuous at x = 0, which is a vertical asymptote, and the integral actually diverges to infinity, not a finite value.
What is the issue with using the fundamental theorem of calculus on the integral of y = 1/x^2 from -1 to 1?
-The issue is that the fundamental theorem of calculus cannot be applied directly to this integral because the function is not continuous over the entire interval due to the discontinuity at x = 0.
How should the integral of y = 1/x^2 from -1 to 1 be approached correctly?
-The integral should be approached by considering the improper nature of the integral and using limits to evaluate the area under the curve, rather than directly applying the fundamental theorem of calculus.
What is the significance of the discontinuity at x = 0 in the context of the integral of y = 1/x^2?
-The discontinuity at x = 0 is significant because it indicates that the function is not defined at that point, and the integral over this interval diverges to infinity, which is not captured by simply finding an antiderivative and evaluating it at the bounds.
Why is it incorrect to plug in the value of x = 0 directly into the antiderivative of x^(-2)?
-It is incorrect because plugging in x = 0 directly would result in an indeterminate form (0^(-2)), and the actual behavior of the function near x = 0 is that it approaches infinity, which is not represented by the antiderivative evaluated at zero.
What is the correct approach to evaluate the improper integral from 0 to 1 of x^(-4/5) dx?
-The correct approach is to take the limit of the definite integral as the lower bound approaches the point of discontinuity, which in this case is x = 0, and then evaluate the limit to find the value of the improper integral.
Why is it crucial to use a limit when evaluating an improper integral in an exam setting?
-Using a limit is crucial because it accurately reflects the behavior of the function near points of discontinuity and is a requirement for proper credit in exams like AP Calculus, where the fundamental theorem of calculus cannot be applied directly.
What is the common mistake made by students when solving improper integrals as described in the video?
-The common mistake is not transforming the improper integral into a limit expression, which is necessary to accurately evaluate the integral and receive full credit in an exam setting.
Outlines
📚 Understanding Improper Integrals and Their Justification
The video begins by addressing a common concern about receiving low credit on a question involving improper integrals, despite the correct answer. The presenter reminds viewers of the fundamental theorem of calculus, which states that the integral of a continuous function over a closed interval can be calculated by finding the anti-derivative and evaluating it at the interval's endpoints. However, this theorem does not apply to improper integrals, such as y = 1/x^2, which are not continuous over their entire domain. The video demonstrates the incorrectness of using the fundamental theorem on such integrals by showing the area under the graph between -1 and 1, which should be positive but is incorrectly calculated as -2. The presenter emphasizes the importance of recognizing discontinuities, such as the vertical asymptote at x = 0, and explains that improper integrals must be handled by splitting the integral and taking limits as the bounds approach the discontinuity.
🔍 Correct Approach to Improper Integrals Using Limits
Continuing from the previous explanation, the video delves into the correct method for evaluating improper integrals. The presenter clarifies that the fundamental theorem of calculus cannot be directly applied to functions with vertical asymptotes, such as x^(-2), without considering the discontinuity. Instead, the integral must be transformed into a limit expression, where the troublesome point (e.g., x = 0) is approached as a limit. The video uses an example of an improper integral from 0 to 1 of x^(4/5) dx to illustrate this process. The presenter explains that the anti-derivative is found as usual, but the value at the discontinuity (x = 0) must be approached by taking the limit. This approach is crucial for receiving full credit on problems involving improper integrals, as it ensures that the discontinuity is properly accounted for. The video concludes by reiterating the importance of this method and the potential for losing credit if the limit is not used in the solution.
Mindmap
Keywords
💡Improper Integrals
💡Fundamental Theorem of Calculus
💡Antiderivatives
💡Continuous Function
💡Vertical Asymptote
💡Limit
💡Divergence
💡Integral Bounds
💡Free Response
💡Credit in Exams
💡AP Calculus
Highlights
The video discusses justifying answers on improper integrals and addressing the issue of receiving little credit despite correct answers.
The fundamental theorem of calculus is introduced, explaining its application to continuous functions on closed intervals.
The concept of improper integrals is introduced with the example of y = 1/x^2, highlighting the issue with the discontinuity at x = 0.
The importance of the anti-derivative's behavior at points of discontinuity is emphasized, especially in relation to the improper integral.
A graphical representation of the anti-derivative of y = 1/x is discussed to illustrate the behavior around discontinuities.
The incorrect result of -2 for the integral from -1 to 1 of y = 1/x^2 is presented, pointing out the mistake due to the discontinuity.
The correct approach to solving improper integrals is outlined, which involves taking the limit as the bounds approach the point of discontinuity.
The video explains why the fundamental theorem of calculus cannot be directly applied to improper integrals due to the presence of discontinuities.
An example of an improper integral with x^(-4/5) is given to demonstrate the correct method of solving such problems.
The necessity of using a limit in the solution process for improper integrals is stressed to ensure proper credit in assessments.
The video clarifies that the anti-derivative alone is not sufficient for full credit on an improper integral question.
A step-by-step guide is provided on how to properly evaluate the limit for an improper integral, including plugging in the value causing the discontinuity.
The importance of transforming an improper integral into a limit to receive full credit is reiterated, especially in the context of AP Calculus exams.
The video concludes by summarizing the key points and emphasizing the importance of correctly justifying answers on improper integrals.
A call to action for viewers to understand and apply the concepts discussed to avoid losing credit on similar problems in the future.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: