Tips to verifying trigonometric identities
TLDRThe video script focuses on the process of verifying trigonometric identities, emphasizing the importance of simplifying one side of the identity to make the comparison easier. The speaker suggests starting with the more complex side, applying operations such as addition, subtraction, multiplication, and factoring, particularly focusing on converting rational expressions to have a monomial denominator. The next step involves applying fundamental trigonometric identities, including quotient, reciprocal, and Pythagorean identities, to further simplify the expression. If progress stalls, the speaker recommends converting all terms to sines and cosines as a last resort. The key message is to keep trying different operations and identities until the desired simplification is achieved, encouraging a proactive approach to problem-solving.
Takeaways
- 📐 **Simplifying vs. Verifying**: The focus shifts from simplifying trigonometric identities to verifying them by ensuring both sides of an identity are equal.
- 🔍 **Choosing a Side**: When starting, pick the side that appears more complex, often involving more operations or terms, to simplify first.
- ➕➖ **Apply Operations**: Perform addition, subtraction, multiplication, and consider factoring, especially when dealing with rational expressions.
- 📉 **Monomial Denominators**: Aim to simplify rational expressions to have a single term in the denominator for easier handling.
- 🔄 **Fundamental Identities**: Utilize quotient, reciprocal, and Pythagorean identities to further simplify expressions.
- 🔀 **Converting Identities**: Use identities to transform expressions, potentially by multiplying or dividing terms to make them more manageable.
- 🧲 **Pythagorean Power**: Recognize when to apply Pythagorean identities, especially when you see squared trigonometric terms.
- 📈 **Progress Over Perfection**: Accept that you may not reach the final form immediately; the goal is to make progress with each step.
- 🔃 **Convert to Sines and Cosines**: As a last resort, convert all terms to sines and cosines if you're stuck, as this can unify the expression.
- 🤔 **Try Something**: If you're unsure what to do next, try an operation or identity application; sometimes the process of elimination can guide you.
- 🔍 **Persistence Pays**: Even if you don't immediately succeed, keep trying different approaches until you find the one that works.
Q & A
What is the main focus of the transcript provided?
-The main focus of the transcript is on verifying trigonometric identities by simplifying one side of the identity and applying various mathematical operations and identities.
Why is it recommended to start with the more complicated side when verifying a trigonometric identity?
-Starting with the more complicated side allows for a more straightforward approach to simplification, as it often involves more operations and terms, making it easier to identify where to apply mathematical techniques.
What are some of the operations that can be applied when simplifying a trigonometric identity?
-Some of the operations that can be applied include addition, subtraction, multiplication, factoring, and converting rational expressions to have a monomial denominator.
What are fundamental identities in the context of trigonometry?
-Fundamental identities in trigonometry include quotient identities, reciprocal identities, and Pythagorean identities, which are essential for simplifying and verifying trigonometric expressions.
How can Pythagorean identities be used in the process of verifying a trigonometric identity?
-Pythagorean identities can be used to convert squared trigonometric terms, which is helpful when dealing with expressions that involve both sine and cosine functions.
What is the suggested approach when one gets stuck while verifying a trigonometric identity?
-When stuck, the speaker suggests converting all terms to sines and cosines, as this can often provide a new perspective and simplify the problem.
Why is it important to try different operations or identities even if it's not clear which one to apply?
-Trying different operations or identities can lead to progress in simplifying the expression. Even if the first attempt doesn't lead to the desired result, it can provide insights that guide the next steps.
What does the speaker mean by 'converting to a monomial denominator' in the context of rational expressions?
-Converting to a monomial denominator refers to simplifying a rational expression so that the denominator is a single term, rather than a more complex expression, which can make further simplification easier.
What is the significance of applying quotient and reciprocal identities in verifying trigonometric identities?
-Quotient and reciprocal identities are used to express one trigonometric function in terms of another, which can simplify the expression and make it easier to see if the two sides of the identity are equivalent.
How does the process of verifying trigonometric identities help in understanding the relationships between different trigonometric functions?
-Verifying trigonometric identities involves manipulating and simplifying expressions, which reinforces the understanding of how different trigonometric functions are related and can be transformed into one another.
What is the role of practice in mastering the process of verifying trigonometric identities?
-Practice is crucial as it allows individuals to become familiar with the various operations and identities, and to develop a sense of which techniques are most effective for different types of problems.
Why is it recommended to focus on one side of the identity first when verifying trigonometric identities?
-Focusing on one side first simplifies the problem and makes it more manageable. It allows for a step-by-step approach, where after simplifying one side, the focus can shift to the other side for comparison.
Outlines
📚 Simplifying and Verifying Trigonometric Identities
The paragraph introduces the process of verifying trigonometric identities, emphasizing the importance of ensuring both sides of an identity are equal. It suggests starting with the more complex side and applying operations such as addition, subtraction, multiplication, and factoring. The speaker also highlights the use of fundamental trigonometric identities like quotient, reciprocal, and Pythagorean identities to simplify expressions further. If stuck, the advice is to convert all terms to sines and cosines, which can often resolve complications in the problem-solving process.
🤔 Overcoming Challenges in Trigonometric Problem Solving
This paragraph addresses the common issue of students getting stuck during the problem-solving process. It encourages students to keep trying different operations or identities to make progress, even if it's not immediately clear which approach will work. The key message is to maintain persistence and to not be afraid to experiment with various strategies until the correct path forward is found.
Mindmap
Keywords
💡Trigonometric Identities
💡Simplifying
💡Equal Side
💡Operations
💡Fundamental Identities
💡Quotient Identities
💡Reciprocal Identities
💡Pythagorean Identities
💡Rational Expression
💡Monomial Denominator
💡Converting Terms
💡Try Something
Highlights
The focus is on verifying trigonometric identities by ensuring both sides are equal.
Select the most complicated side to simplify first.
Apply operations such as addition, subtraction, multiplication, and factoring.
Convert rational expressions to have a monomial denominator.
There is no one-size-fits-all approach; try different operations and identities.
Apply fundamental trigonometric identities like quotient, reciprocal, and Pythagorean.
Use quotient identities for conversions and to simplify multiplication or division.
Convert any trigonometric term squared using Pythagorean identities.
If stuck, convert all terms to sines and cosines.
Persistence is key; always try an operation or identity even if unsure.
The process involves simplifying, applying operations, using identities, and converting terms.
Starting with the most complex side can streamline the verification process.
Factoring is particularly useful when dealing with rational expressions.
The ability to apply identities is crucial for simplifying trigonometric expressions.
When all else fails, converting to sines and cosines can provide a new perspective.
The approach encourages a flexible and iterative method to problem-solving.
Students are encouraged to try different strategies and learn from each attempt.
The method aims to equip students with a comprehensive toolkit for identity verification.
Transcripts
Browse More Related Video

Introduction to Using Trigonometric Identities (Precalculus - Trigonometry 23)

Precalc 5.2 Verifying Trig Identities
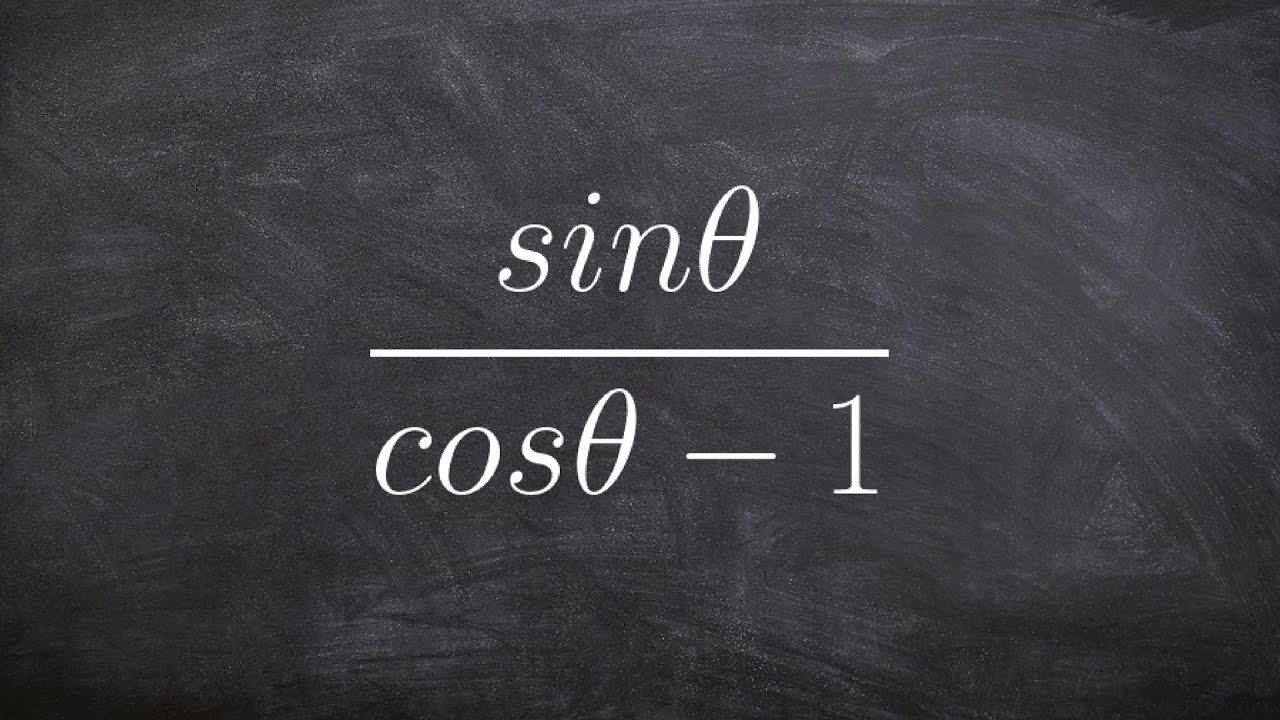
How do you simplify trigonometric expressions
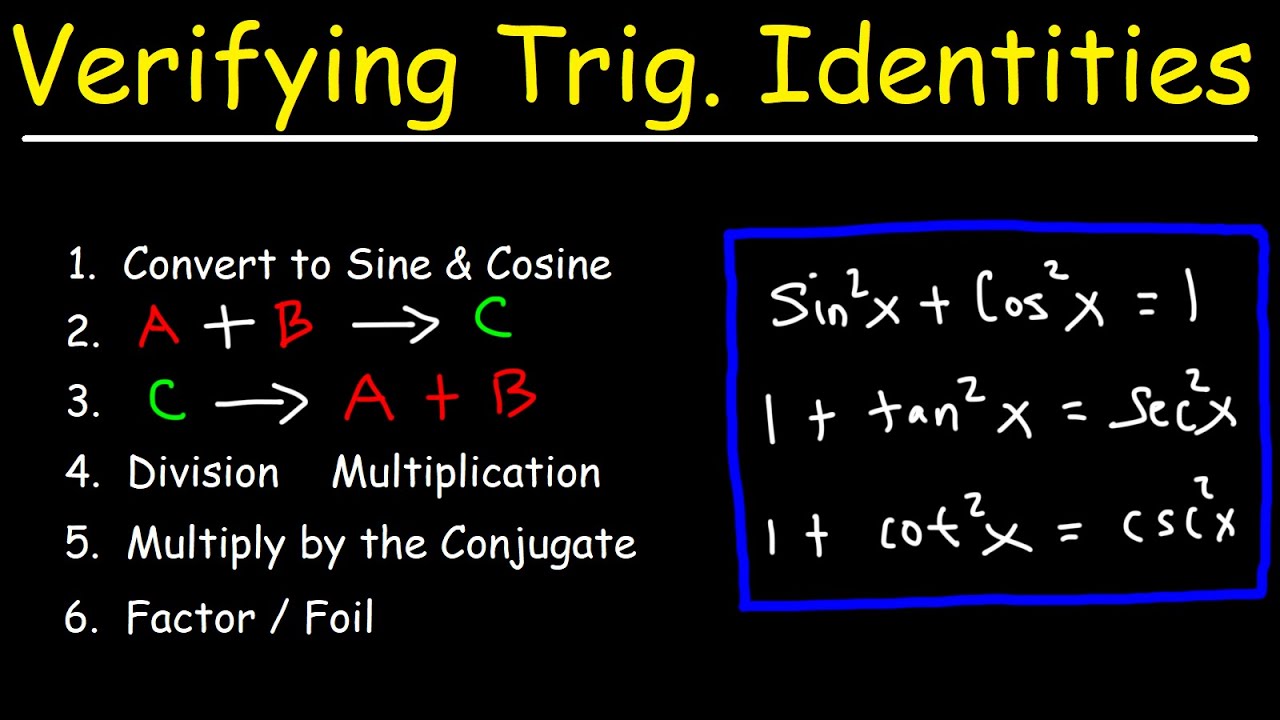
Verifying Trigonometric Identities

How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)

Identities Grade 11: Introduction and practice
5.0 / 5 (0 votes)
Thanks for rating: