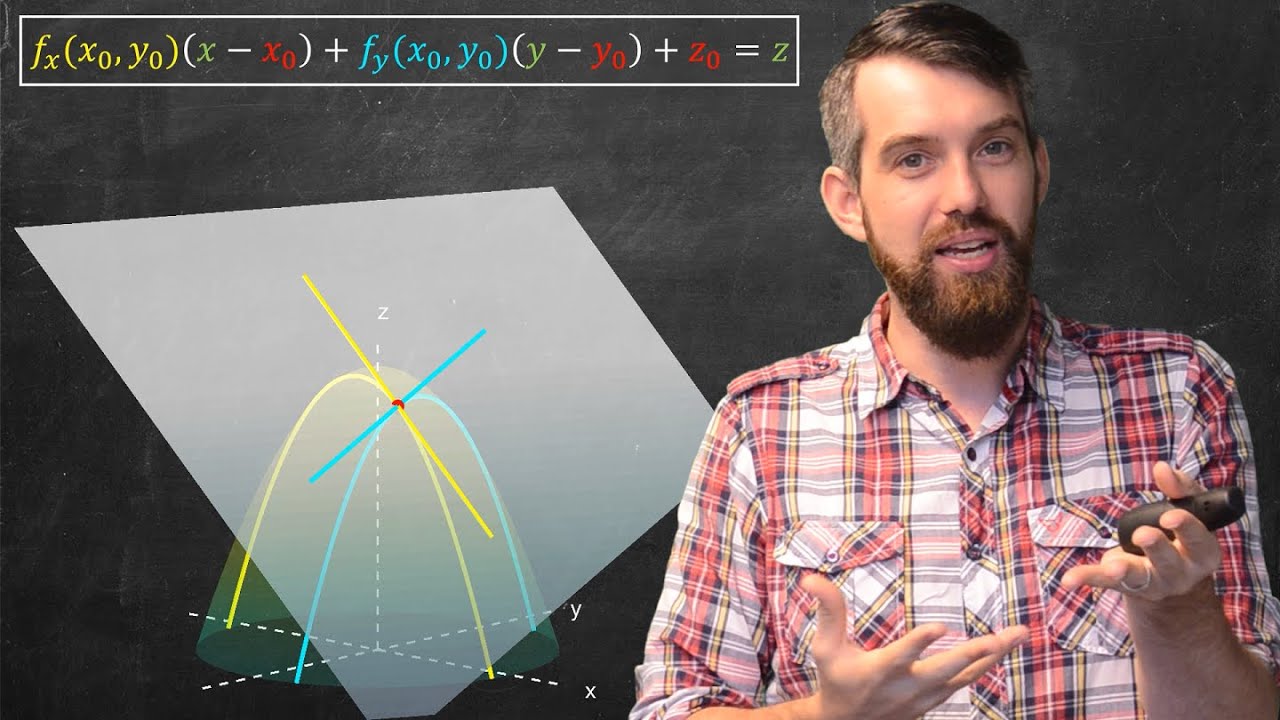
Controlling a plane in space
TLDRThis educational video script explains the concept of finding the tangent plane to a graph in three dimensions. It starts by illustrating how planes are controlled in 3D space, using a red dot to represent a point with coordinates (1, 2, 3). The script then introduces the function 'l' that models the plane's graph, emphasizing the need to distinguish it from other planes passing through the same point. It explains the constant slope of planes in any direction, which is derived from the partial derivatives of 'l' with respect to x and y. The video concludes by constructing the function 'l' using the given point and slopes, highlighting the importance of understanding partial derivatives for controlling the function's behavior at any point.
Takeaways
- 🔴 To find the tangent plane to a graph, first understand how planes are controlled in three dimensions.
- 🔵 A point in three dimensions has coordinates (1, 2, 3) for x, y, and z respectively.
- 📐 Many planes can pass through a single point, but we need to distinguish the specific plane we're examining using partial derivatives.
- 📊 The graph of the function should pass through the point (1, 2, 3), meaning l(1, 2) = 3.
- 🔀 A key property of planes is that intersecting with another plane yields a straight line, indicating a constant slope in the direction of intersection.
- 🧮 The partial derivative of l with respect to x is a constant (a), and the partial derivative with respect to y is another constant (b).
- 🔍 Estimating slopes: for the x direction, the slope is about 2; for the y direction, it's about 1.
- 📏 The function l(x, y) can be represented as a linear combination of x and y, with constants determined by partial derivatives.
- 🔄 Adjusting the function form by shifting constants to simplify evaluation at the point (1, 2) makes calculations easier.
- 💡 The final function l(x, y) = 2(x - 1) + 1(y - 2) + 3, provides a powerful way to control the plane's slopes and the specific point it passes through.
Q & A
What is the main topic of the video script?
-The main topic of the video script is how to find the tangent plane to a graph in three dimensions.
What is the initial step in finding the tangent plane according to the script?
-The initial step is to understand how to control planes in three dimensions.
What does the red dot in the script represent?
-The red dot represents a point in three-dimensional space with coordinates (1, 2, 3).
What is the function 'l' in the context of the script?
-The function 'l' is a two-dimensional input function (x and y) that represents the graph of the plane.
Why are there many different planes that could pass through a given point?
-There are many different planes that could pass through a given point because they can have various angles and directions.
What property of the graph indicates that it passes through the point (1, 2, 3)?
-The property that the graph passes through the point (1, 2, 3) means that when the function 'l' is evaluated at x=1 and y=2, it should equal z=3.
How does the script describe the intersection of a plane with another plane?
-The script describes the intersection of a plane with another plane as a straight line with a constant slope, indicating the planes are flat and not curvy.
What do the partial derivatives of the function 'l' with respect to x and y represent geometrically?
-The partial derivatives of the function 'l' with respect to x and y represent the constant slopes of the plane in the x and y directions, respectively.
Why are the partial derivatives of 'l' considered to be constant values in the script?
-The partial derivatives are considered constant values because the slopes of the plane do not change as you move in the x or y direction.
How does the script suggest determining the specific plane from other possible planes through the same point?
-The script suggests using partial derivatives to distinguish the specific plane from other possible planes that pass through the same point.
What is the significance of the constants 'a' and 'b' in the script?
-The constants 'a' and 'b' represent the constant slopes of the tangent plane in the x and y directions, respectively.
How does the script suggest finding the function 'l' that represents the tangent plane?
-The script suggests using the values of the function at a specific point, and its partial derivatives with respect to x and y, to determine the function 'l'.
What is the role of the constant 'c' in the function 'l' as described in the script?
-The constant 'c' in the function 'l' represents the vertical shift of the plane, which is determined by evaluating the function at the given point (1, 2) and ensuring it equals the z-coordinate, which is 3.
Why does the script suggest rewriting the function 'l' with terms (x-1) and (y-2)?
-Rewriting the function 'l' with terms (x-1) and (y-2) simplifies the evaluation of the function at the point (1, 2), making it easier to solve for the constant 'k'.
What is the final form of the function 'l' that the script arrives at, and why is it powerful?
-The final form of the function 'l' is l(x, y) = 2(x-1) + 1(y-2) + 3, which is powerful because it allows for control over the slopes in the x and y directions and specifies the exact point the plane passes through.
Outlines
📚 Introduction to Finding Tangent Planes
This paragraph introduces the concept of finding the tangent plane to a graph in three dimensions. It begins with a visual representation of a point with coordinates (1, 2, 3) and a plane passing through it. The objective is to find a function 'l' that represents the plane's graph. The paragraph discusses the challenge of identifying the specific plane among many that could pass through the given point and hints at the use of partial derivatives to solve this problem. It also emphasizes the importance of understanding the properties of planes, such as their constant slope in any direction, and how this relates to the partial derivatives of the function.
🔍 Deriving the Tangent Plane Equation
The second paragraph delves into the process of deriving the equation of the tangent plane. It explains that the partial derivatives of the function 'l' with respect to 'x' and 'y' are constants, which represent the slopes of the plane in the respective directions. The paragraph provides an example of how to use these derivatives to construct the function 'l', starting with the linear terms 2x and y, which correspond to the slopes in the x and y directions. It then introduces a constant 'c' to account for the plane's position in space. The paragraph concludes by showing how to uniquely determine the constant 'c' by evaluating the function at the given point (1, 2) and ensuring it equals the z-coordinate, which is 3.
🛠 Adjusting Plane Equation Parameters
The final paragraph discusses the flexibility in adjusting the parameters of the tangent plane equation to represent different planes passing through the same point. It suggests 'dialing the knobs' of the coefficients in front of 'x' and 'y' to change the slopes and thus the orientation of the plane. The paragraph also explains how to modify the constant term in the equation to ensure that the function evaluates to the correct z-value at the specified point. The goal is to provide a general form of the function that can be easily adjusted for different scenarios, emphasizing the power and utility of this approach for understanding and manipulating planes in three-dimensional space.
Mindmap
Keywords
💡Tangent Plane
💡Three Dimensions
💡Partial Derivatives
💡Graph
💡Slope
💡Intersect
💡Constant Plane
💡Function
💡Linear
💡Coordinate System
💡Equation
Highlights
Introduction to the concept of finding the tangent plane to a graph in three dimensions.
Explanation of how to control planes in three-dimensional space using a red dot representing a point with coordinates (1, 2, 3).
Discussion on the multitude of planes that can pass through a single point and the need to distinguish the specific one of interest.
Introduction of function 'l' that represents the plane's graph with two-dimensional input (x, y).
Observation that the graph of the plane passes through the point (1, 2, 3) and its implications for the function 'l'.
Analysis of the properties of planes and their intersections with other planes, resulting in constant slopes.
Introduction of the concept of partial derivatives to distinguish the specific plane from other possible planes.
Geometric interpretation of the partial derivative of 'l' with respect to x, represented as a constant 'a'.
Similar geometric interpretation for the partial derivative of 'l' with respect to y, represented as a constant 'b'.
Explanation of how the partial derivatives give control over the function's behavior at all input points for movement in specified directions.
Estimation of the slope of the plane when intersected with a constant y value, suggesting a slope of approximately 2.
Estimation of the slope when intersected with a constant x value, suggesting a slope of approximately 1.
Use of the function's value at the point (1, 2) and its partial derivatives to deduce the form of the function 'l'.
Derivation of the function 'l' as a linear combination of x and y with constants, based on the partial derivatives.
Identification of 'c' as a constant term in the function 'l' that needs to be determined.
Method to determine the constant 'c' by evaluating the function at the point (1, 2) and setting it equal to 3.
Reformulation of the function 'l' to simplify evaluation at the point (1, 2) by introducing constants k.
Conclusion that the constant k should equal 3 to satisfy the condition of the function at the point (1, 2, 3).
Emphasis on the power of the derived function form to control the slopes in both x and y directions.
Encouragement to remember the method of specifying a point and tweaking slopes for future applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: