What is differentiability for multivariable functions??

Dr. Trefor Bazett

17 Jun 202014:35

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the concept of differentiability for multivariable functions by revisiting single-variable calculus. It explains the traditional definition of a derivative and its geometric interpretation as a secant line's slope approaching a tangent line. The script then introduces an alternative perspective using error terms to approximate the function's change. Applying this approach to multivariable functions, it defines differentiability through partial derivatives and error terms, illustrating the process with an example of a discontinuous function with existing partial derivatives. The video concludes by highlighting the importance of partial derivatives and a theorem that links their continuity to function differentiability.

Takeaways

📚 The video revisits the concept of differentiability in single-variable calculus to build intuition before tackling multivariable functions.
🔍 It explains the definition of a derivative as a limit involving a difference quotient, which represents the slope of a secant line between two points on a graph.
📈 The script illustrates the geometric interpretation of differentiability, showing how a tangent line is the limit of secant lines as the points approach each other.
🤔 The video introduces an alternative perspective on differentiability by considering the error term in the approximation of the function's change by its derivative.
📐 The concept of partial derivatives is explored, highlighting their similarity to single-variable derivatives by fixing one variable and analyzing the function with respect to the other.
📉 The script discusses the limitations of partial derivatives, noting that their existence does not necessarily imply full differentiability, as seen in the example of a discontinuous function with existing partial derivatives.
🔄 The definition of multivariable differentiability is presented, requiring that the error terms from the approximations of changes in multiple variables both approach zero as those variables approach zero.
📘 An example is used to demonstrate how a function with existing partial derivatives can fail the test for differentiability, thus resolving the tension between partial derivatives and true differentiability.
🔑 The video emphasizes the importance of continuous partial derivatives, stating that if they exist and are continuous over an open region, the function is guaranteed to be differentiable there.
🛑 The script concludes by reinforcing the utility of partial derivatives in establishing differentiability, except in rare cases where they exist without the function being differentiable.
👍 The video encourages viewer engagement by asking for likes and questions in the comments, indicating a community aspect to the mathematical exploration.

Q & A

What is the main objective of the video regarding differentiability in multi-variable functions?
-The main objective of the video is to explore differentiability for multi-variable functions by looking back at single-variable calculus to understand the problems differentiability was trying to solve and apply similar solutions to higher dimensions.
Why are partial derivatives alone not sufficient to define differentiability in multi-variable functions?
-Partial derivatives alone are not sufficient to define differentiability because they only consider changes in one direction at a time and do not account for the combined effect of changes in multiple directions simultaneously.
How is the derivative of a single-variable function defined?
-The derivative of a single-variable function at a point \( x_0 \) is defined as the limit of the difference quotient as \( h \) approaches 0: \( \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \). This represents the slope of the tangent line to the function at \( x_0 \).
What is the geometric interpretation of the difference quotient in single-variable calculus?
-The difference quotient represents the slope of the secant line between two points on the function, and as the two points get closer together, the slope of the secant line approaches the slope of the tangent line.
What is the new perspective on differentiability presented in the video?
-The new perspective on differentiability involves rewriting the difference quotient with an error term that goes to zero as \( h \) approaches zero. This emphasizes approximating the change in the function value with the derivative and considering the error between this approximation and the actual change.
How is differentiability defined for a multi-variable function in the video?
-Differentiability for a multi-variable function is defined by considering the change in the function value as the point moves in multiple directions simultaneously and approximating this change using partial derivatives. The function is differentiable if the error terms in these approximations are small and go to zero appropriately.
Why do partial derivatives provide an incomplete picture of differentiability for multi-variable functions?
-Partial derivatives provide an incomplete picture because they only consider changes in one direction at a time, whereas differentiability requires understanding the combined effect of changes in all directions.
What role do error terms play in defining differentiability for multi-variable functions?
-Error terms measure the difference between the actual change in the function value and the approximations given by the partial derivatives. For a function to be differentiable, these error terms must be very small and go to zero as the changes in the variables approach zero.
How is the concept of differentiability used to resolve the issue with the cross function example?
-The cross function example shows that partial derivatives alone are insufficient as the function can have partial derivatives despite being discontinuous. Differentiability, which considers the combined effect of changes in both variables, reveals the discontinuity through the behavior of the error terms.
What powerful theorem is mentioned in the video regarding partial derivatives and differentiability?
-The theorem states that if the partial derivatives of a function exist and are continuous on some open region, then the function is differentiable on that region. This makes partial derivatives useful for proving differentiability, except in pathological cases.

Outlines

00:00

📚 Introduction to Multivariable Differentiability

This paragraph introduces the concept of differentiability for multivariable functions by revisiting single-variable calculus. It discusses the definition of the derivative, the difference quotient, and the geometric interpretation of the derivative as the slope of the tangent line. The paragraph also touches upon the limitations of partial derivatives in capturing the full notion of differentiability and sets the stage for exploring multivariable functions by first understanding single-variable functions.

05:01

🔍 Exploring Differentiability Through Errors and Approximations

This section delves deeper into the concept of differentiability by examining the error term in the context of approximations. It explains how the derivative can be seen as an approximation of the change in the function's value and how the error term, when divided by the change in the independent variable, should approach zero for the function to be differentiable. The paragraph also introduces the idea of using this error-term perspective to define differentiability in multivariable functions.

10:02

📐 Multivariable Differentiability and Partial Derivatives

The paragraph explores the definition of differentiability for multivariable functions, using the concept of partial derivatives and the error-term approach. It explains how partial derivatives can be thought of as the rate of change in one variable while holding others constant. The paragraph also discusses the visual representation of partial derivatives as slopes of secant lines that approach the slope of the tangent line. Furthermore, it introduces the formal definition of differentiability in multivariable functions, emphasizing the conditions that error terms must satisfy for the function to be considered differentiable.

🤔 The Cross Function Example and Differentiability

This paragraph uses the example of the cross function to illustrate the limitations of partial derivatives and the importance of the full differentiability condition. It shows that even though a function may have existing partial derivatives, it may not be differentiable if the error terms do not approach zero as required. The cross function, despite being discontinuous, has existing partial derivatives but fails the differentiability test because the error terms do not vanish. This example highlights the need for a more comprehensive condition than just the existence of partial derivatives.

🌟 The Power of Continuous Partial Derivatives

The final paragraph discusses a powerful theorem related to differentiability, which states that if the partial derivatives of a function are continuous over an open region, then the function is differentiable in that region. This is significant because it provides a more straightforward method to establish differentiability by checking the continuity of partial derivatives. The paragraph emphasizes that this theorem is particularly useful because partial derivatives are generally easier to compute, and their continuity can guarantee differentiability, except in pathological cases.

Mindmap

Keywords

💡Differentiability

Differentiability refers to the property of a function that allows it to be approximated by a linear function, specifically its tangent line, around a given point. In the video, differentiability is explored in both single-variable and multivariable contexts. The theme revolves around defining and understanding when a function can be considered 'nice' or smooth enough to have a derivative, which is a linear approximation of the function's change at a point. The script uses the concept to explain the limitations of partial derivatives and introduces a more comprehensive definition involving error terms.

💡Partial Derivatives

Partial derivatives are a concept in calculus that measures the rate at which a multivariable function changes with respect to one variable, while holding the other variables constant. The video script discusses the limitations of partial derivatives in determining differentiability, using the example of a function that has existing partial derivatives but is not differentiable, thus challenging the intuition that differentiability requires 'nice' behavior at a point.

💡Limit

In the context of the video, a limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. The script uses the limit to define the derivative and differentiability, illustrating how the difference quotient in single-variable calculus and the approximation errors in multivariable calculus approach zero as the change in the input variables approaches zero.

💡Secant Line

A secant line is a straight line that intersects a curve at two distinct points. In the script, the secant line is used to visualize the difference quotient and the concept of the derivative in single-variable calculus. As the points on the curve come closer together, the secant line approaches the tangent line, which represents the instantaneous rate of change of the function at a point.

💡Tangent Line

A tangent line is a linear approximation of a curve at a given point, touching the curve at exactly one point. The video script explains how the tangent line is derived from the limit of secant lines as the points on the curve come infinitely close together. This concept is central to the definition of differentiability and is used to illustrate the smoothness of a function's behavior at a point.

💡Error Term

The error term in the script represents the difference between the actual change in the function's value and the approximation made by the derivative or partial derivative. The video explains how in the definition of differentiability, the error term must approach zero as the change in the input variables approaches zero, ensuring that the approximation is accurate enough to define a derivative.

💡Multivariable Function

A multivariable function is a function that depends on more than one independent variable. The video script delves into the concept of differentiability for such functions, explaining how it extends the ideas from single-variable calculus to higher dimensions. The script uses the example of a surface defined by a function of two variables to illustrate the process of finding partial derivatives and the conditions for differentiability.

💡Continuously Differentiable

Continuously differentiable refers to a function that not only has a derivative but also has a derivative that is continuous. The script mentions a powerful theorem stating that if the partial derivatives of a function are continuous on an open region, then the function is differentiable on that region, highlighting the importance of continuity in the context of differentiability.

💡Cross Function

The cross function is an example used in the script to illustrate a function that is discontinuous but has existing partial derivatives. This example challenges the intuition that functions with existing derivatives should be 'nice' or smooth, and it is used to demonstrate the limitations of partial derivatives in determining differentiability.

💡Approximation

Approximation in the context of the video refers to the process of estimating a value or quantity that is close to, but not exactly, the true value. The script discusses how derivatives and partial derivatives serve as approximations for the change in a function's value, and how the accuracy of these approximations is critical in determining differentiability.

Highlights

Introduction to the concept of differentiability for multivariable functions by revisiting single-variable calculus.

Explaining the definition of the derivative in single-variable calculus and its geometric interpretation.

Visualizing the difference quotient and secant line as a means to understand the slope of a function.

The importance of the limit in defining the tangent line and differentiability.

Rearranging the limit expression to introduce the concept of an error term in the context of differentiability.

The philosophical shift in perspective from limits to error terms in understanding differentiability.

Transitioning to multivariable functions and the analogy with single-variable functions.

The process of defining partial derivatives and their visual representation with secant lines.

The connection between partial derivatives and single-variable derivatives when considering changes in one variable.

Rewriting the partial derivative formula in terms of errors to align with the single-variable case.

The formal definition of differentiability for multivariable functions involving error terms and limits.

The significance of error terms being small and approaching zero for differentiability.

An example illustrating the difference between partial derivatives existing and a function being differentiable.

The case of a discontinuous function with existing partial derivatives, challenging the intuition of differentiability.

The theorem that if partial derivatives are continuous, the function is differentiable on an open region.

The practical application of partial derivatives in proving differentiability and their limitations.

The conclusion that partial derivatives are useful but have limitations, as demonstrated by pathological examples.

Transcripts

Browse More Related Video

Continuity vs Partial Derivatives vs Differentiability | My Favorite Multivariable Function

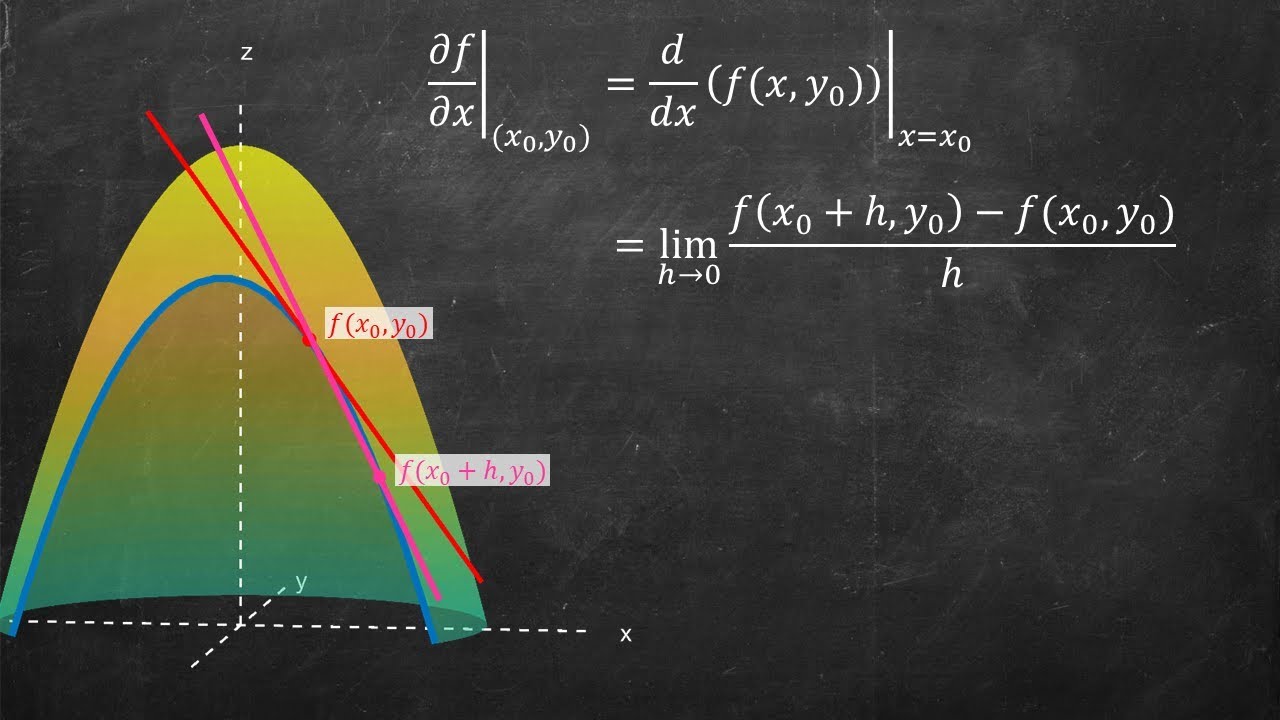
What are derivatives in 3D? Intro to Partial Derivatives

Calculus 3: Tangent Planes and Linear Approximation (Video #14) | Math with Professor V

Calculus 1 Lecture 2.1: Introduction to the Derivative of a Function

Calculus 3 Lecture 13.3: Partial Derivatives (Derivatives of Multivariable Functions)

MultiVariable Calculus - Implicit Differentiation