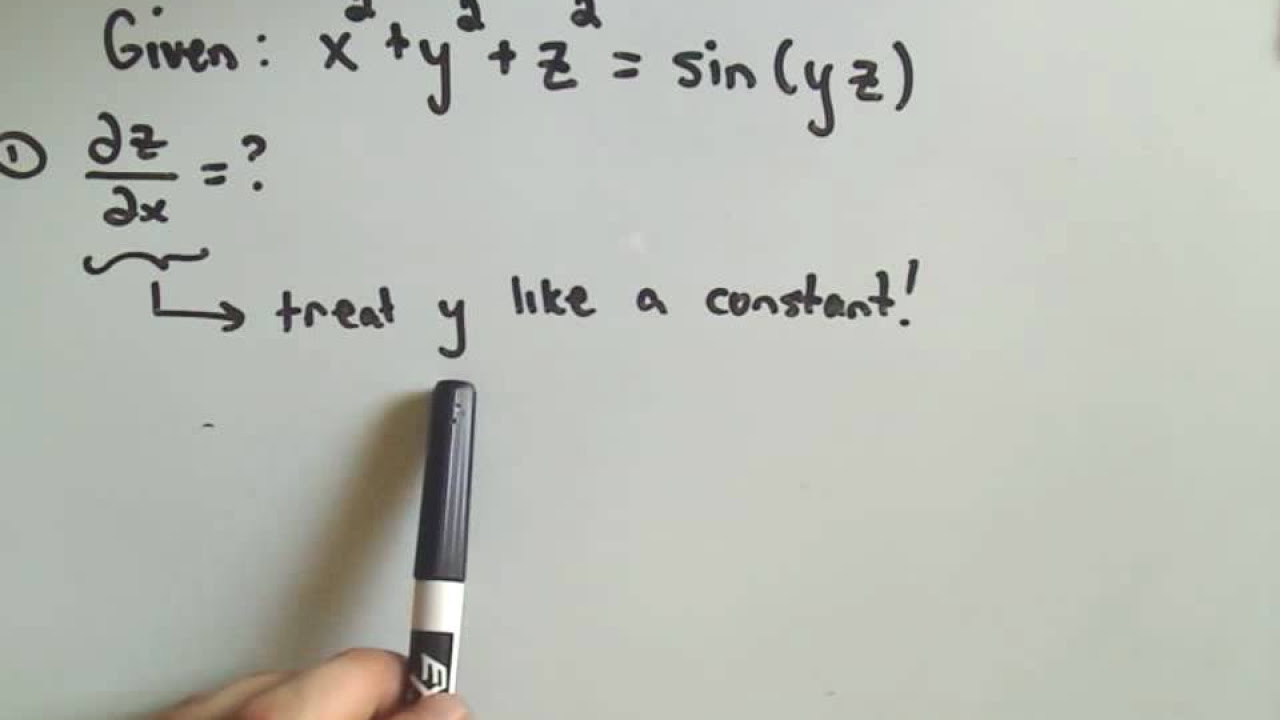Calculus 3 Lecture 13.3: Partial Derivatives (Derivatives of Multivariable Functions)

Professor Leonard

14 Mar 2016148:53

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into the concept of derivatives in multivariable calculus, focusing on partial derivatives and their geometric interpretation as slopes of tangent lines to surfaces. It emphasizes the importance of understanding the meaning behind the calculations and explores the process of finding partial derivatives with respect to different variables. The script also introduces implicit differentiation in multivariable functions and touches on higher-order derivatives, illustrating the concepts with examples and stressing the significance of practice for mastery.

Takeaways

📚 The lesson focuses on understanding the meaning of derivatives in multivariable functions, specifically when there is more than one independent variable.
🔍 In the context of a single variable, the derivative is the slope of the tangent line to a curve at a point, which is unambiguous.
🤔 For multivariable functions, the concept of a derivative is less straightforward due to the potential for an infinite number of tangents at a point on a surface.
📈 To address this, derivatives of multivariable functions are considered along specific directions by holding all but one variable constant, allowing for the calculation of the slope of the tangent line in those directions.
📏 The process involves creating a plane parallel to one of the coordinate planes (e.g., XZ plane for derivatives in the X direction) to restrict the tangent line and simplify the problem.
📝 The notation for partial derivatives is introduced, using a curly 'd' to denote a partial derivative with respect to one of the variables, indicating that other variables are held constant.
👉 The partial derivative with respect to X, denoted ∂f/∂X, involves treating Y as a constant, and vice versa for the partial derivative with respect to Y.
🧩 The concept of implicit differentiation is extended to multivariable functions, where the derivative of an implicitly defined variable (e.g., Z) is found with respect to one of the independent variables (X or Y).
🔄 Mixed partials, or second partial derivatives taken in different orders (e.g., ∂²f/∂X∂Y and ∂²f/∂Y∂X), are shown to be equal for continuously differentiable functions, a property that can be used for checking work or simplifying calculations.
💡 The lesson emphasizes the importance of understanding the geometric interpretation of partial derivatives as slopes of tangent lines to surfaces in specific directions, rather than just memorizing calculation procedures.

Q & A

What is the primary meaning of a derivative when dealing with a single independent variable?
-The primary meaning of a derivative when dealing with a single independent variable is the slope of the tangent line to a curve at a specific point.
What is the ambiguity when trying to define the derivative of a multivariable function in terms of the slope of a surface at a point?
-The ambiguity arises because there are an infinite number of tangents (and thus slopes) to a surface at a given point, making it unclear which one is being referred to without additional context.
How can the concept of a derivative be extended to multivariable functions in a meaningful way?
-The concept of a derivative for multivariable functions can be extended by considering the slope of the tangent line to the surface along a specific direction, which requires holding all but one variable constant.
What does it mean to find the slope of the tangent line to a surface at a point in a certain direction?
-It means finding the derivative of the function along a line that is tangent to the surface at that point and has a specified direction, which is achieved by holding certain variables constant.
What is the purpose of holding a variable constant when finding the derivative of a multivariable function?
-Holding a variable constant simplifies the multivariable function into a single-variable function, allowing us to find the slope of the tangent line along a specific direction on the surface.
What is the term for the derivative of a function with respect to one of its variables while holding other variables constant?
-The term for this is 'partial derivative,' which specifies that the derivative is taken partially with respect to one variable.
How does the notation for partial derivatives differ from the standard derivative notation?
-Partial derivatives are denoted by a curly 'd' or the standard 'd' with a subscript indicating the variable with respect to which the derivative is taken, such as ∂f/∂x or df/dx.
What is the significance of understanding the geometric interpretation of partial derivatives in the context of surfaces?
-Understanding the geometric interpretation helps to visualize the concept of a derivative in higher dimensions, relating it to the slope of a surface along a tangent line in a specific direction, which is crucial for applications in multivariable calculus.
Can you provide an example of how to find the partial derivative of a function like f(x, y) = x^2y + y^3 + 2x with respect to x?
-To find the partial derivative of f(x, y) = x^2y + y^3 + 2x with respect to x, you treat y as a constant and differentiate the function with respect to x, resulting in ∂f/∂x = 2xy + 2.
What is the practical application of understanding partial derivatives in fields like economics or physics?
-In economics, partial derivatives can be used to understand how changes in one variable affect profit or cost while holding other variables constant. In physics, they can describe how a physical quantity changes with respect to one of its variables, such as temperature or pressure, in a controlled environment.

Outlines

00:00

📚 Introduction to Multivariable Derivatives

The script begins by introducing the concept of derivatives for functions with more than one variable. It explains the transition from single-variable derivatives, which represent the slope of a tangent line to a curve at a point, to multivariable derivatives. The instructor emphasizes the importance of understanding the meaning behind derivatives, especially when dealing with multiple independent variables that create a surface in 3D space. The goal is to explore what a derivative of a multivariable function signifies and how it relates to the slope of a surface at a given point.

05:01

🤔 Understanding Multivariable Derivatives

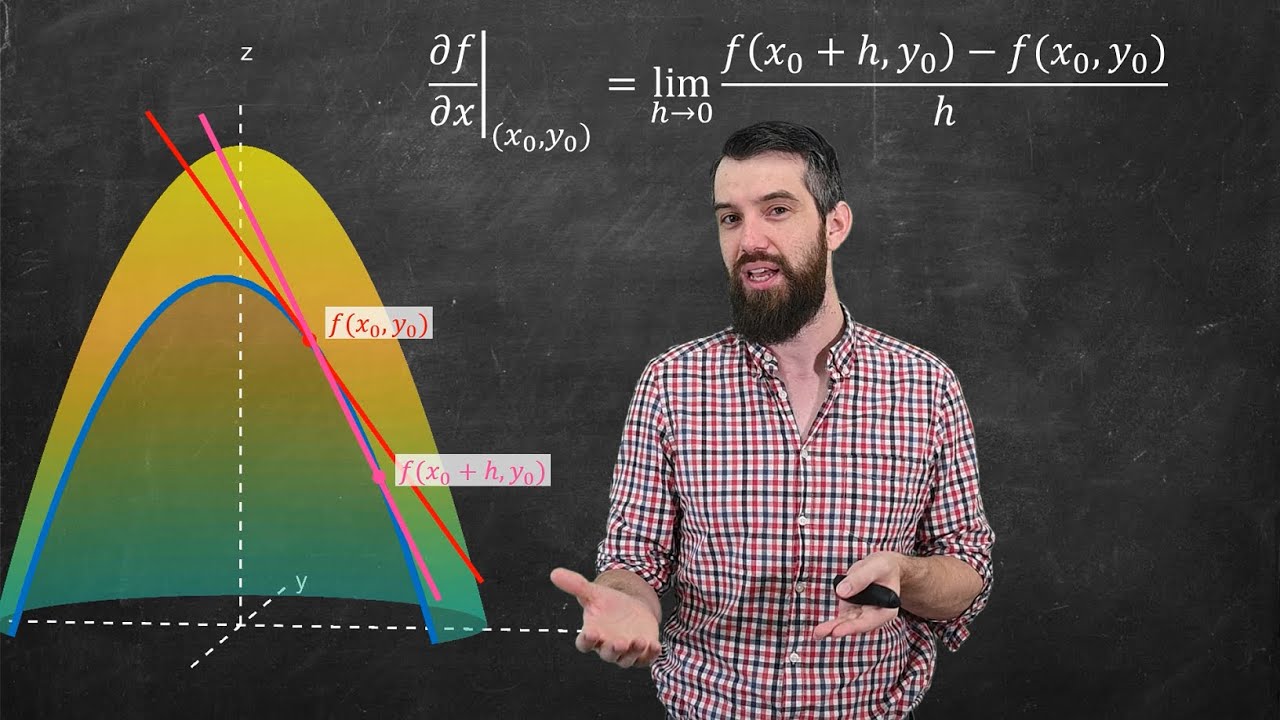
This paragraph delves into the ambiguity of defining a derivative for a multivariable function. The instructor discusses the challenge of determining the slope of a surface at a point, given the infinite number of tangents that can exist at that point. The idea is introduced that to find the slope of a tangent line to a surface, one must specify a direction, leading to the concept of directional derivatives. The instructor also clarifies that the discussion is not about the tangent plane but the line on the surface itself.

10:02

📉 Restricting Direction for Multivariable Derivatives

The instructor explains how to restrict the direction of the derivative to either the X or Y axis to simplify the process of finding the slope of a tangent line to a surface. This involves creating a plane parallel to the XZ or YZ plane, respectively, which intersects the surface at a specific point. By doing so, the multivariable system is temporarily reduced to a single-variable system, allowing for the calculation of the slope of the tangent line along the restricted direction.

15:22

🔍 Focusing on the X Direction for Derivatives

The script focuses on the process of finding the slope of the tangent line to a surface in the X direction. It describes how to create a plane parallel to the XZ plane that intersects the surface at a given point, effectively holding the Y variable constant. This creates a curve on the surface, and the derivative in the X direction can be found by calculating the slope of this curve at the point of intersection, turning the problem into a single-variable derivative scenario.

20:22

📚 Recap and Continuing with the Y Direction

The instructor provides a recap of the concept discussed so far, emphasizing the importance of understanding the process before moving on. The script then continues with the explanation of finding the slope of the tangent line in the Y direction, which involves a similar process of creating a plane parallel to the YZ plane and holding the X variable constant. This results in a curve on the surface, allowing for the calculation of the slope of the tangent line in the Y direction.

25:23

🔑 The Concept of Partial Derivatives

The script introduces the concept of partial derivatives, explaining that they are a specific type of directional derivative. It discusses how partial derivatives are calculated along the X and Y axes by holding one variable constant while finding the derivative with respect to the other. The instructor emphasizes the importance of understanding which variable is being held constant and the direction in which the derivative is being taken.

30:39

📘 Notation and Process of Partial Derivatives

This paragraph discusses the notation used for partial derivatives, explaining the meaning of the curly 'd' symbol and how it indicates a partial derivative with respect to a specific variable. The instructor clarifies the process of taking partial derivatives with respect to X and Y, emphasizing the importance of treating the other variable as a constant. The goal is to find the slope of the tangent line to the surface at a point in either the X or Y direction.

35:40

📌 Practical Examples of Partial Derivatives

The script provides practical examples of calculating partial derivatives, demonstrating the process with specific functions of two variables. It illustrates how to treat one variable as a constant and calculate the derivative with respect to the other variable. The instructor emphasizes the importance of understanding the concept of partial derivatives and knowing when to use the product rule and when not to.

40:46

🤔 Implicit Differentiation for Multivariable Functions

The instructor introduces the concept of implicit differentiation for functions with multiple variables. It explains that when a function is implicitly defined, one variable is considered a function of the others, and differentiation must be performed with respect to a single independent variable. The script discusses the need for product and chain rules when differentiating terms involving the implicitly defined variable.

45:47

📝 Second Partial Derivatives and Higher Order Derivatives

The script discusses the process of finding second partial derivatives and higher order derivatives for functions with multiple variables. It explains that after finding the first partial derivative, one can continue to differentiate with respect to the same variable or switch to a different independent variable. The instructor introduces the concept of mixed partials and emphasizes the importance of understanding the order of differentiation.

50:49

📊 Applications of Partial Derivatives

The instructor provides a real-world example of how partial derivatives can be used to determine how changes in weight or height affect the surface area of a human body. The script demonstrates the practical application of partial derivatives in understanding how different variables impact a specific outcome, such as the stretching of skin due to changes in body size.

55:54

📚 Conclusion and Summary of Key Concepts

In the final paragraph, the instructor summarizes the key concepts covered in the script, including the calculation of partial derivatives, the process of implicit differentiation, and the application of these concepts in real-world scenarios. The script concludes by emphasizing the importance of practice in mastering the calculation of derivatives and understanding their significance in various contexts.

Mindmap

Keywords

💡Derivative

In the context of the video, a derivative is a mathematical concept that represents the rate of change of a function with respect to one of its variables. It is central to the theme of the video, which discusses how to interpret derivatives when dealing with multiple variables. The video script uses the term to explain the slope of a tangent line to a curve at a point, and extends this concept to multivariable functions, where the derivative indicates the rate of change in a specific direction on a surface.

💡Multivariable Function

A multivariable function is a function that depends on more than one independent variable. In the video, the concept is introduced to explain the complexity of finding derivatives in scenarios where there is more than one variable influencing the output. The script gives the example of a function f(x, y) to illustrate how such functions create a surface in three-dimensional space, as opposed to a curve created by a single-variable function.

💡Tangent Line

The tangent line is a concept discussed in the video to describe a line that touches a curve at a single point. The slope of this tangent line is given by the derivative of the function at that point. The script uses the tangent line to transition from the concept of derivatives in single-variable functions to the more complex case of multivariable functions, where the notion of a tangent line becomes less straightforward due to the presence of multiple variables.

💡Slope

Slope is defined as the measure of the steepness of a line, and in the video, it is used to describe the instantaneous rate of change of a function. The script explains that the derivative of a function with one independent variable gives the slope of the tangent line to a curve at a point. This concept is then extended to multivariable functions, where the derivative represents the slope of the tangent to a surface in a specific direction.

💡Partial Derivative

A partial derivative is the derivative of a function with respect to one of its variables, while the other variables are held constant. The video script introduces partial derivatives as a tool to understand the rate of change of a multivariable function in a specific direction. For example, the script discusses taking the partial derivative of a function with respect to x while treating y as a constant, which allows for the analysis of how the function changes along the x-axis.

💡Independent Variable

An independent variable is a variable that can be freely manipulated or changed in an experiment or mathematical model without being dependent on other variables. In the video, the concept is crucial for understanding how derivatives work in multivariable functions. The script explains that when finding a partial derivative, one of the independent variables is treated as the variable of interest, while the others are held constant.

💡Directional Derivative

The directional derivative is a concept mentioned in the script that extends the idea of the partial derivative to any direction in space, not just along the axes. While the video focuses on partial derivatives along the x and y axes, it mentions that directional derivatives allow for the calculation of the rate of change of a function in any specified direction, which is a more general concept.

💡Tangent Plane

A tangent plane is a concept briefly mentioned in the script in contrast to the tangent line. While the video primarily discusses the slope of the tangent line to a curve or surface, it also touches on the idea of a tangent plane, which is a plane that touches a surface at a single point. The script clarifies that it is focusing on the slope of the tangent line, not the tangent plane.

💡Level Curve

A level curve is a curve on a surface where a multivariable function has a constant value. In the video, the script explains that when finding a partial derivative, the process involves restricting the surface to a plane that creates a level curve. This curve represents all points on the surface with the same function value, and the derivative of this curve at a point gives the slope of the tangent line to the surface in the direction of the plane.

💡Chain Rule

The chain rule is a fundamental principle in calculus for finding the derivative of a composite function. Although not the main focus of the video, the script mentions the chain rule in the context of finding derivatives of multivariable functions, especially when dealing with implicit differentiation. The chain rule allows for the derivative of the outer function to be multiplied by the derivative of the inner function.

💡Implicit Differentiation

Implicit differentiation is a technique used when a function is not explicitly given in terms of one variable. The video script touches on this concept towards the end, explaining that it is possible to find partial derivatives of implicitly defined functions by differentiating both sides of the equation with respect to one of the independent variables, while treating the implicitly defined variable as a function of the independent variables.

Highlights

Derivatives with one independent variable are the slope of a tangent line to a curve at a point.

Derivatives with more than one variable are more ambiguous due to the potential for an infinite number of tangents.

A multivariable function creates a surface in 3D space when plotted with two independent variables.

The concept of a derivative for multivariable functions is clarified by considering the slope of a tangent line to a surface at a point in a specific direction.

To find the slope of a tangent line to a surface at a point, restrict the direction to align with one of the axes.

Holding one variable constant turns a multivariable function into a single-variable function, simplifying the derivative process.

Partial derivatives are named for their restriction to part of the possible directions of change in a multivariable function.

The notation for partial derivatives uses a curly 'd' to distinguish them from total derivatives.

Partial derivatives can be thought of as the rate of change of a function with respect to one variable while holding others constant.

The concept of treating a variable as a constant is crucial for understanding partial derivatives.

Product and chain rules are still applicable when finding partial derivatives, but the context of use is different.

Derivatives of constants are zero, which simplifies partial derivatives when variables are held constant.

The slope of a tangent line to a surface in a specific direction is found by taking a partial derivative with respect to that direction.

Higher-order partial derivatives extend the concept of finding slopes to second and further derivatives in restricted directions.

Mixed partials, or second partial derivatives in different orders, are always equal if the function is continuous in a region.

The讲师 demonstrates how to find partial derivatives of complex functions step by step, emphasizing the importance of understanding the process over memorization.

Implicit differentiation is applied to multivariable functions where the dependent variable is not explicitly defined in terms of the independent variables.

The讲师 uses practical examples, such as modeling the surface area of a human body, to illustrate the application of partial derivatives.

Transcripts

Browse More Related Video

Partial Derivatives - Multivariable Calculus

BusCalc 14.2 Partial Derivatives

MultiVariable Calculus - Implicit Differentiation

What is differentiability for multivariable functions??

Partial derivatives - How to solve?

BusCalc 12.4 Implicit Differentiation

Related Tags

Partial Derivatives Calculus Concepts Multivariable Functions Slope of Tangent Rate of Change Surface Area Skin Stretch Business Analytics Engineering Applications Mathematical Differentiation