Tangent Planes (Calculus 3)
TLDRIn this educational video, Houston Matt Prep explains how to find tangent planes to graphs in three-dimensional space, focusing on a circular paraboloid. He illustrates the process by identifying the normal vector from the gradient of the function, demonstrating with examples how to calculate the gradient for different functions, and then using it to derive the equation of the tangent plane at specified points. The video serves as a guide for visualizing and solving for tangent planes in complex mathematical scenarios.
Takeaways
- 📚 The script discusses the concept of tangent planes to graphs in three-dimensional space, specifically focusing on a circular paraboloid.
- 🔍 To find a tangent plane, one needs to identify a point on the graph and determine the normal vector at that point.
- 📐 The normal vector can be found using the gradient of the function, which points in the direction of greatest increase and is perpendicular to the level curves.
- 📈 The gradient is calculated from the partial derivatives of the function with respect to each variable (x, y, and z in 3D space).
- 🧭 For a circular paraboloid, the gradient at a point (x0, y0, z0) is given by the partial derivatives evaluated at that point, resulting in a vector (a, b, c).
- 📉 The script provides an example of finding a tangent plane to the circular paraboloid at the point (-1, -1, 2), using the gradient to determine the normal vector.
- 📝 The general equation of a plane is ax + by + cz = d, where (a, b, c) are the components of the normal vector and d is a constant determined by the point of tangency.
- 🌐 The process involves rearranging the function to express it as a level surface and then taking the gradient to find the normal vector.
- 📊 Another example given is for a function representing an ellipsoid, where the gradient is directly calculated from the function's form as a level surface.
- 📖 The script explains how to plug the point of tangency into the plane's equation to solve for the constant d, completing the equation of the tangent plane.
- 👍 The video aims to help viewers understand how to find tangent planes to curves in three-dimensional space using the gradient and level surfaces.
Q & A
What is the basic equation for a circular paraboloid?
-The basic equation for a circular paraboloid is Z = x^2 + y^2.
How can you determine if a plane is tangent to the bottom point of a paraboloid at the origin?
-If the plane is tangent to the bottom point of the paraboloid at the origin, it is likely to be the XY plane, which can be represented as Z = 0.
What are the two main components required to define a tangent plane to a function at a given point?
-The two main components required to define a tangent plane are a point on the function and a normal vector to the surface at that point.
What is the general equation of a plane in three-dimensional space?
-The general equation of a plane in three-dimensional space is ax + by + cz = D, where a, b, and c are the coefficients of the plane.
How does the gradient vector relate to the tangent plane of a surface?
-The gradient vector is normal to the surface at the point of tangency and thus provides the direction for the normal vector of the tangent plane.
What is the process of finding the normal vector to a surface at a specific point?
-To find the normal vector, you take the gradient of the function representing the surface at the point of interest, which gives the direction of greatest increase and is perpendicular to the level curves on the surface.
How can you find the equation of a tangent plane to a function at a point (x0, y0, z0)?
-You first find the gradient of the function at the point (x0, y0, z0) to get the normal vector. Then, plug the normal vector coefficients and the point into the plane equation ax + by + cz = D, and solve for D to get the complete equation of the tangent plane.
What is the significance of level curves in the context of finding a tangent plane?
-Level curves represent the constant values of the function when viewed from different heights. The gradient vector points in the direction of greatest increase and is perpendicular to these level curves, which helps in visualizing the normal to the surface.
Can you provide an example of finding a tangent plane to the function f(x, y) = √(36 - x^2 - y^2) at the point (2, 4, 4)?
-First, rewrite the function as Z = √(36 - x^2 - y^2), then find the gradient by taking partial derivatives with respect to X, Y, and Z. Evaluate the gradient at the point (2, 4, 4) to get the normal vector. Use this vector in the plane equation and plug in the point to solve for the constant D, resulting in the equation of the tangent plane.
What is the process for finding a tangent plane to an ellipsoid given by the equation x^2/25 + y^2/9 + z^2/b^2 = 1 at a point (x0, y0, z0)?
-Since the ellipsoid is already a level surface, you directly calculate the gradient of the function F(x, y, z) = x^2/25 + y^2/9 + z^2/b^2 - 1. Evaluate the gradient at the point (x0, y0, z0) to get the normal vector, and use it to define the tangent plane equation ax + by + cz = D. Solve for D by substituting the point into the plane equation.
Outlines
📚 Introduction to Tangent Planes on Paraboloids
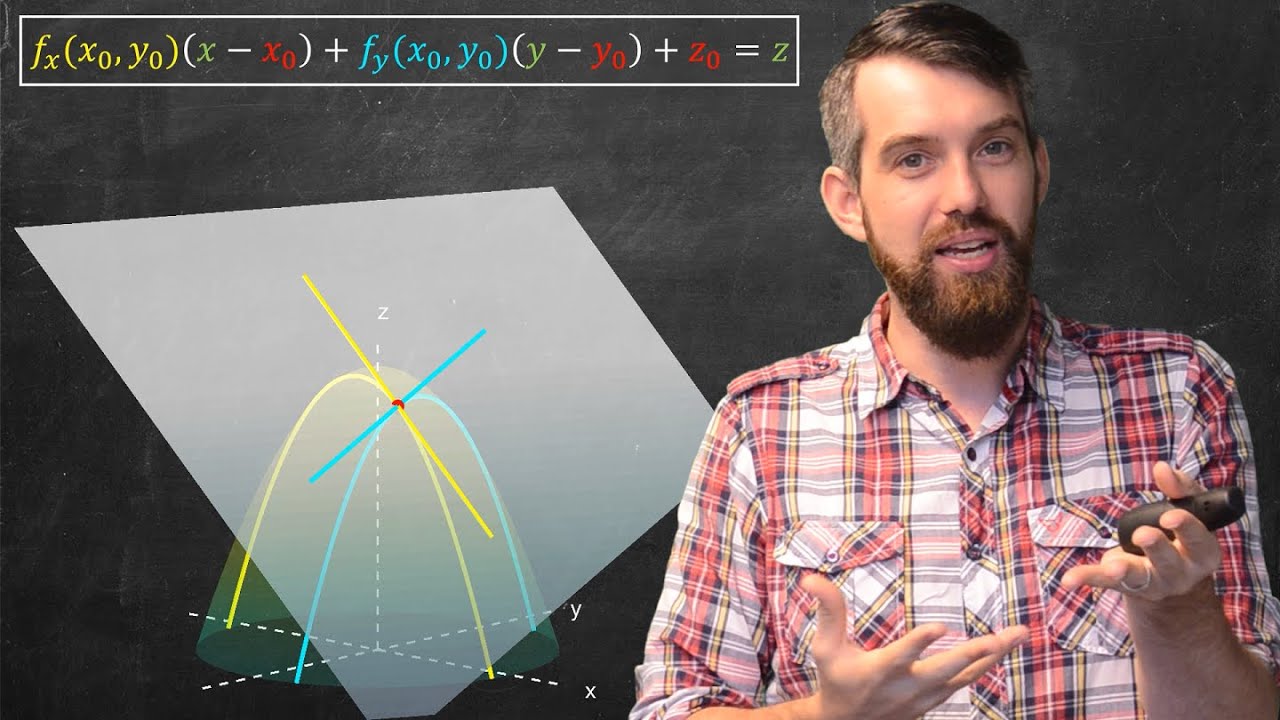
Houston Matt prep introduces the concept of tangent planes in three-dimensional space, specifically focusing on a circular paraboloid. He explains the basic equation for a paraboloid and discusses the process of finding a tangent plane through a given point on the paraboloid, such as the origin. Matt emphasizes that while some tangent planes can be identified by simple observation, a general procedure is needed for arbitrary points. The general equation of a plane is presented, highlighting the need for a point and a normal vector to define a tangent plane. The gradient of the function is introduced as a tool for finding the normal vector, which is perpendicular to the level curves of the function.
🔍 Deriving the Tangent Plane Equation
Matt demonstrates the process of finding the equation of a tangent plane to the circular paraboloid at a point (-1, -1, 2). He rearranges the equation of the paraboloid to express it as a function of three variables and then takes the gradient of this function to find the normal vector. By evaluating the gradient at the specified point, he determines the components of the normal vector. Using this vector and the given point, Matt formulates the equation of the tangent plane and solves for the constant term to complete the equation.
📘 Applying the Process to Different Functions
Matt extends the process to other functions, such as one involving the square root of a constant minus the sum of squared variables. He shows how to rewrite the function as a level surface and calculate its gradient to find the normal vector at a given point (2, 4, 4). The process is repeated for an ellipsoid, where the function is already in the form of a level surface, and the gradient is calculated directly. For each example, Matt evaluates the gradient at the specified point to find the normal vector and then uses it to derive the equation of the tangent plane.
📝 Summarizing the Tangent Plane Finding Process
In the final paragraph, Matt summarizes the steps for finding a tangent plane to a surface defined by a function of x and y. The process involves transforming the function into a form that includes z, calculating the gradient of this three-variable function at the tangent point to obtain the normal vector, and then using this vector to define the plane. He also explains how to solve for the constant in the plane equation by substituting the tangent point. Matt concludes by hoping that the explanation aids viewers in understanding how to find tangent planes in three-dimensional space.
Mindmap
Keywords
💡Tangent Plane
💡Paraboloid
💡Gradient
💡Level Curves
💡Normal Vector
💡Partial Derivatives
💡Ellipsoid
💡Level Surface
💡Equation of a Plane
💡Three-Dimensional Space
Highlights
Introduction to tangent planes in three-dimensional space, specifically for a circular paraboloid.
Basic equation for paraboloids and identifying the XY plane as the tangent at the origin.
General procedure for finding a tangent plane at any point on a function.
Requirement of a point and a normal vector to define a tangent plane.
Understanding the gradient as a tool for finding the direction of greatest increase and its relation to level curves.
Concept of rearranging the equation of a surface to facilitate the calculation of the gradient.
Explanation of how the gradient points in the direction normal to the level curves of a function.
Process of taking the gradient of a function of three variables to find the normal vector to a surface.
Evaluating the gradient at a specific point to determine the normal vector for a tangent plane.
Example of finding the tangent plane to a circular paraboloid at the point (-1, -1, 2).
Demonstration of calculating partial derivatives for the gradient of a function.
Using the gradient to establish the coefficients for the equation of a tangent plane.
Solving for the constant 'D' in the plane equation by substituting the tangent point.
Additional example involving a function with a different form and finding its tangent plane.
Explanation of how to handle surfaces already written as a function of x, y, and z.
Step-by-step guide on changing the form of a surface equation to facilitate gradient calculation.
Final summary of the process for finding a tangent plane to a three-dimensional curve.
Transcripts
Browse More Related Video

Calculus 3: Directional Derivatives and the Gradient Vector (Video #16) | Math with Professor V

Equation of Tangent Calculus Grade 12

Saddle points

Calculus 3: Tangent Planes and Linear Approximation (Video #14) | Math with Professor V
How to find the TANGENT PLANE | Linear approximation of multi-variable functions

Normal Vectors and Equations of Planes (Calculus 3)
5.0 / 5 (0 votes)
Thanks for rating: