Math Antics - Perimeter

mathantics
10 Feb 201407:28
EducationalLearning
32 Likes 10 Comments

TLDRIn this Math Antics lesson, the concept of Perimeter is introduced as the total distance around a geometric shape, measured in linear units like centimeters or miles. The video clarifies that perimeter is a 1-dimensional quantity and demonstrates how to calculate it for various polygons, including triangles, rectangles, and regular hexagons. It emphasizes the importance of units and provides strategies for finding missing side lengths, concluding with the formula for calculating the perimeter of any polygon by summing the lengths of all sides.

Takeaways
  • 📏 Perimeter is the distance around a geometric shape and is measured in units of length.
  • 📐 The units of measurement are crucial when expressing the perimeter to ensure clarity.
  • 🔍 Perimeter specifically refers to the shortest distance around a shape, tracing its border or edge.
  • 🚶 Walking along the edge of a shape gives a practical understanding of what the perimeter represents.
  • 📐 For polygons, the perimeter is calculated by summing the lengths of all sides.
  • 🔢 The formula for the perimeter of a regular polygon is the number of sides multiplied by the length of one side.
  • 📐 For irregular polygons, if some side lengths are unknown, use known lengths and symmetry to deduce the missing lengths.
  • 📐 When calculating the perimeter of a rectangle, add the lengths of all four sides, remembering to include the units.
  • 📐 The process of 'unfolding' a shape into a straight line helps to visualize why perimeter is a 1-dimensional measure.
  • 📚 The script emphasizes the importance of practice in mastering the concept of perimeter and other mathematical skills.
  • 📚 Visit www.mathantics.com for more educational content on mathematics.
Q & A

  • What is the definition of 'Perimeter' in Geometry?

    -Perimeter is the 1-dimensional quantity that represents the distance or length around a geometric shape.

  • Why are units important when discussing perimeter?

    -Units are important because they specify the type of measurement used for the perimeter, such as centimeters, inches, or miles, ensuring clarity and accuracy.

  • What does 'around a shape' mean in the context of perimeter?

    -It refers to the absolute shortest distance possible around a shape, which is the distance you'd get if you traced the path exactly around the border or edge of the shape.

  • How can you visualize the concept of perimeter for a polygon?

    -You can visualize it by imagining walking along the edge of a shape, starting at one vertex and walking along each side until you return to the starting point, measuring the total distance traveled.

  • How is the perimeter of a shape with straight sides, like a polygon, calculated?

    -For polygons, you simply add up the lengths of all the sides to get the total perimeter.

  • What is a regular polygon and how does it simplify the calculation of perimeter?

    -A regular polygon is a polygon where all sides are of equal length. This simplifies the calculation of perimeter by allowing you to multiply the number of sides by the length of one side.

  • How do you find the perimeter of a shape when not all side lengths are given?

    -You use the lengths of the known sides to infer the lengths of the unknown sides, often by using symmetry or other geometric properties, and then sum all side lengths to find the perimeter.

  • Can you provide an example of calculating the perimeter of a triangle from the script?

    -Yes, the example given is a triangle with sides of 3cm, 4cm, and 5cm. The perimeter is calculated as 3 + 4 + 5 = 12 centimeters.

  • What is the perimeter of the rectangle in the script, and how is it calculated?

    -The rectangle has shorter sides of 5m each and longer sides of 10m each. The perimeter is calculated as (5 + 5) + (10 + 10) = 30 meters.

  • How is the perimeter of a 6-sided regular polygon with each side being 4 cm calculated?

    -For a regular polygon, you multiply the number of sides by the length of one side. So, for this polygon, the perimeter is 6 x 4 cm = 24 centimeters.

  • What is the strategy for finding the perimeter of a non-regular polygon with missing side lengths?

    -You use the known side lengths and geometric properties to deduce the missing lengths, then sum all the side lengths to find the perimeter.

Outlines
00:00
📏 Understanding Perimeter in Geometry

This paragraph introduces the concept of perimeter in geometry, explaining it as the 1-dimensional measurement of the distance around a shape. It emphasizes the importance of units in expressing perimeter and clarifies that perimeter represents the shortest distance around a shape, which is the length of the path traced along the shape's border. The explanation includes examples of a 5-sided polygon and a square to illustrate how perimeter is calculated for different shapes, highlighting that it is a linear measure even when applied to two-dimensional shapes. The paragraph also discusses the process of calculating the perimeter of polygons, especially focusing on how to find the perimeter of a triangle and a rectangle by adding the lengths of their sides.

05:00
🔍 Calculating Perimeter for Regular and Irregular Polygons

This paragraph continues the discussion on perimeter by explaining how to calculate it for regular polygons, where all sides are of equal length, using a simple multiplication formula. It then presents a more complex scenario involving an irregular hexagon with missing side lengths, demonstrating a method to deduce the unknown lengths by using the known vertical and horizontal side lengths. The process involves visualizing the rearrangement of known sides to estimate the unknown ones, ultimately allowing for the calculation of the total perimeter by summing all side lengths. The paragraph concludes with a reminder of the importance of units and the necessity of practice in mastering mathematical concepts, inviting viewers to learn more at the provided website.

Mindmap
Keywords
💡Perimeter
Perimeter is the main concept of the video, defined as the distance or length around a geometric shape. It is a one-dimensional quantity measured in units of length such as centimeters or miles. The video emphasizes the importance of units when discussing perimeter. The script illustrates the concept by explaining that the perimeter is the shortest distance around a shape, which is found by tracing the path along the border of the shape. For example, a 5-sided polygon with each side measuring 10 meters would have a perimeter of 50 meters.
💡1-dimensional quantity
A 1-dimensional quantity refers to something that extends in only one direction, having length but no width or height. In the context of the video, the perimeter is a 1-dimensional quantity because it represents the length of the boundary of a two-dimensional shape. The script clarifies this by explaining that even though perimeter applies to 2D shapes, it is the measurement of the lines that enclose the shape, hence it is 1D.
💡Units of length
Units of length are standard measures used to express the length or distance of an object. The script highlights the significance of units when calculating the perimeter, as they provide context to the measurement. Examples given include centimeters, inches, and miles, which are used to specify the perimeter of shapes such as a triangle with sides of 3cm, 4cm, and 5cm, resulting in a perimeter of 12 centimeters.
💡Polygon
A polygon is a two-dimensional shape with a finite number of straight sides. The video focuses on calculating the perimeter of polygons, which is straightforward because they consist of straight sides. The script provides examples of different polygons, including a triangle, rectangle, and a hexagon, and demonstrates how to find their perimeters by adding the lengths of their sides.
💡Regular polygon
A regular polygon is a polygon where all sides and angles are equal. The script explains that calculating the perimeter of a regular polygon is simplified because all sides are of the same length. It uses the example of a 6-sided regular polygon with each side being 4 cm, and shows that the perimeter can be found by multiplying the number of sides (6) by the length of one side (4 cm), resulting in 24 centimeters.
💡Irregular polygon
An irregular polygon is a polygon where the sides are of different lengths. The video script presents a scenario with an irregular hexagon where not all side lengths are given, and it teaches viewers how to deduce the missing lengths using the known sides, ultimately calculating the perimeter by summing all sides.
💡Triangle
A triangle is a polygon with three sides and three angles. The script uses a triangle with sides of 3 cm, 4 cm, and 5 cm to demonstrate how to calculate the perimeter of a polygon by adding the lengths of its sides, resulting in a perimeter of 12 centimeters.
💡Rectangle
A rectangle is a four-sided polygon with opposite sides equal in length and all angles being right angles. The video script illustrates the calculation of a rectangle's perimeter by adding the lengths of its sides, showing a rectangle with shorter sides of 5 meters and longer sides of 10 meters, resulting in a perimeter of 30 meters.
💡Multiplication
Multiplication is a mathematical operation used to calculate the total of adding a number to itself repeatedly. In the context of the video, multiplication is presented as a shortcut for calculating the perimeter of a regular polygon by multiplying the number of sides by the length of one side, as shown with the 6-sided regular polygon example.
💡Practice
Practice is the act of repeatedly performing an activity or exercise to improve or master a skill. The video script concludes with an encouragement to practice, emphasizing that becoming proficient in math requires consistent and deliberate effort, which is a universal principle applicable to learning any skill.
Highlights

Perimeter is defined as the distance or length around a geometric shape.

Perimeter is a 1-dimensional quantity measured in units of length like centimeters or miles.

The importance of units when discussing perimeter is emphasized.

The concept of 'around a shape' refers to the shortest possible distance tracing the shape's border.

A practical example of perimeter is walking along the edge of a 5-sided polygon.

If each side of the polygon is 10 meters, the perimeter is calculated by summing the side lengths to 50 meters.

Perimeter can be visualized by unfolding a shape like a square into a straight line.

The formula for calculating the perimeter of polygons with straight sides is by adding the lengths of all sides.

For polygons with curves, like circles, the calculation of perimeter is more complex and will be discussed in another video.

A triangle's perimeter is found by adding the lengths of its three sides, with units included.

A rectangle's perimeter is calculated by adding the lengths of its two pairs of equal sides, remembering to include units.

Regular polygons, where all sides are equal, have a perimeter calculated by multiplying the number of sides by the side length.

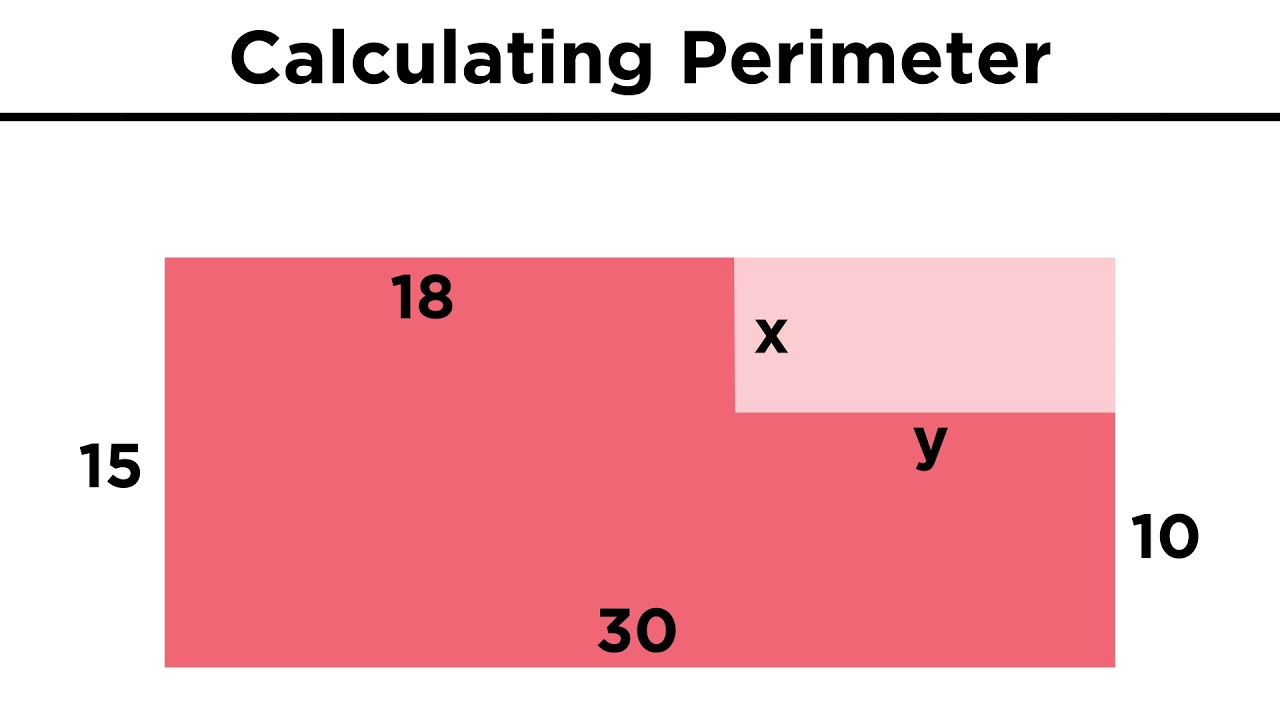
For irregular polygons, if some side lengths are missing, use known side lengths to deduce the unknowns.

An example of deducing missing side lengths by combining known vertical and horizontal side lengths.

Once all side lengths are known, sum them to find the perimeter of an irregular polygon.

The final example calculates the perimeter of a 6-sided irregular polygon with a total of 50 inches.

The lesson concludes with the reminder that perimeter is the total distance around any polygon, and practice is key to mastering math.

Transcripts

Browse More Related Video

Calculating the Perimeter of Polygons

How to Calculate Pi, Archimedes' Method

Math Antics - Polygons

Area and Perimeter of Irregular Shapes - Tons of Examples!

Math Antics - Area

Area of an Oblique Triangle - SAS & SSS - Heron's Formula, Trigonometry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
GeometryPerimeterDistanceUnitsPolygonsCalculationShapesEducationMathematicsTutorial