Area and Perimeter of Irregular Shapes - Tons of Examples!
TLDRIn this video, we explore finding the area and perimeter of irregular shapes. Starting with an example, we break down a complex shape into simpler components, calculate the perimeter by summing up all sides, and find the area by dividing the shape into rectangles and triangles. We then tackle additional examples, including a shape combining a rectangle and a semicircle, demonstrating the use of formulas for rectangles, triangles, and circles. The video emphasizes key formulas, such as length times width for rectangles and πr² for circles, ensuring a comprehensive understanding of the topic.
Takeaways
- 📏 Finding the area and perimeter of irregular shapes involves breaking them down into simpler components.
- 🔢 The perimeter is calculated by adding the lengths of all sides.
- 📐 For rectangles, the area is found by multiplying length and width.
- 🧮 For semicircles, the area is half of πr² and the circumference is πr.
- ✂️ Irregular shapes can be divided into rectangles, triangles, and semicircles to simplify calculations.
- 📏 The perimeter of a shape is the total distance around it, including all sides and any curved sections.
- 🔲 For triangles, the area is half of the base times the height.
- 📏 Pythagorean theorem is used to find the hypotenuse in right triangles.
- 📐 Basic formulas include: area of a rectangle (length x width), area of a triangle (1/2 base x height), area of a circle (πr²), and circumference of a circle (2πr).
- 📝 Ensure you know these formulas for tests or practical applications involving geometric shapes.
Q & A
What is the main focus of the video?
-The video focuses on finding the area and perimeter of irregular shapes and figures.
How is the perimeter of an irregular shape calculated in the video's first example?
-The perimeter is calculated by adding the lengths of all sides of the shape, which includes the sides of 5, 6, 7, 12, and 5 units, totaling 46 units.
What is the formula used to find the area of a rectangle in the video?
-The area of a rectangle is found by multiplying its length by its width.
How does the video calculate the area of a semicircle attached to a rectangle?
-The area of the semicircle is calculated using the formula (1/2) * π * r^2, where r is the radius of the semicircle.
What is the perimeter of the figure with a rectangle and a semicircle attached, as calculated in the video?
-The perimeter is 25.4 units, which includes the lengths of the rectangle sides, the diameter of the semicircle, and the circumference of the semicircle.
How is the area of a triangle in the video's third example calculated?
-The area of the triangle is calculated using the formula (1/2) * base * height, which in this case is (1/2) * 8 * 4, resulting in 16 square units.
What is the total area of the figure consisting of a rectangle and a triangle, as shown in the third example of the video?
-The total area is 48 square units, which is the sum of the areas of the rectangle (32 square units) and the triangle (16 square units).
How is the perimeter of the figure with a rectangle and a triangle calculated in the video?
-The perimeter is calculated by adding the lengths of all sides of the rectangle and the triangle, which totals 27 units.
What is the formula used to find the area of a triangle in the fourth example of the video?
-The area of the triangle is found using the formula (1/2) * base * height, which in this case is (1/2) * 9 * 8, resulting in 36 square units.
How does the video calculate the area of a semicircle with a diameter of 5 units?
-The area of the semicircle is calculated using the formula (1/2) * π * (d/2)^2, which results in approximately 9.8 square units when using π ≈ 3.14.
What is the total perimeter of the figure with a semicircle on top and a triangle on the bottom, as calculated in the video?
-The total perimeter is approximately 69.89 units, which includes the lengths of the sides of the rectangles, the hypotenuse of the triangle, and the circumference of the semicircle.
Outlines
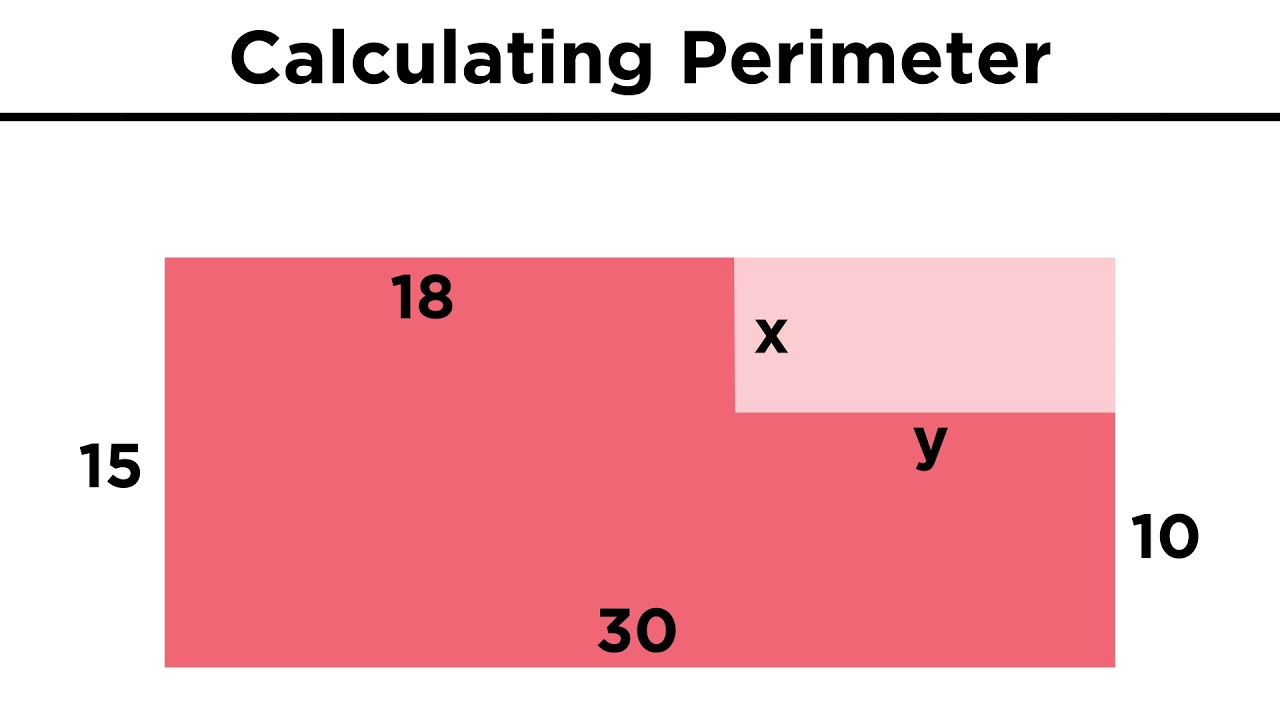
📏 Calculating Perimeter and Area of Irregular Shapes
This paragraph introduces the topic of calculating the perimeter and area of irregular shapes. It begins with an example of an irregular shape with sides of 5, 6, and 12 inches. The process of finding the perimeter by adding the lengths of all sides is explained, resulting in a total of 46 units. The area calculation is demonstrated by dividing the shape into two rectangles, calculating the area of each, and summing them up to get a total area of 90 square units. The paragraph also briefly introduces a second example involving a rectangle and a semi-circle, prompting the viewer to calculate the area and perimeter.
📐 Area and Perimeter of Shapes with a Semi-circle
In this paragraph, the focus shifts to calculating the area and perimeter of a figure consisting of a rectangle attached to a semi-circle with dimensions of 5 by 6 inches. The area calculation includes the rectangle's area (30 square inches) and the semi-circle's area, which is derived from the formula for the area of a circle, πr², and then halved to get 14.1 square inches. The total area is thus 44.1 square inches. For the perimeter, the paragraph explains how to calculate the semi-circle's circumference (9.42 units) and adds it to the rectangle's sides, resulting in a total perimeter of 25.4 units.
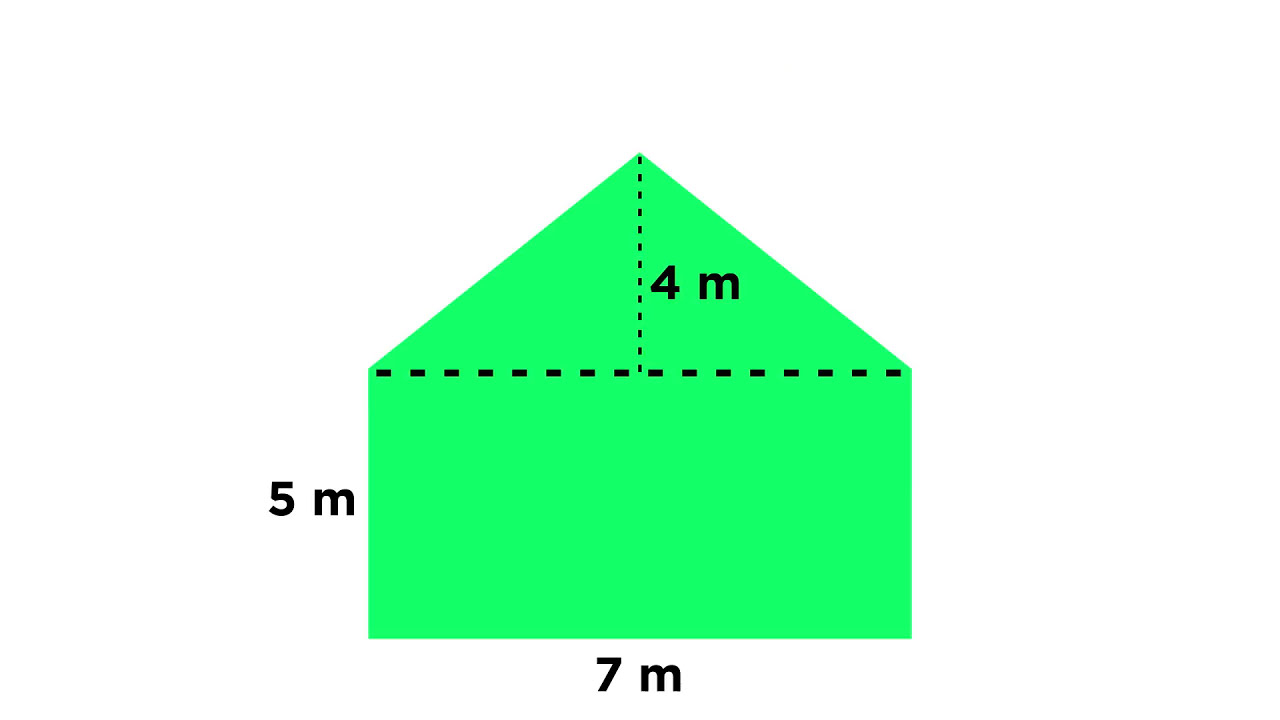
🔍 Mixed Shape Calculations: Rectangle, Triangle, and Semi-circle
The paragraph presents a complex figure composed of a rectangle, a triangle, and a semi-circle with various dimensions. It guides through the process of calculating the area of each component: a rectangle (96 square units), another rectangle (35 square units), and a triangle (36 square units). The semi-circle's area is calculated using the formula for a circle's area and then halving it, resulting in approximately 9.8 square units. The total area is summed up to 176.8 square units. The perimeter calculation involves finding the semi-circle's circumference and the hypotenuse of the right triangle using the Pythagorean theorem, culminating in a total perimeter of approximately 69.89 units.
📘 Recap of Formulas for Area and Perimeter Calculations
The final paragraph serves as a recap of the formulas used throughout the video for calculating the area and perimeter of various shapes, including rectangles, triangles, and circles (or semi-circles). It emphasizes the importance of knowing these formulas for tests and provides a brief overview of each: the area of a rectangle (length times width), the perimeter (sum of all sides, 2l + 2w), the area of a triangle (1/2 base times height), the use of the Pythagorean theorem for right triangles, and the formulas for the area and circumference of a circle (πr² and 2πr, respectively). It also mentions the simplified use of π as 3.14 for these calculations.
Mindmap
Keywords
💡Area
💡Perimeter
💡Irregular Shapes
💡Rectangle
💡Semi-circle
💡Triangle
💡Pythagorean Theorem
💡Circumference
💡Diameter
💡pi (π)
Highlights
The video focuses on calculating the area and perimeter of irregular shapes and figures.
An example is given to demonstrate the process of finding the perimeter by adding the lengths of all sides.
The area of an irregular shape is calculated by breaking it down into rectangles and finding the sum of their areas.
A rectangle attached to a semi-circle is used as an example to explain area calculation, including the formula for the area of a semi-circle.
The perimeter of a figure with a rectangle and a semi-circle is calculated by adding the lengths of straight sides and the circumference of the semi-circle.
A triangle attached to a rectangle is used to illustrate the calculation of both area and perimeter, incorporating the Pythagorean theorem for missing sides.
The area of a rectangle is found using length times width, and for a triangle, it's half the product of base and height.
An example with a semi-circle on top and a triangle on the bottom demonstrates the step-by-step process of calculating area and perimeter.
The importance of identifying the dimensions of each shape within an irregular figure to calculate area and perimeter is emphasized.
The formula for the area of a semi-circle is one half pi times the radius squared, and the circumference is pi times the radius.
The Pythagorean theorem is applied to find the hypotenuse of a right triangle within an irregular figure for perimeter calculation.
A summary of formulas for area and perimeter of rectangles, triangles, and circles is provided for reference.
The video concludes with a recap of the formulas and a reminder to apply them for solving problems related to irregular figures.
The video provides a practical approach to solving geometry problems involving irregular shapes by breaking them down into simpler shapes.
The use of the Pythagorean theorem for right triangles within complex figures is highlighted as a key method for finding missing lengths.
The importance of rounding pi to 3.14 for simplicity in calculations is mentioned, with a note that more precision can be achieved with additional decimal places.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: