GeoGebra - Create Interactive Unit Circle with Sine Curve

Study Force
6 Oct 202107:22
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video teaches viewers how to create an interactive unit circle and sine curve in GeoGebra. Starting with a unit circle, the tutorial progresses to generating a dynamic sine curve that updates as the terminal arm moves. The process includes creating points, angles, and line segments, and adjusting the x-axis to reflect radians. The video also guides on adding a dashed vertical line from the sine curve to the x-axis, completing the interactive visualization, which is ideal for introductory trigonometry classes.

Takeaways
  • πŸ“š The lesson is about creating an interactive unit circle and sine curve using GeoGebra.
  • πŸ“ˆ The demonstration shows a completed interactive unit circle and sine curve in GeoGebra.
  • πŸ“ The process starts with creating a new GeoGebra file and placing points for the center and the radius.
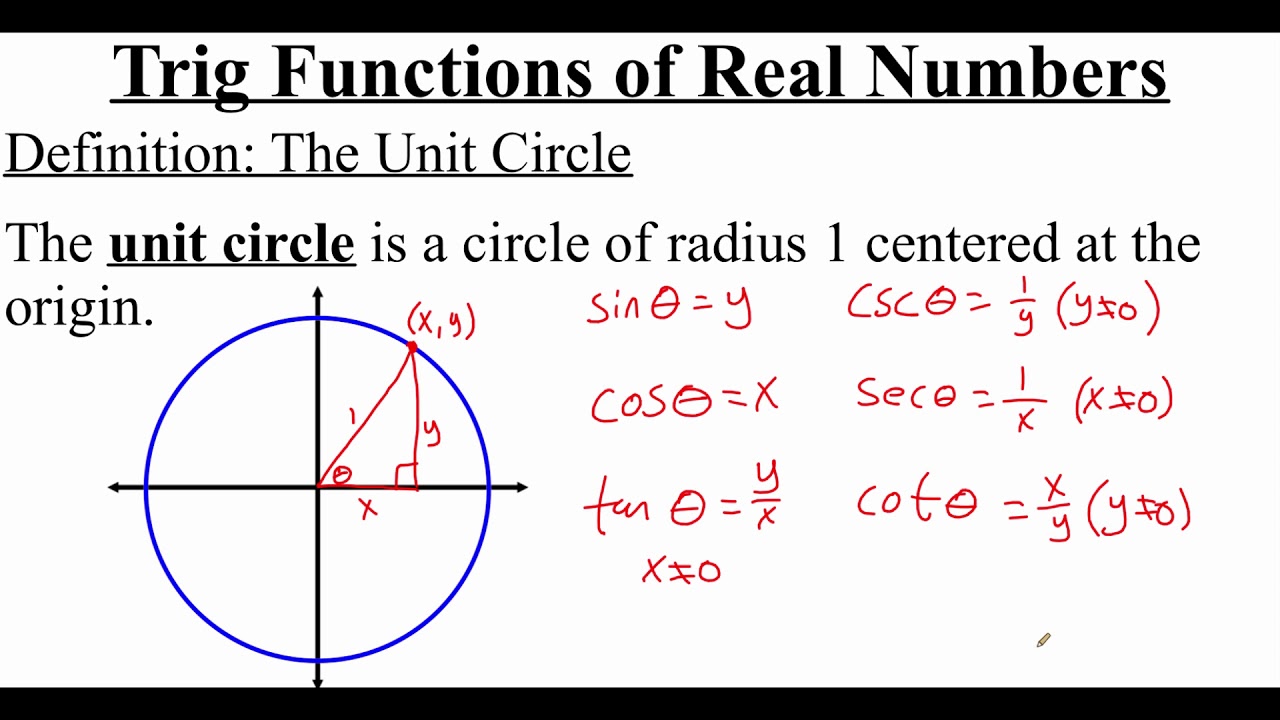
  • πŸ”Ά The unit circle is drawn with a radius of 1, connecting the center point to the point at (1, 0).
  • πŸ“ A terminal arm is created using the 'angle' function and connecting points C, A, and B.
  • πŸ“ A line segment is drawn from point A to point C to represent the terminal arm's projection.
  • πŸ“‰ A dashed vertical line is added from point C to the x-axis to represent the sine value.
  • πŸŒ€ The x-axis is adjusted to reflect values in radians by setting the distance in pi over two.
  • πŸ“Š A sine function is created with 'f(x) = sine(x)' and limited between 0 and the angle alpha.
  • πŸ”‘ Dynamic point D is placed along the sine curve with coordinates based on the angle alpha.
  • πŸ“Œ A vertical line segment from point E to the x-axis is created to represent the sine value visually.
Q & A

  • What is the main purpose of the lesson described in the transcript?

    -The lesson aims to demonstrate how to create an interactive unit circle and its relation to the sine curve using GeoGebra software.

  • Why is the unit circle created with a radius of 1?

    -The unit circle is created with a radius of 1 to standardize the trigonometric ratios and simplify the demonstration of trigonometric functions.

  • How does the script suggest creating the terminal arm of the unit circle?

    -The script suggests using the 'angle' function in GeoGebra to connect points C to A and then to B, or alternatively B, A, C to create the terminal arm.

  • What is the significance of the dashed vertical line from point C to the x-axis?

    -The dashed vertical line represents the perpendicular drop from point C to the x-axis, which is used to illustrate the sine value at different angles.

  • How can the x-axis be adjusted to reflect values in radians?

    -The x-axis can be adjusted to reflect values in radians by going to 'Advanced Preferences' and setting the x-axis distance in terms of pi over two.

  • What function is used to create the sine curve in GeoGebra?

    -The sine function is used, represented as 'f of x is equal to sine x', with the range limited between 0 and 2 pi or controlled by the angle alpha.

  • How is the point D created along the sine curve?

    -Point D is created using the 'dynamic coordinates' function, with its x-coordinates based on the angle alpha and y-coordinates matching those of point C.

  • What is the purpose of the vertical line segment from point E to the x-axis?

    -The vertical line segment from point E to the x-axis is used to visually represent the sine value at the current position of the terminal arm.

  • How can the appearance of the vertical line segment be modified in GeoGebra?

    -The appearance of the vertical line segment can be modified by changing its style to dashed and its color to red, and by removing the label for clarity.

  • What is the final outcome of following the script's instructions?

    -The final outcome is an interactive and dynamic sine curve that updates based on the position of the terminal arm on the unit circle.

  • How can viewers get help if they have questions about the lesson?

    -Viewers can leave questions in the comment section below the video or visit the website mentioned in the video's description for further assistance.

Outlines
00:00
πŸ“š Creating an Interactive Unit Circle for Trigonometry

This paragraph introduces a tutorial on creating an interactive unit circle related to the sine curve in GeoGebra. The process starts by setting up a new GeoGebra file, placing points at the center and on the coordinate axes to define a unit circle with a radius of 1. The tutorial then guides through creating a terminal arm using the angle function and extending a line segment from point A to point C. It also explains how to add a dashed vertical line from point C to the x-axis, modifying its properties for clarity. The aim is to demonstrate the relationship between the terminal arm's angles and the sine curve, with dynamic adjustments to the x-axis to reflect radians and the creation of a sine function that adjusts based on the angle alpha.

05:02
πŸ“ˆ Dynamic Sine Curve Generation Based on Unit Circle

The second paragraph continues the GeoGebra tutorial by focusing on generating a dynamic sine curve. It begins with placing a point D along the sine curve using dynamic coordinates based on angle alpha, with its y-coordinate matching that of point C. The paragraph explains how to create a vertical line segment from point E to the x-axis, similar to the one created earlier but now associated with the sine curve. The tutorial concludes by showing the dynamic generation of the sine curve as point C is moved, with the option to remove unnecessary labels for a cleaner visualization. The paragraph ends with an invitation for viewers to ask questions or visit the website for further information.

Mindmap
Keywords
πŸ’‘Interactive Unit Circle
An interactive unit circle is a graphical tool used in mathematics, particularly in trigonometry, to visualize and understand the relationships between angles and their corresponding trigonometric functions. In the context of the video, the interactive unit circle is created using GeoGebra software to dynamically illustrate the sine curve as the terminal arm of an angle moves around the circle. The unit circle has a radius of 1, and its interaction is central to the video's demonstration of trigonometric concepts.
πŸ’‘Sine Curve
The sine curve is a fundamental element in trigonometry, representing the y-values of the sine function over a range of angles. In the video, the sine curve is generated in relation to the unit circle, showing how the sine of an angle is equal to the y-coordinate of a point on the circle where the terminal arm intersects. The sine curve is dynamically created as the angle changes, providing a visual understanding of how the sine function works.
πŸ’‘GeoGebra
GeoGebra is a dynamic mathematics software that allows users to create interactive graphics and simulations. In the video, GeoGebra is used to construct the interactive unit circle and sine curve, making it an essential tool for demonstrating the trigonometric concepts. The script describes how to use GeoGebra's functions and tools to create the visual elements that teach the relationship between the unit circle and the sine curve.
πŸ’‘Terminal Arm
The terminal arm is a line segment in a circle that starts at a fixed point (usually the center of the circle) and extends to a point on the circumference, representing an angle. In the video, the terminal arm is used to explore the sine function by moving a point along the unit circle, thereby changing the angle and dynamically updating the sine curve.
πŸ’‘Radians
Radians are a unit of angular measure used in trigonometry, where an angle of 1 radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. The video script mentions changing the x-axis to reflect values in radians, which is important for accurately representing the sine function's behavior over the unit circle.
πŸ’‘Angle
An angle is a measure of rotation from a starting point. In the context of the video, angles are used to define positions on the unit circle and to calculate the sine values. The script describes creating an angle using the 'angle' function in GeoGebra, which is essential for constructing the terminal arm and exploring the sine curve.
πŸ’‘Line Segment
A line segment is a part of a line that is bounded by two distinct end points. In the video, line segments are created to represent various components of the unit circle and sine curve, such as the terminal arm and the vertical lines from points on the sine curve to the x-axis. The script provides specific instructions on how to create and style these line segments using GeoGebra.
πŸ’‘Dynamic Coordinates
Dynamic coordinates refer to the ability to define points in a way that their positions change in response to other elements in the model. In the video, the point on the sine curve, labeled 'd', is given dynamic coordinates that change with the angle 'alpha', allowing it to move along the sine curve as the terminal arm rotates.
πŸ’‘Dashed Line
A dashed line is a type of line style characterized by a series of dashes rather than a solid line. In the video, dashed lines are used to represent certain elements, such as the vertical line from point 'c' to the x-axis and the line from point 'e' to the x-axis, providing a visual distinction and clarity to the interactive unit circle and sine curve.
πŸ’‘Function
In the context of the video, a function refers to a mathematical rule that assigns to each element from a set of inputs (domain) exactly one element from a set of possible outputs (codomain). Specifically, the sine function is used to create the sine curve, with the script detailing how to define and apply the sine function in GeoGebra to generate the curve dynamically.
πŸ’‘Preferences
Preferences in GeoGebra allow users to customize the appearance and behavior of the software to suit their needs. The video script mentions adjusting the 'advanced preferences' for the x-axis to display values in radians, which is a preference setting that helps in accurately representing the trigonometric functions on the unit circle.
Highlights

Introduction to creating an interactive unit circle related to the sine curve on GeoGebra.

Demonstration of the app's potential appearance after completion.

Explanation of how the app can be used in an introductory trigonometry class.

Starting a new GeoGebra file and placing a point at the center.

Creating a second point to define the unit circle with a radius of 1.

Connecting points to create a circle and zooming in for clarity.

Using the angle function to create a terminal arm and adjusting the angle direction.

Creating a line segment from point A to point C to represent the terminal arm.

Moving point C to observe angles ranging from 0 to 360 degrees.

Incorporating a dashed vertical line from point C to the x-axis.

Using the segment tool with given length to create a line segment to the x-axis.

Modifying the line segment to be dashed and red for better visualization.

Changing the x-axis to reflect values in radians for the sine curve.

Creating a function for sine with a dynamic range based on the angle alpha.

Recreating the terminal arm after it disappeared during modifications.

Dynamically generating the sine curve based on the angle created by moving point C.

Creating a point along the sine curve with dynamic coordinates based on angle alpha.

Styling the vertical line segment from the sine curve point to the x-axis as dashed and red.

Finalizing the dynamic sine curve generation and offering customization tips.

Invitation for questions and reference to the website for further information.

Transcripts

Browse More Related Video

Unit Circle Definition of Trig Functions

How to Remember the Unit Circle (NancyPi)

Vector components from magnitude and direction

The Unit Circle, Basic Introduction, Trigonometry

4.3.4 Trigonometric Functions of Real Numbers

Trigonometry: Unit Circle

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryGeoGebraUnit CircleSine CurveInteractiveEducationalMathematicsTeaching ToolDynamic GraphsClassroom App