Tukey Method - One-Way ANOVA

Pat Obi
25 Jan 201807:37
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial introduces the Tukey method for post-ANOVA pairwise comparison of population means. It explains the process of rejecting the null hypothesis of equal means in a one-factor ANOVA, followed by using the Tukey method to identify significant differences between group means. The video demonstrates calculating the critical Q value using the studentized range distribution and comparing it to absolute mean differences. It concludes with an interesting point about statistical evidence differing from mathematical reasoning.

Takeaways
  • 📚 The video introduces the Tukey method for pairwise comparison of population means in a one-factor ANOVA.
  • 🔍 The Tukey method is a post-ANOVA test used when the null hypothesis of equal population means is rejected.
  • ❌ The null hypothesis states that there are no regional differences among the three population means.
  • 📉 If the null hypothesis is not rejected, no further analysis is needed.
  • 🔑 If the null hypothesis is rejected, further analysis is required to identify which means differ from the others.
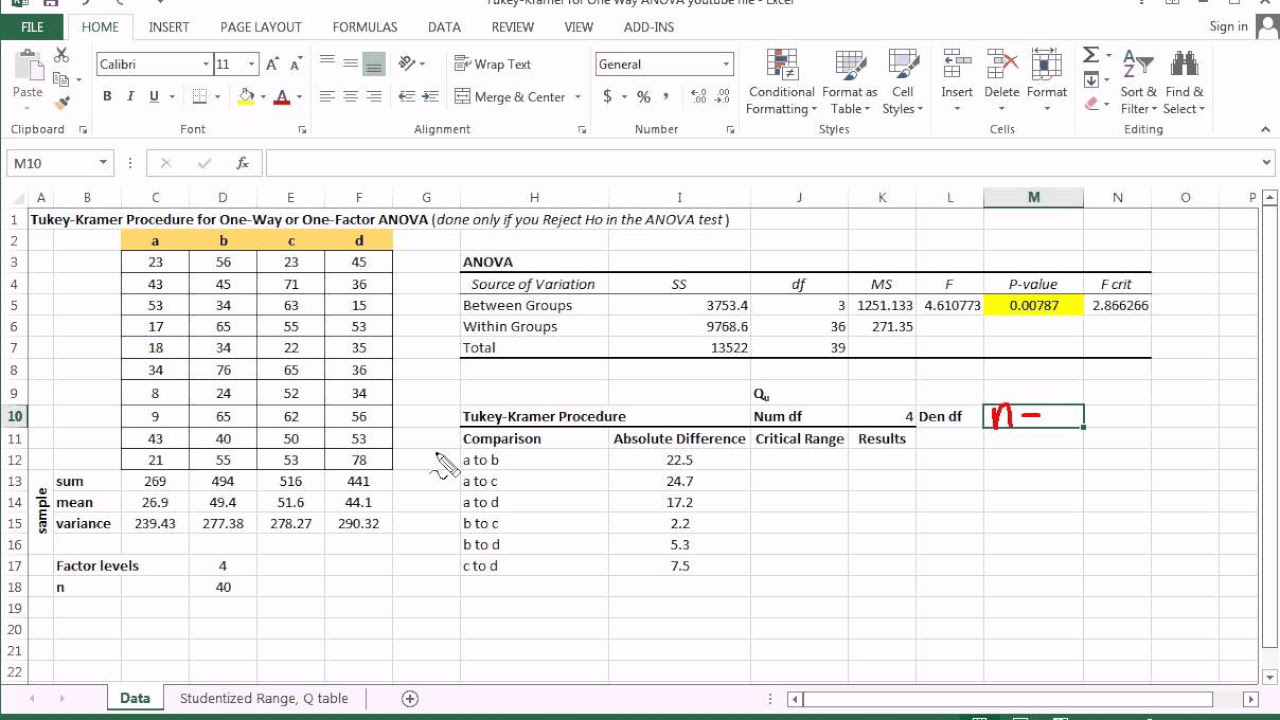
  • 📊 The video uses a dataset to demonstrate the ANOVA process and shows that the p-value is less than 0.05, leading to the rejection of the null hypothesis.
  • 📈 The Tukey method involves comparing the absolute differences between sample means to a critical value derived from the studentized range distribution.
  • 🔢 The critical value (Q statistic) is calculated using the mean square error, the sample size of the smallest group, and a factor from the studentized range distribution.
  • 📝 The degrees of freedom for the Q statistic are determined by the number of treatments and the total sample size.
  • 🔎 The video provides a step-by-step guide on how to calculate the Q statistic and compare it with the absolute mean differences.
  • 🚫 The results show statistical evidence of a significant difference between the means of populations 1 & 2, but not between 1 & 3 or 2 & 3, highlighting the difference between statistical analysis and mathematical reasoning.
Q & A

  • What is the purpose of the Tukey method in the context of ANOVA?

    -The Tukey method is used for post-ANOVA analysis to identify which population means are significantly different from each other after the null hypothesis of equal population means is rejected in a one-factor ANOVA.

  • What is the null hypothesis in a one-factor ANOVA?

    -The null hypothesis in a one-factor ANOVA is that there is no regional difference among the population means, implying that all population means are the same.

  • What does it mean to 'reject the null hypothesis' in ANOVA?

    -Rejecting the null hypothesis in ANOVA means that there is statistical evidence to suggest that at least one of the population means is different from the others, given that the p-value is less than the significance level (e.g., 5%).

  • What is the significance of the p-value in ANOVA?

    -The p-value in ANOVA determines whether to reject or fail to reject the null hypothesis. If the p-value is less than the predetermined significance level, the null hypothesis is rejected, indicating a statistically significant difference between the group means.

  • What is the criterion used to compare the absolute mean differences in the Tukey method?

    -The criterion used in the Tukey method is the two-key criterion, which is calculated by multiplying the q-statistic from the studentized range distribution by the square root of the ratio of the mean square error to the sample size of the group with the least number of observations.

  • How is the sample size determined for the Tukey method when groups have different sizes?

    -When groups have different sample sizes, the Tukey method uses the sample size of the group with the least number of observations for the calculation of the two-key criterion.

  • What is the degrees of freedom used in calculating the Q statistic for the Tukey method?

    -The degrees of freedom for calculating the Q statistic in the Tukey method is the number of treatments (C) minus one for the numerator, and the total sample size (N) minus the number of treatments (C) for the denominator.

  • How do you find the critical value for the Q statistic in the Tukey method?

    -The critical value for the Q statistic is found by looking up the studentized range distribution with the appropriate degrees of freedom in the numerator and denominator, which can be found in statistical tables or online resources.

  • What does it mean if the absolute mean difference between two groups exceeds the two-key criterion?

    -If the absolute mean difference between two groups exceeds the two-key criterion, it indicates a statistically significant difference between the means of those two populations at the given significance level.

  • Why might there be a significant difference between some group means but not others, even if the overall ANOVA showed a significant effect?

    -This can occur because the overall ANOVA test is sensitive to any differences among group means, but the Tukey method specifically identifies which pairs of means are significantly different. It's possible for some pairs to differ significantly while others do not, reflecting the variability within the data.

  • How does statistical evidence from samples differ from mathematical reasoning in the context of ANOVA?

    -Statistical evidence from samples, as in ANOVA, can show differences between group means that may not logically follow from mathematical reasoning. For example, if no difference is found between groups 1 & 3 and 2 & 3, one might expect no difference between 1 & 2 either, but statistical analysis can reveal otherwise due to the variability and sample size.

Outlines
00:00
📊 Introduction to Tukey's Method for Post-ANOVA Analysis

This paragraph introduces the Tukey method for pairwise comparison of population means following a one-factor ANOVA. The null hypothesis of no regional difference among three population means is discussed, and the process of rejecting this hypothesis is explained. The video demonstrates how to proceed with Tukey's method if the null hypothesis is rejected, emphasizing the need for further analysis to identify which population means differ. The example dataset and ANOVA results are presented, showing a p-value less than the significance level, indicating a need for Tukey's method to compare sample means using absolute differences and a critical value from the studentized range distribution.

05:00
🔍 Detailed Steps of Tukey's Method Application

This paragraph provides a detailed walkthrough of applying Tukey's method. It explains the calculation of the absolute mean differences between pairs of sample means and compares these differences to a critical value derived from the studentized range distribution. The critical value is determined using degrees of freedom and mean square error from the ANOVA output. The example demonstrates the calculation with equal sample sizes for simplicity, and the process of finding the Q statistic using online resources is shown. The paragraph concludes with the comparison of mean differences to the critical value, revealing significant differences between certain population means and the lack thereof between others, highlighting the statistical evidence that may not align with mathematical expectations.

Mindmap
Keywords
💡Turkey Method
The Tukey method, also known as Tukey's Honest Significant Difference (HSD) test, is a statistical technique used for post-hoc pairwise comparisons of means after an ANOVA has shown a significant result. In the video, the Tukey method is central to identifying which population means are different from each other. The script explains that it is used after rejecting the null hypothesis in an ANOVA, to further analyze differences between the means of the groups.
💡Pairwise Comparison
Pairwise comparison refers to the process of comparing two groups at a time to determine if there is a significant difference between their means. The script mentions that the Tukey method is used for pairwise comparison of population means, which is essential for understanding the specific differences between groups after an ANOVA test has indicated an overall difference.
💡Null Hypothesis
The null hypothesis is a fundamental concept in statistical testing, typically stating that there is no difference between groups or variables being studied. In the context of the video, the null hypothesis is that there is no regional difference among the three population means. The script explains that if the null hypothesis is not rejected, no further analysis is needed, but if it is rejected, further analysis using the Tukey method is required.
💡ANOVA (Analysis of Variance)
ANOVA is a statistical method used to compare the means of three or more groups to determine if there are any statistically significant differences between them. The video script describes conducting an ANOVA to assess whether the population means from three populations are the same, with the p-value indicating the likelihood of the null hypothesis being true.
💡p-value
The p-value is a measure used in hypothesis testing to determine whether to reject the null hypothesis. A p-value less than a predetermined significance level (in the script, 5%) suggests that the null hypothesis is unlikely to be true. The script mentions that a p-value less than 5% leads to the rejection of the null hypothesis, triggering further analysis with the Tukey method.
💡Sample Means
Sample means refer to the average values calculated from the data of each group in a study. The video script discusses comparing the absolute differences between sample means of different groups as part of the Tukey method, which is crucial for identifying significant differences between group populations.
💡Critical Value
A critical value is a threshold used in hypothesis testing to determine the boundaries of the rejection region. In the script, the critical value from the studentized range distribution is used to compare with the absolute mean differences, helping to decide whether the differences between group means are statistically significant.
💡Degrees of Freedom
Degrees of freedom is a concept in statistics that denotes the number of independent values in a data set that are free to vary when calculating a statistic. The script explains that degrees of freedom are used to find the Q statistic from the studentized range distribution, which is essential for the Tukey method.
💡Mean Square Error
Mean square error (MSE) is a measure of the average squared difference between the observed values and the values predicted by a model or estimated by a statistical method. In the context of the video, MSE is used in the calculation of the Tukey criterion, which is part of the process to determine if the differences between group means are significant.
💡Significance Level
The significance level, often denoted as alpha, is the probability threshold for rejecting the null hypothesis in a statistical test. The script specifies a significance level of 5%, which is the standard for many statistical tests, indicating that any result with a p-value below this threshold is considered statistically significant.
💡Statistical Evidence
Statistical evidence refers to the results obtained from statistical tests that suggest a certain conclusion. The video script discusses how statistical evidence can sometimes differ from mathematical reasoning, as illustrated by the example where no difference is found between pairs 1 & 3 and 2 & 3, yet a significant difference is found between 1 & 2.
Highlights

Introduction of the Turkey method for pairwise comparison of population means in a one-factor ANOVA.

Explanation of when to conduct a post-ANOVA test: after rejecting the null hypothesis of no regional difference among population means.

Description of the null hypothesis in the context of ANOVA: no difference among the three population means.

Requirement for further analysis if the null hypothesis is rejected in ANOVA.

Use of a simple dataset to perform ANOVA to determine if population means are the same.

Presentation of ANOVA results with a p-value less than the significance level, leading to the rejection of the null hypothesis.

Introduction of the Tukey method for further inquiry after rejecting the null hypothesis.

Explanation of comparing sample means using their absolute differences.

Introduction of the two-key criterion for comparison, involving the q-statistic from the studentized range distribution.

Method to calculate the q-statistic using degrees of freedom and mean square error.

Use of the sample size of the group with the least number of observations in the calculation.

Procedure to find the Q statistic using critical values from the studentized range distribution.

Explanation of the degrees of freedom calculation for the Q statistic.

Identification of the mean square error from the ANOVA output for the Q statistic calculation.

Calculation of the absolute mean differences between sample means for each pair of groups.

Comparison of absolute mean differences to the critical two-key criterion to determine statistical significance.

Findings that show a significant difference between the means of populations 1 & 2, but not 1 & 3 or 2 & 3.

Discussion on the difference between statistical evidence and mathematical reasoning in the context of ANOVA results.

Conclusion of the presentation summarizing the use of the Tukey method in ANOVA.

Transcripts

Browse More Related Video

Tukey Kramer Multiple Comparison Procedure and ANOVA with Excel

Tukey-Kramer Post Hoc Test after One-Way ANOVA in Excel

Understanding Analysis of Variance (ANOVA) including Excel - Statistics Help

One Way ANOVA

Fisher's LSD Explained

ANOVA (Analysis of variance) simply explained

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ANOVATukey MethodStatistical AnalysisPost-Hoc TestMean ComparisonHypothesis TestingData InterpretationCritical ValueSample SizeStatistical SignificanceEducational Video