Rolle's Theorem to Prove Exactly one root for Cubic Function AP Calculus

Anil Kumar
8 Jan 201708:08
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Anil Kumar explains the application of Rolle's Theorem to prove that the cubic equation x^3 + x - 3 = 0 has exactly one real root. He first demonstrates the existence of at least one root by showing the function's value changes from negative to positive, indicating a zero crossing. Then, he uses a contradiction approach to prove the uniqueness of the root, showing that the derivative of the function is always positive, thus invalidating the assumption of multiple roots. The explanation is aimed at helping viewers understand the theorem's practical application in solving real-world problems.

Takeaways
  • 📚 The video discusses the application of Rolle's Theorem to prove the existence of a real root in the equation \( x^3 + x - 3 = 0 \).
  • 🔍 The first part of the explanation shows that the equation has at least one real root by evaluating the function at \( x = 0 \) and \( x = 2 \), observing a sign change from negative to positive.
  • 📈 The Intermediate Value Theorem is mentioned as an alternative approach to prove the existence of at least one real root due to the continuous nature of the polynomial function.
  • 🤔 The second part of the explanation aims to prove that there is exactly one real root, using a contradiction approach by assuming the existence of two real roots.
  • 📉 The contradiction arises when applying Rolle's Theorem, which requires the derivative of the function to be zero at some point between two roots, but the derivative \( 3x^2 + 1 \) is always positive.
  • 🚫 The assumption of two real roots leads to a contradiction because the derivative never equals zero, proving that there can only be one real root.
  • 📝 Rolle's Theorem conditions are reiterated: the function must be continuous, differentiable, and the function values at two points must be equal.
  • 📌 The derivative of the given function \( f'(x) = 3x^2 + 1 \) is shown to be always greater than or equal to one, hence never zero.
  • 🧩 The video concludes that the equation has exactly one real root, combining the proof of existence and uniqueness using mathematical reasoning.
  • 👨‍🏫 The presenter, Anil Kumar, provides a clear step-by-step explanation of the theorem's application and encourages viewers to share and subscribe to his videos.
  • 📚 The script is educational, focusing on a specific mathematical theorem and its practical application to solve a cubic equation.
Q & A

  • What theorem is being discussed in the video script?

    -The video script discusses the application of Rolle's Theorem.

  • What is the equation being analyzed in the script?

    -The equation being analyzed is x^3 + x - 3 = 0.

  • What are the two parts of the proof discussed in the script?

    -The two parts of the proof are: 1) showing that the equation has at least one real root, and 2) proving that it has exactly one real root.

  • How does the script demonstrate that the equation has at least one real root?

    -The script demonstrates this by evaluating the function at x = 0 and x = 2, showing a sign change from negative to positive, which implies the existence of at least one real root due to the Intermediate Value Theorem.

  • What is the Intermediate Value Theorem, and how is it applied here?

    -The Intermediate Value Theorem states that if a continuous function changes sign over an interval, then it must have a root within that interval. It is applied by observing the function values at x = 0 and x = 2, which change from negative to positive, indicating a root exists between these two points.

  • What is the contradiction approach used in the second part of the proof?

    -The contradiction approach assumes that there are two real roots of the equation and then uses Rolle's Theorem to find a point where the derivative is zero, which leads to a contradiction since the derivative is always positive.

  • What is the derivative of the function f(x) = x^3 + x - 3?

    -The derivative of the function is f'(x) = 3x^2 + 1.

  • Why is the assumption of two real roots a contradiction in this context?

    -The assumption leads to a contradiction because the derivative of the function is always positive, meaning it never crosses zero, which is a requirement for Rolle's Theorem to apply if there were two roots.

  • What conclusion can be drawn from the contradiction found in the derivative?

    -The conclusion is that the original assumption of two real roots is incorrect, and therefore, the equation has exactly one real root.

  • Who is the presenter of the video script?

    -The presenter of the video script is Anil Kumar.

  • What is the final message from the presenter to the audience?

    -The final message is a prompt for the audience to share and subscribe to the videos, and a thank you note from Anil Kumar.

Outlines
00:00
📚 Application of Rolle's Theorem to Prove Unique Real Root

In this paragraph, Amal Kumar introduces the application of Rolle's Theorem to demonstrate that the cubic equation X^3 + X - 3 = 0 has exactly one real root. The explanation is divided into two parts. The first part establishes the existence of at least one real root by showing that the function f(X) = X^3 + X - 3 changes sign from negative to positive as X varies from 0 to 2, implying a root must exist between these values due to the continuity and nature of polynomial functions. The second part of the explanation aims to prove the uniqueness of this real root, suggesting a contradiction approach by assuming the existence of two real roots and using Rolle's Theorem to show that this assumption leads to an impossibility, thus confirming the equation has only one real root.

05:04
🔍 Contradicting the Assumption of Multiple Real Roots

This paragraph delves into the contradiction method to prove the uniqueness of the real root for the given cubic equation. Assuming the function f(X) = X^3 + X - 3 has two real roots at points a and b, the speaker applies Rolle's Theorem, which requires the function to be continuous, differentiable, and to take the same value at two points (in this case, zero at both roots). The derivative f'(X) = 3X^2 + 1 is calculated and shown to be always positive, indicating that it cannot be zero, which contradicts the theorem's requirement for a point where the derivative is zero if there were two roots. This contradiction confirms that the original assumption of having two real roots is incorrect, and therefore, the equation indeed has exactly one real root. The explanation concludes with a reminder of the theorem's application and a sign-off from the speaker, Anil Kumar.

Mindmap
Keywords
💡Rolle's Theorem
Rolle's Theorem is a fundamental result in calculus that states if a function is continuous on a closed interval [a, b], differentiable on the open interval (a, b), and f(a) = f(b), then there exists at least one c in (a, b) such that the derivative of the function at c is zero. In the video, Rolle's Theorem is applied to prove that a given cubic function has exactly one real root, by showing that the derivative of the function is never zero, which contradicts the assumption of having more than one root.
💡Real Root
A real root of an equation is a value of the variable that makes the equation true when substituted into it. In the context of the video, the real root is a value of x that satisfies the cubic equation x^3 + x - 3 = 0. The video demonstrates that the function has at least one real root by showing the function's value changes from negative to positive, indicating it must cross the x-axis.
💡Polynomial
A polynomial is an algebraic expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The video discusses a cubic polynomial, x^3 + x - 3, and its properties, such as continuity and differentiability, which are essential for applying Rolle's Theorem.
💡Continuous Function
A continuous function is one where there are no abrupt changes in value, meaning the function can be drawn without lifting the pen from the paper. In the video, the continuity of the polynomial function is used to argue that it will cross the x-axis, as it changes from a negative value to a positive one, ensuring the existence of at least one real root.
💡Differentiable Function
A differentiable function is one for which the derivative exists at every point in its domain. The video script mentions that the function in question is differentiable on the interval (a, b), a condition necessary for applying Rolle's Theorem.
💡Intermediate Value Theorem
The Intermediate Value Theorem states that if a function is continuous on a closed interval and takes on two values, then it takes on every value between those two. The video suggests using this theorem to support the existence of a root, as the function values range from negative to positive, implying it must pass through zero.
💡Derivative
The derivative of a function measures the rate at which the function's output (or value) changes with respect to changes in its input. In the script, the derivative of the function f(x) = x^3 + x - 3 is calculated as f'(x) = 3x^2 + 1, which is used to show that the function is never flat, hence cannot have more than one real root.
💡Assumption
In the context of the video, an assumption is a hypothetical scenario proposed for the purpose of argument. The script begins with the assumption that the function has two real roots, which is later contradicted to prove that the function has exactly one real root.
💡Contradiction
A contradiction occurs when an argument or statement leads to a logical inconsistency or a situation that cannot be true. The video uses a contradiction by assuming two real roots and then showing that this would imply the derivative is zero at some point, which is not the case, thus proving the original assumption is false.
💡Cubic Function
A cubic function is a type of polynomial function of degree three. The video focuses on the cubic function f(x) = x^3 + x - 3, analyzing its properties to demonstrate the existence and uniqueness of its real roots.
💡Value Change
Value change refers to the transition of a function's output from one value to another. The script discusses the change in the function's value from negative to positive, which is crucial for establishing the existence of a real root using the Intermediate Value Theorem.
Highlights

Application of Rolle's theorem to prove the equation x^3 + x - 3 = 0 has exactly one real root.

The approach is divided into two parts: first, proving the existence of at least one root, and second, proving there is only one real root.

Use of the Intermediate Value Theorem as an alternative method to prove the existence of at least one root.

Demonstration that the function f(x) = x^3 + x - 3 is continuous and changes sign from negative to positive, indicating at least one real zero.

Assumption for contradiction: assuming the function has two real roots at x = a and x = b.

Application of Rolle's Theorem under the assumption of two real roots, implying there must be a point c where the derivative is zero.

Derivative of the function f'(x) = 3x^2 + 1 is always positive, contradicting the assumption of two real roots.

The derivative's constant positivity proves the incorrectness of the assumption that the function has two real roots.

Final conclusion that the given equation has exactly one real root based on the contradiction.

Introduction of the function f(x) = x^3 + x - 3 and its properties for the analysis.

Explanation of the continuous nature of polynomials and their implications for root existence.

Calculation of f(0) and f(2) to demonstrate the function's value change from negative to positive.

Discussion on the coverage of all values by a continuous function between two points.

Use of the Intermediate Value Theorem to support the existence of at least one real zero.

Introduction of the contradiction method to prove the uniqueness of the real root.

Detailed explanation of the conditions required for Rolle's Theorem to apply.

Finding the derivative of the function and its implications for the proof.

Instructor Anil Kumar's closing remarks and invitation to share and subscribe to his videos.

Transcripts

Browse More Related Video

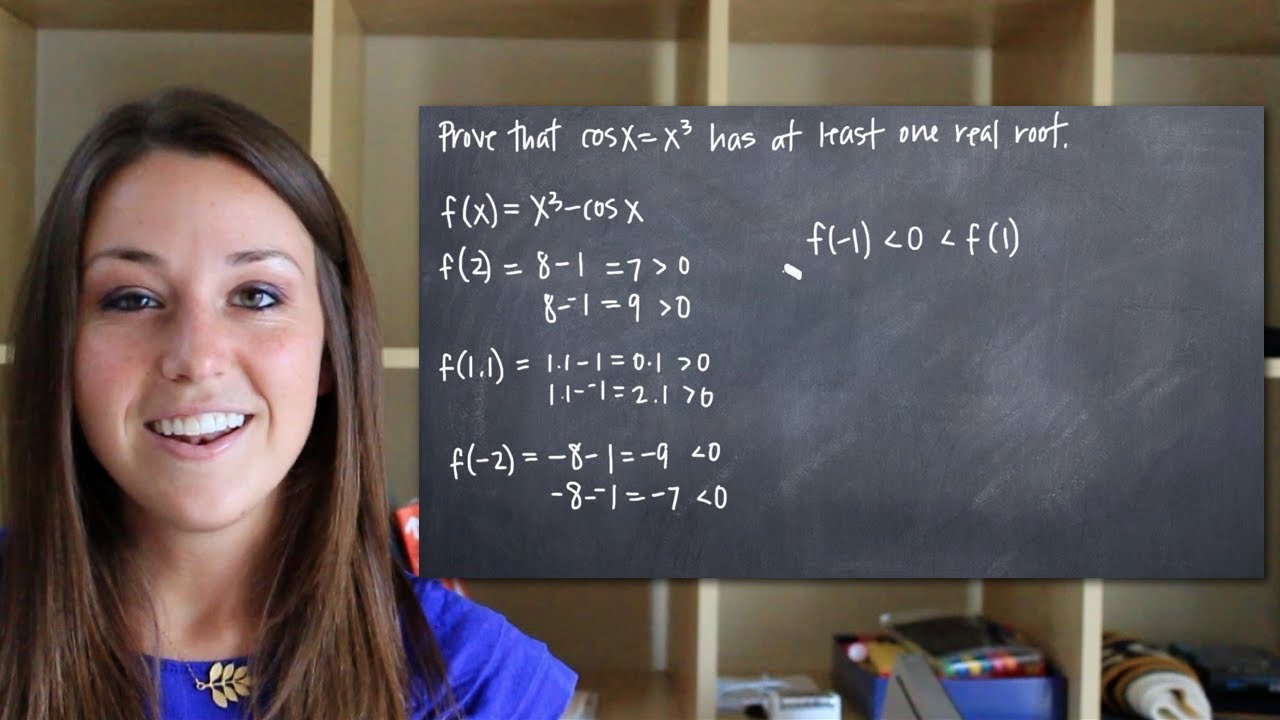
Prove the equation has at least one real root (KristaKingMath)

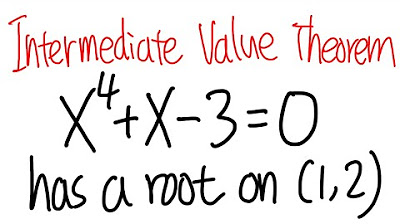
Intermediate Value Theorem, calculus 1 tutorial, showing a root of a function on an interval

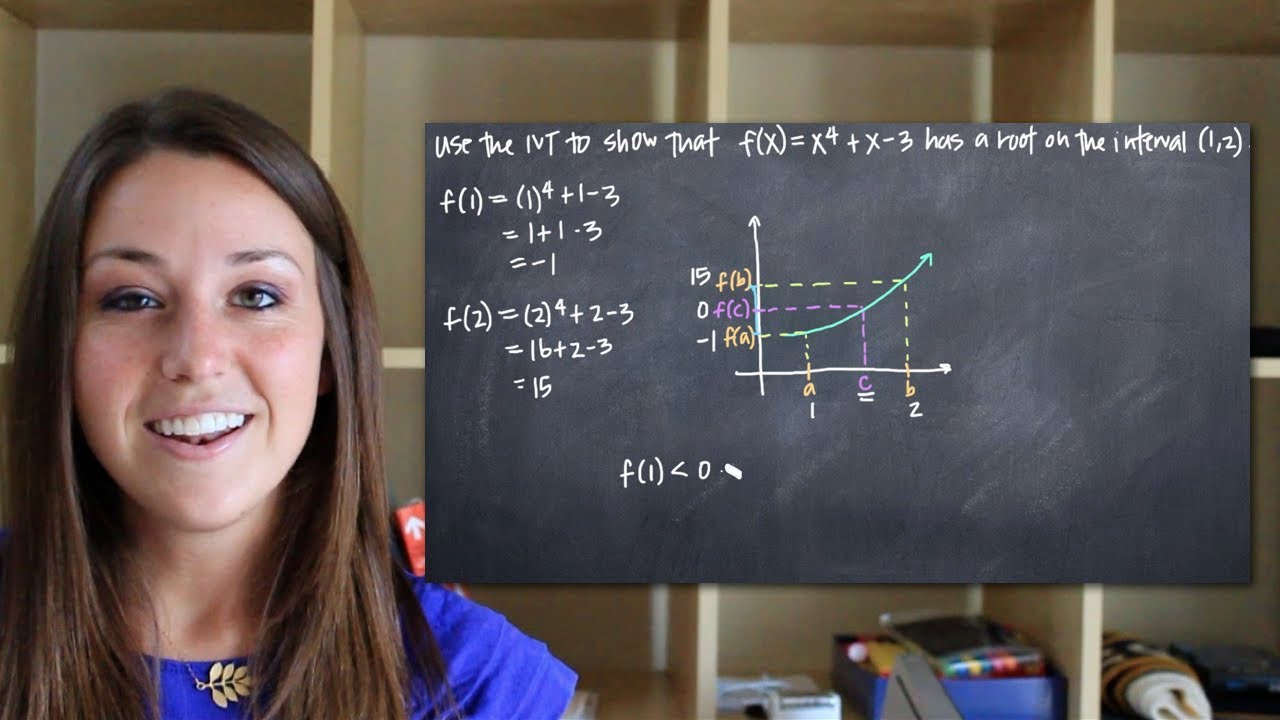
Intermediate value theorem to prove a root in an interval (KristaKingMath)

Intermediate Value Theorem: show function has at least one solution -- CALCULUS

How to show that a solution exists to a functions using IVT

❖ The Mean Value Theorem ❖

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Rolle's TheoremCubic EquationReal RootMathematicsProof MethodContinuous FunctionDerivativeIntermediate ValueRoot AnalysisTheoretical MathEducational Video