Normal Distribution: Calculating Probabilities {TI 84 Plus CE}

Bell Curved Education
6 May 201706:46
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial demonstrates how to use the Texas Instruments TI-84 Plus C calculator to calculate probabilities within a normal distribution. It explains the concept of probabilities as areas under the curve and guides through the process of finding the probability of a cookie having between 8 and 14 chocolate chips, given a mean of 12 and a standard deviation of 2.2. The video also shows how to calculate probabilities for values below or above a certain threshold using the normal CDF function, emphasizing the use of extremely small or large numbers for infinite bounds.

Takeaways
  • 📚 The tutorial is about using the Texas Instruments TI-84 Plus C calculator to find integral and non-integral probabilities of a normal distribution.
  • 📈 Understanding normal distribution involves recognizing that 99.77% of data fits within three standard deviations, with the mean at the center.
  • 🍪 The video uses a baking cookies analogy to explain the concept, where the number of chocolate chips per cookie represents the data points.
  • 📊 The mean is set to twelve, and the standard deviation is two point two, aiming for each cookie to have between 8 and 14 chocolate chips.
  • 🔢 To calculate probabilities, the video instructs to use the calculator's distribution section, specifically the normal CDF function.
  • 📝 The process involves inputting the lower and upper bounds, mean, and standard deviation into the calculator to find the probability of a data point falling within a range.
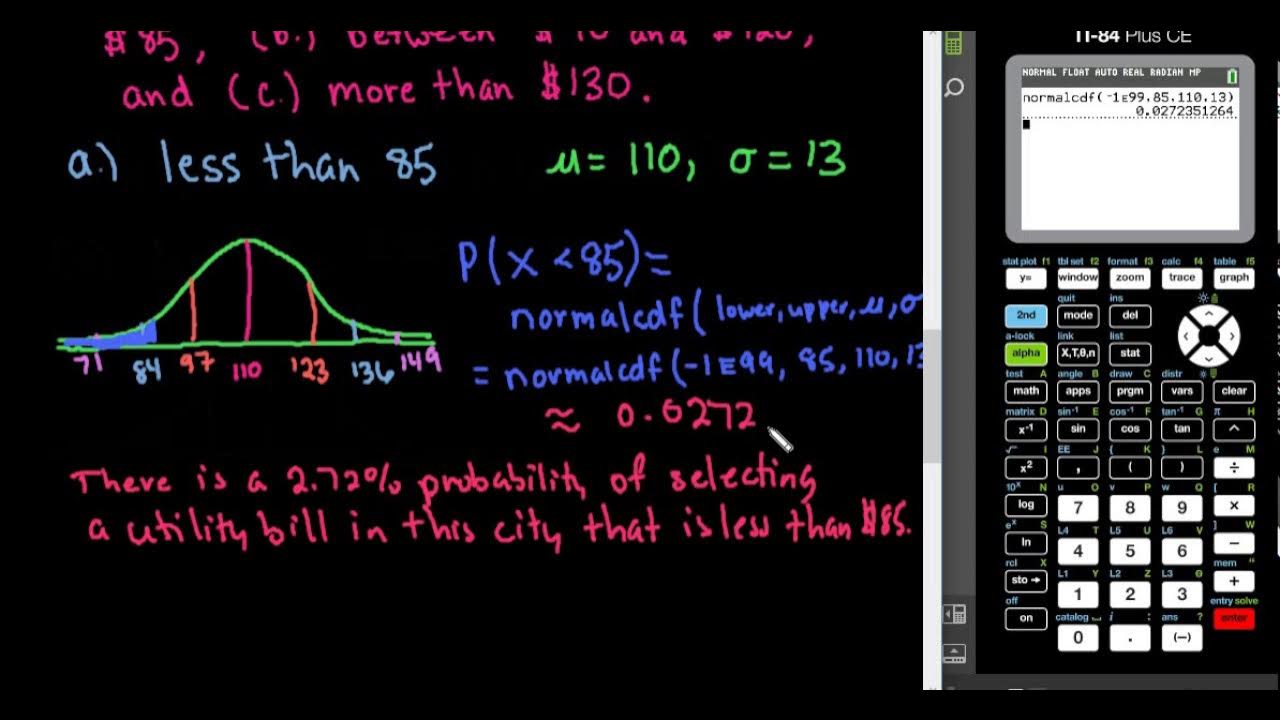
  • 💡 The probability of a cookie having between 8 and 14 chocolate chips is approximately 78%, indicating the area under the graph for this range.
  • 🤔 For non-integral probabilities, such as the chance of having less than 6 chocolate chips, the calculator uses a very small number as the lower bound.
  • 🔍 The calculator's normal CDF function is used again, but with adjustments for the bounds to reflect the desired probability calculation.
  • 📉 To find the probability of an event with no upper limit, like having more than 14 chocolate chips, a very large number is used as the upper bound.
  • 📝 The video concludes by emphasizing the importance of identifying the mean, standard deviation, and graph limits for calculating probabilities under a normal distribution.
Q & A

  • What is the purpose of the tutorial video?

    -The tutorial video is designed to teach viewers how to use a Texas Instruments TI-84 Plus C calculator to find integral and non-integral probabilities of a normal distribution.

  • What does the term 'normal distribution' refer to in the context of the video?

    -In the video, 'normal distribution' refers to a type of distribution in statistics that is symmetrical and where data points are clustered around the mean, with the majority of the data falling within three standard deviations from the mean.

  • What is the significance of the number 99.77% in the context of normal distribution?

    -The number 99.77% signifies that in a perfectly normally distributed set of data, almost all of the data points (99.77%) fall within three standard deviations of the mean.

  • What is an example used in the video to explain normal distribution?

    -The video uses the example of baking cookies to explain normal distribution, where the number of chocolate chips on each cookie represents the data points, and the mean and standard deviation are used to describe the distribution of these points.

  • What is the mean and standard deviation of the chocolate chips in the cookie example?

    -In the cookie example, the mean number of chocolate chips is 12, and the standard deviation is 2.2.

  • What is the range of chocolate chips per cookie that the viewer is trying to calculate the probability for?

    -The viewer is trying to calculate the probability for the range of 8 to 14 chocolate chips per cookie.

  • How does the video guide the viewer to calculate the probability of a specific range using the calculator?

    -The video instructs the viewer to use the 'normal CDF' function on the TI-84 Plus C calculator, input the lower and upper bounds, the mean, and the standard deviation, and then execute the calculation to find the probability.

  • What does the probability of approximately 0.78 signify in the context of the cookie example?

    -The probability of approximately 0.78 means there is about a 78% chance that a randomly selected cookie will have between 8 and 14 chocolate chips.

  • How does the video explain calculating the probability for non-integral values, such as less than 6 chocolate chips?

    -The video demonstrates using the 'normal CDF' function with a very small number as the lower bound to approximate the probability of a value less than a certain number, such as less than 6 chocolate chips.

  • What is the significance of the values 'negative 1 to the 99' and 'positive 1 to the 99' in the calculator?

    -The values 'negative 1 to the 99' and 'positive 1 to the 99' are used in the calculator to represent extremely small and large numbers, respectively, for calculating probabilities when there is no lower or upper limit to the data range.

  • What is the probability of having a cookie with more than 14 chocolate chips, according to the video?

    -The video calculates the probability of having a cookie with more than 14 chocolate chips to be approximately 0.18.

Outlines
00:00
📊 Understanding Normal Distribution Probabilities

This paragraph introduces a tutorial on using the Texas Instruments TI-84 Plus C calculator to calculate integral and non-integral probabilities of a normal distribution. It explains the concept of normal distribution with the help of an analogy involving baking cookies and the number of chocolate chips per cookie. The mean and standard deviation are defined, and the importance of calculating the probability of a data point falling within a specific range is emphasized. The paragraph guides the user on how to input values into the calculator to find the probability of a cookie having between 8 and 14 chocolate chips, which is approximately 78%.

05:00
🔢 Calculating Tail Probabilities with the Calculator

The second paragraph continues the tutorial by explaining how to calculate tail probabilities using the normal CDF function on the calculator. It describes how to find the probability of a cookie having less than 6 chocolate chips by setting the lower bound to a very small number and the upper bound to 6. The tutorial also covers how to calculate the probability of a value exceeding a certain threshold, such as more than 14 chocolate chips, by setting the lower bound to that threshold and the upper bound to a very large number. The paragraph concludes with a summary of the necessary steps and inputs for calculating probabilities under a normal distribution, including identifying the mean, standard deviation, and setting the appropriate bounds for the calculator.

Mindmap
Keywords
💡Texas Instruments TI-84 Plus C
The Texas Instruments TI-84 Plus C is a graphing calculator designed for advanced mathematical computations. In the video, it is the central tool used to demonstrate how to calculate probabilities related to a normal distribution. The script mentions it as the device that will be used to find integral and non-integral probabilities, indicating its capability to handle complex statistical functions.
💡Normal Distribution
A normal distribution, also known as Gaussian distribution, is a probability distribution that is characterized by a symmetrical bell-shaped curve. The video script explains that the normal distribution is important for understanding the probabilities of data points within a set range, such as the number of chocolate chips on cookies in the provided example.
💡Integral and Non-Integral Probabilities
Integral probabilities refer to the area under the curve of a normal distribution between two given points, while non-integral probabilities include the endpoints. The script discusses how to calculate both types of probabilities using the TI-84 Plus C calculator, which is essential for understanding the likelihood of certain outcomes within a normal distribution.
💡Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. In the context of the video, the standard deviation is used to define the spread of the normal distribution, with the script mentioning it as 2.2 for the chocolate chips example, indicating how much the number of chips can vary from the mean.
💡Mean
The mean, often referred to as the average, is the sum of all values in a data set divided by the number of values. The script uses the mean to represent the central value of the normal distribution, with the example of 12 chocolate chips per cookie, serving as the reference point for calculating probabilities.
💡Three Standard Deviations Rule
The three standard deviations rule states that in a normal distribution, approximately 99.77% of the data falls within three standard deviations of the mean. The script refers to this rule to emphasize the significance of the standard deviation in understanding the distribution of data points.
💡Probability
Probability is a measure of the likelihood that a particular event will occur. The video script discusses calculating probabilities within a normal distribution as the area under the curve between certain bounds, such as the likelihood of a cookie having between 8 and 14 chocolate chips.
💡Area Under the Curve
In the context of a normal distribution, the area under the curve represents the probability of a data point occurring within a specified range. The script explains how to calculate this area using the TI-84 Plus C calculator to find the probability of events, such as the number of chocolate chips on a cookie.
💡Normal CDF (Cumulative Distribution Function)
The normal cumulative distribution function (CDF) calculates the probability that a normally distributed random variable is less than or equal to a certain value. The script instructs how to use the TI-84 Plus C calculator's normal CDF function to find the probability of a value falling within a specific range, such as the number of chocolate chips on cookies.
💡Lower and Upper Bounds
Lower and upper bounds define the range within which probabilities are calculated. The script uses these terms to specify the range of chocolate chips on cookies (8 to 14) and explains how to input these bounds into the calculator to find the probability of a cookie falling within this range.
💡E to the Power of 99
In the script, 'e to the power of 99' is used to represent extremely large or small numbers when calculating probabilities with no upper or lower limits. The script mentions using negative 1 to the power of 99 for a very small number and positive 1 to the power of 99 for a very large number, which helps in calculating probabilities that extend to the tails of the normal distribution.
Highlights

Tutorial on using Texas Instruments TI-84 Plus C to find integral and non-integral probabilities of a normal distribution.

Explanation of what integral and non-integral probabilities mean in terms of a normal distribution graph.

Understanding that 99.77% of data fits within three standard deviations in a normal distribution.

Mean is in the middle of a perfectly normally distributed graph.

Illustrative example of baking cookies to explain the concept of standard deviation and mean.

Using the normal distribution to determine the number of cookies with a specific range of chocolate chips.

Introduction to the calculator's distribution section for calculating probabilities.

How to use the normal CDF function on the TI-84 Plus C calculator.

Setting the lower and upper bounds for calculating the probability of a specific range.

Entering the mean and standard deviation values for the normal distribution calculation.

Calculating the probability of a cookie having between 8 and 14 chocolate chips.

Interpreting the result showing approximately 78% chance for the desired chocolate chip range.

Adjusting the calculator for calculating the probability of less than a certain number of chocolate chips.

Using negative 1 to the power of 99 to represent a very small number in the calculator.

Calculating the probability of having fewer than 6 chocolate chips in a cookie.

Understanding the result of approximately 0.32% chance for less than 6 chocolate chips.

Guidance on how to calculate probabilities with no upper or lower limits using very large or small numbers.

Using positive 1 to the power of 99 to represent an infinitely large number in the calculator.

Calculating the probability of a cookie having more than 14 chocolate chips.

Interpreting the result showing approximately 18% chance for more than 14 chocolate chips.

Summary of the key information needed for calculating probabilities under a normal distribution.

Transcripts

Browse More Related Video

Probabilities in a Normal Distribution - TI-84

Math 119 Chap 6 part 1

Finding the Area Under a Standard Normal Curve Using the TI-84

Probabilities from density curves | Random variables | AP Statistics | Khan Academy

Math 119 Chap 6 part 3

Standard Normal Distribution Tables, Z Scores, Probability & Empirical Rule - Stats

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Normal DistributionTI-84 Plus CCalculus TutorialProbability CalculationStandard DeviationMean ValueGraph AnalysisBaking AnalogyStatistical LearningEducational Content