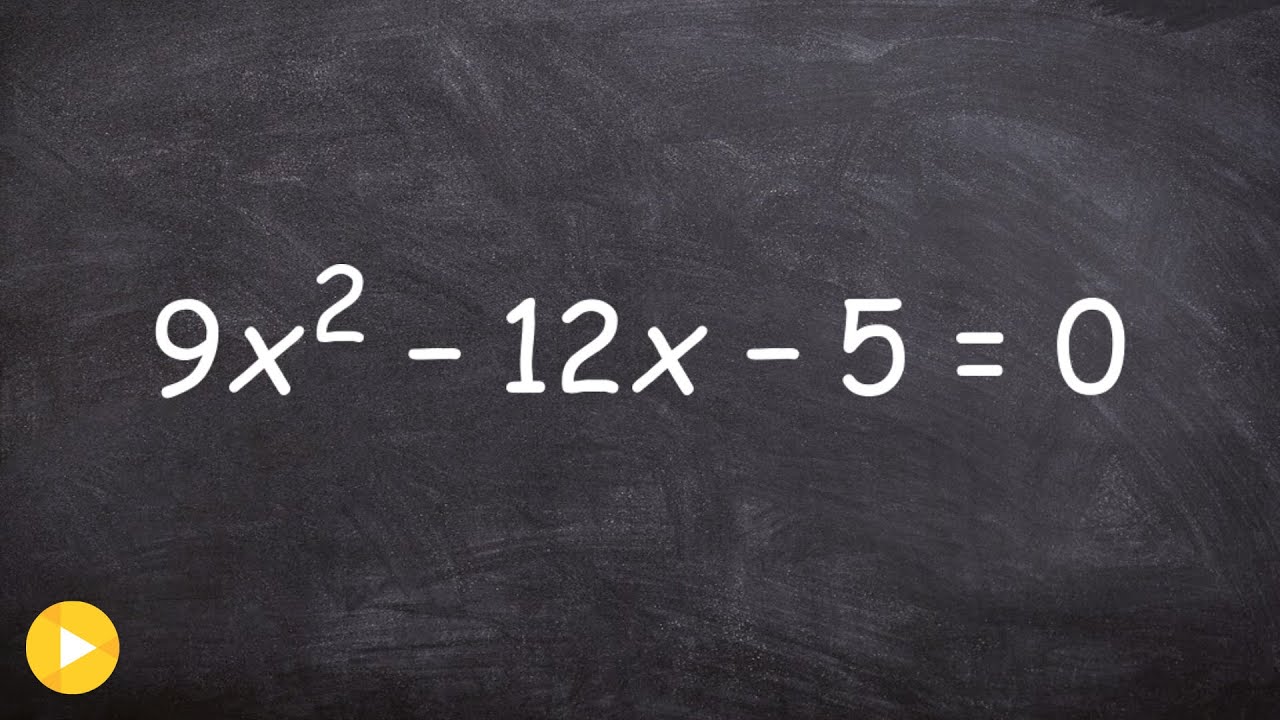factoring trinomials with "a" greater than 1
TLDRThis educational video script focuses on factoring trinomials in the form ax^2 + bx + c, particularly when 'a' is greater than one. It emphasizes the importance of identifying common factors and the process of factoring by grouping. The script outlines a step-by-step method, starting with multiplying the leading coefficient by the constant, listing factors, and then strategically splitting the middle term. It provides clear rules for adding or subtracting terms based on the sign of the last term, leading to a familiar factor by grouping approach. The process concludes with pulling out common factors and simplifying the expression, demonstrating a systematic method that requires mathematical skills rather than guesswork.
Takeaways
- 📚 The lesson is about factoring trinomials in the form ax^2 + bx + c, emphasizing that 'a' being greater than one is a key indicator to use this method.
- 🔍 The first step is to check for a common factor in all three terms, which in this case, does not exist.
- 🔑 The exponent of 'x' in the quadratic term is twice the exponent in the linear term, which is crucial for the factoring process.
- 📝 The process begins by copying the first and last terms and preparing to factor by grouping.
- 🤔 The leading coefficient (a) is multiplied by the constant (c) to find a product, in this case, 2 * 15 = 30.
- 🔢 A list of all factors of the product (30) is made to determine how to split the middle term, which in this case is 13.
- ➕ A rule is introduced: if the last term has a '+', the factors are added to the middle term, otherwise, they are subtracted.
- 🔄 The middle term is split into two factors that add up to the desired number (13), choosing factors that adhere to the rule mentioned.
- 🔄 The trinomial is then factored by grouping, circling the first two and last two terms.
- 🌀 Common factors are pulled out from each group, in this case, 'x' from the first group and '5' from the second.
- 📉 After pulling out common factors, a common binomial factor (2x + 3) is identified in the remaining terms.
- 🎯 The final step is to factor out the common binomial, resulting in a factored form that can be verified by foiling it back to the original trinomial.
Q & A
What is the topic of the video script?
-The topic of the video script is factoring trinomials in the form ax^2 + bx + c, specifically when 'a' is greater than one.
What is the first step suggested in the script for factoring a trinomial?
-The first step is to check if there is a common factor that can be pulled out from all three terms of the trinomial.
Why is it important to check the exponent of 'a' when factoring trinomials?
-It is important because if the exponent of 'a' is twice the exponent of the middle term, it indicates that the trinomial can be factored using the method described in the script.
What is the significance of the number 'a' being greater than one in the context of this script?
-When 'a' is greater than one, it suggests that the trinomial can be factored using the specific method discussed in the script, which involves factoring by grouping.
What is the FOIL method mentioned in the script?
-The FOIL method is a technique used for multiplying two binomials, which is related to the final form the trinomial can be factored into, as mentioned in the script.
How does the script suggest to handle the middle term when factoring trinomials?
-The script suggests splitting the middle term into two factors that add up to the original middle term's coefficient, based on the factors of the product obtained by multiplying the first and last terms.
What rule does the script provide for determining whether to add or subtract the two factors of the middle term?
-The rule is to add the two factors if there is a plus sign in the last term of the trinomial, and to subtract them if there is a minus sign.
What is the process of 'factor by grouping' as described in the script?
-The process involves circling the first two terms and the last two terms, pulling out common factors from each group, and then checking if the remaining terms can be factored further, ultimately resulting in a binomial.
How does the script ensure that the factoring process is correct?
-The script suggests visually checking the multiplication of the terms to ensure that they match the original trinomial and that the parentheses match after factoring.
What is the final result of the factoring process as described in the script?
-The final result is a binomial multiplied by another binomial, which is the factored form of the original trinomial.
Does the script suggest any guesswork or checking during the factoring process?
-No, the script emphasizes that the factoring process relies solely on math skills and does not involve guesswork or checking.
Outlines
📚 Factoring Trinomials with 'a' Greater Than One
This paragraph introduces the method of factoring trinomials in the form ax^2 + bx + c, where 'a' is greater than one. The speaker emphasizes that the first step is to check for a common factor in all three terms, which is not present in this case. The focus then shifts to recognizing the pattern that allows for factoring, specifically when the exponent of 'a' is twice the exponent of the middle term. The process involves multiplying the leading coefficient by the constant, listing all factors of the product, and then splitting the middle term into two parts that sum up to the original middle coefficient. The decision to add or subtract these parts is determined by the sign of the constant term. The paragraph concludes with the application of factor by grouping, where common factors are pulled out from groups of terms, leading to the final factored form.
🔍 Detailed Factoring Process and Verification
The second paragraph delves deeper into the factoring process, starting with the verification of the middle term's factorization. It explains the importance of identifying the correct pair of factors that add up to the middle coefficient, especially when the last term is positive. The speaker uses the example of choosing between adding or subtracting factors of 30 to achieve the middle term of 13. The paragraph then illustrates the factor by grouping method, where the first and last terms are grouped and common factors are extracted. The process continues with identifying a common binomial factor in the remaining terms and pulling it out to the front, resulting in a final factored form. The speaker also suggests spacing out the factors for clarity and emphasizes that the method is based on mathematical skills rather than guesswork.
Mindmap
Keywords
💡Factoring
💡Trinomial
💡Common Factor
💡Exponent
💡FOIL
💡Leading Coefficient
💡Factors of 30
💡Middle Term
💡Factor by Grouping
💡Binomial
💡Parentheses
Highlights
Introduction to factoring trinomials in the form ax^2 + bx + c, emphasizing the importance of 'a' being greater than one.
Initial step of checking for a common factor in the trinomial and finding none.
Observation that the exponent of 'a' is twice the exponent of 'c', which facilitates the factoring process.
Method of copying the first and last terms and preparing to factor by grouping.
Multiplication of the leading coefficient and constant to find a common product.
Listing all factors of the common product to assist in the factoring process.
Explanation of splitting the middle term into two factors that sum to a specific number.
Rule for determining whether to add or subtract the two factors based on the sign of the last term.
Selection of factors that add up to the middle term based on the rule provided.
Visual confirmation of the selection of factors to ensure they add up correctly.
Transition to factor by grouping, a method previously discussed.
Step-by-step guide on factoring by grouping, starting with circling the first two terms and the last two terms.
Identification of a common letter (x) in the first grouping and factoring it out.
Search for a common factor in the second grouping and factoring out the number 5.
Recognition of a common binomial factor in the remaining terms after factoring out.
Pulling out the common binomial factor and leaving a simple binomial inside the parentheses.
Final step of completing the factoring process and presenting the factored form.
Optional step of rewriting the factored form more spaced out for clarity.
Emphasis on the ease of the factoring process when following the outlined steps without guesswork.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: