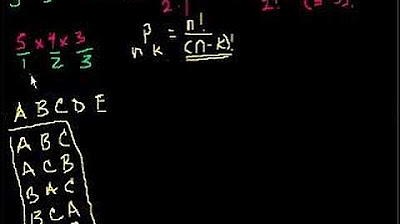4.4.5 Counting - Permutations and Combinations and the Combinations Rule
TLDRThis video script delves into the concepts of permutations and combinations, highlighting their differences and applications. It uses the Olympics medal scenario to illustrate permutations, where order matters, and committees to represent combinations, where it does not. The script explains the formula for calculating combinations, emphasizing its similarity to the permutations formula but with an additional factor to account for the irrelevance of order. An example of the California Fantasy 5 lottery game is provided to demonstrate the calculation of combinations intuitively and through the formula, revealing the vast number of possible tickets and the minuscule probability of winning, which humorously underscores the lottery as a 'tax on poor math skills.'
Takeaways
- 📚 The lesson is focused on understanding permutations and combinations, emphasizing their differences and applications.
- 🏅 Permutations are arrangements where order matters, exemplified by the Olympic medal rankings where the position is significant.
- 🎓 Combinations are like forming committees where the order of selection does not affect the group's identity, regardless of the order of members.
- 🔢 The combination formula is derived from the permutation formula, with an additional 'r factorial' in the denominator to account for the disregard of order.
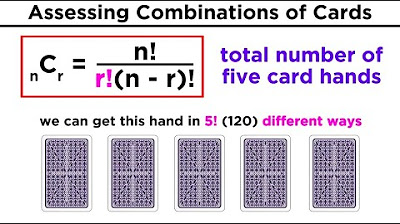
- 📈 The combination formula is \( \frac{n!}{(n-r)!r!} \), where 'n' is the total number of items and 'r' is the number of items selected without replacement.
- 🧠 The script provides an intuitive approach to understanding combinations, explaining why we divide by 'r factorial' to correct for overcounting arrangements.
- 🎰 An example of a real-world application is the California Fantasy 5 lottery, where the order of winning numbers does not affect the outcome.
- 🤔 The script discusses calculating the number of possible lottery tickets and the probability of winning the jackpot with a single ticket purchase.
- 📉 It is highlighted that the probability of winning the jackpot is extremely low, emphasizing the small odds of 1 in 575,757.
- 💡 The transcript also touches on the practical implications of these odds, suggesting that buying multiple tickets does not significantly increase the chances of winning.
- 🗣️ The author of the textbook is quoted, noting that lotteries often rely on people's lack of understanding of probabilities, with a humorous but critical comment on the 'lottery as a tax on people who are bad at math'.
Q & A
What is the main topic of the video?
-The main topic of the video is understanding the difference between permutations and combinations, with a focus on the concept of combinations and how to calculate them.
What is the key difference between permutations and combinations?
-The key difference is that permutations deal with the order of items, meaning the position matters, while combinations do not consider the order, only the selection of items.
Can you provide an example of permutations from the video?
-An example of permutations given in the video is the order of medals awarded at the Olympics, where the order of receiving gold, silver, or bronze matters.
How are combinations illustrated in the video with a real-life example?
-Combinations are illustrated with the example of forming a committee, where the order of selecting members does not matter, and the same group of people constitutes the same committee regardless of the order they were chosen in.
What is the formula used to calculate combinations?
-The formula used to calculate combinations is n! / [(n-r)! * r!], where n is the total number of items, r is the number of items selected, and '!' denotes factorial.
How does the video explain the intuitive approach to understanding combinations?
-The video explains the intuitive approach by first calculating the total number of ways to choose items without considering order, and then dividing by the factorial of the number of items chosen to correct for overcounting due to different arrangements of the same selection.
What is the California Fantasy 5 lottery game mentioned in the video?
-The California Fantasy 5 is a lottery game where players select five different numbers from 1 to 39, and winning the jackpot requires matching the drawn numbers regardless of the order.
How many different lottery tickets are possible in the Fantasy 5 game according to the video?
-There are 575,757 different possible lottery tickets in the Fantasy 5 game.
What is the probability of winning the jackpot with one ticket purchased, as discussed in the video?
-The probability of winning the jackpot with one ticket purchased is 1 in 575,757.
What additional insight does the video provide regarding playing the lottery?
-The video suggests that buying one ticket gives a very small chance of winning, and buying more tickets does not significantly increase the chances due to the low probability, implying that it might not be a good investment.
What is the humorous remark made by the author of the textbook in the video?
-The humorous remark is that some people say the lottery is a tax on people who are bad at math, highlighting the very low probability of winning and the lack of understanding of this probability by many participants.
Outlines
🔑 Understanding Permutations and Combinations
This paragraph introduces the concept of permutations and combinations, focusing on the difference between them. Permutations are arrangements where order is significant, exemplified by the Olympic medal rankings. Combinations, however, are like forming committees where the order of selection does not matter. The paragraph explains the combination rule for counting without replacement and introduces the formula for calculating combinations, which differs from the permutations formula by the inclusion of an additional r factorial in the denominator. An intuitive approach and a formulaic approach are both discussed to understand why the formula is structured as it is.
🎰 Applying Combinations to the Fantasy 5 Lottery
The second paragraph delves into an example using California's Fantasy 5 lottery game to illustrate the concept of combinations. It explains that winning the jackpot involves selecting five different numbers from a pool of 1 to 39, where the order of selection does not impact the outcome. The paragraph outlines an intuitive method for calculating the total number of possible lottery tickets by considering the decreasing number of options with each selection. It also discusses the overcounting issue and the necessity of dividing by five factorial to correct for it, resulting in 575,757 possible combinations. The paragraph concludes by showing that using the combinations formula yields the same result, reinforcing the understanding of the concept.
📉 Calculating the Probability of Winning the Jackpot
The final paragraph addresses the probability of winning the jackpot with a single ticket purchase in the context of the lottery example. It calculates the probability as one in 575,757, highlighting the extremely low odds of winning. The paragraph also touches on the psychological aspect of lottery participation, noting that people often lack an understanding of these probabilities and may not appreciate the improbability of winning. It humorously suggests that buying two tickets does not significantly improve one's chances and ends with a cautionary note about the lottery being a 'tax on people who are bad at math,' advising to play responsibly with a single ticket.
Mindmap
Keywords
💡Permutations
💡Combinations
💡Position
💡Mnemonic
💡Factorial
💡Selection without replacement
💡Combination Rule
💡Intuitive Approach
💡Formulaic Approach
💡Lottery
💡Probability
Highlights
Understanding the difference between permutations and combinations is crucial.
Permutations deal with the order of items, while combinations do not.
An example of permutations is the order of medals awarded at the Olympics.
Combinations are analogous to forming committees where order does not matter.
The combination rule for counting is introduced with a formula.
The formula for combinations is a modification of the permutations formula.
Combinations are used for arrangements where order is irrelevant.
An intuitive approach and a formulaic approach are both discussed for understanding combinations.
The California Fantasy 5 lottery game is used as an example to illustrate combinations.
The number of different lottery tickets possible is calculated using the combinations formula.
The probability of winning the jackpot with one ticket is extremely low.
The value of the winning probability is emphasized to highlight the low odds.
Lotteries capitalize on people's lack of understanding of small probabilities.
The saying 'lottery is a tax on people who are bad at math' is mentioned.
Buying multiple lottery tickets does not significantly increase the chance of winning.
A recommendation is made to only buy one lottery ticket due to the low odds.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: