01 - What is a Permutation? Learn the Permutation Formula.
TLDRThis tutorial introduces students to the concepts of probability and statistics, focusing on the often misunderstood topic of permutations. The instructor emphasizes the importance of order in permutations, contrasting it with combinations where order doesn't matter. Through various examples, including arranging letters, choosing race winners, and selecting officers from a group, the video demonstrates the use of the fundamental counting principle and the nPr formula to calculate permutations. The clear explanations and step-by-step approach aim to demystify permutations and build a strong foundation for further statistical learning.
Takeaways
- 📚 The tutor is excited to teach probability and statistics, covering a wide range of topics in these subjects.
- 🧩 People often struggle with probability and statistics due to the abstract nature of word problems and the need to extract and interpret information.
- 🔢 The fundamental difference between algebra and probability is that the latter deals with uncertain outcomes and probabilities rather than concrete solutions.
- 🎯 The tutor emphasizes the importance of understanding permutations as an ordering of events where the sequence is crucial.
- 🌳 The use of tree diagrams is introduced as a methodical way to visualize and list all possible permutations without missing any.
- 🏁 An example of a marathon race is used to illustrate how permutations work, with different winners for first and second place creating various outcomes.
- 🤔 The tutor encourages students to think logically and methodically when approaching probability problems, much like constructing a tree diagram.
- 🎓 The Fundamental Counting Principle is introduced as a mathematical concept to calculate the total number of ways a sequence of events can occur by multiplying the number of possibilities for each event.
- 📈 The script uses the example of choosing a President, Vice President, and Secretary from 20 candidates to demonstrate the application of the Fundamental Counting Principle.
- 📝 The notation nPr is explained as a shorthand for permutations of n elements taken r at a time, which is calculated as n! / (n-r)!
- 📲 The tutor advises that for permutation problems, one should first try to use the Fundamental Counting Principle and then consider using permutation formulas if necessary or instructed.
Q & A
What is the main focus of the probability and statistics tutor's class?
-The main focus of the class is to teach probability first and then move on to statistics, covering most of the topics students will encounter in their class.
Why do many people have problems with probability and statistics?
-Many people have problems with probability and statistics because the problems are usually word problems that require interpretation and logical thinking, unlike the more mechanical nature of problems in subjects like algebra.
What is the fundamental difference between probability and traditional math problems?
-The fundamental difference is that probability deals with the likelihood of events occurring rather than concrete numbers, making it less rigid and more uncertain compared to traditional math problems.
What is a permutation and why is it important in probability?
-A permutation is an ordering of events where the order matters. It is important in probability because it helps in determining the different possible outcomes of an event occurring in a specific order.
Can you give an example of how permutations are used in a real-world scenario as described in the script?
-An example given in the script is a marathon race with four participants where the order of finish matters. The permutations help in determining the different possible ways the first and second place winners can occur.
What is the Fundamental Counting Principle and how is it applied in the script?
-The Fundamental Counting Principle states that if there are a series of events, the total number of ways all events can occur is the product of the number of ways each individual event can occur. In the script, it is applied to calculate the total number of permutations in a race and other examples.
How does the script demonstrate the use of a tree diagram to solve permutation problems?
-The script demonstrates the use of a tree diagram by constructing an example where it lists all possible outcomes for the first and second place winners in a marathon with four participants, ensuring that no permutations are missed.
What is the difference between permutations and combinations, as hinted in the script?
-While the script does not explicitly define combinations, it implies that the difference lies in the importance of order. Permutations, as discussed, are orderings where the order matters, whereas combinations, which will be discussed later, are groupings where the order does not matter.
How does the script use the word 'cat' to illustrate permutations?
-The script uses the word 'cat' to illustrate that even with just three letters, there are six different permutations possible when the order of the letters is changed, emphasizing that the order matters in permutations.
What is the significance of the notation nPr in the context of permutations?
-The notation nPr represents the number of permutations of n elements taken r at a time. It is a shorthand way of expressing the calculation for permutations without having to list all possible outcomes.
How does the script clarify the use of factorials in calculating permutations?
-The script clarifies the use of factorials by explaining that factorial (e.g., n!) represents the product of all positive integers up to n. It is used in permutation calculations to determine the number of ways events can be ordered.
What is the practical application of permutations in the context of an election with 20 candidates for President, Vice President, and Secretary roles?
-The practical application is to determine the number of different ways the three roles can be filled from the 20 candidates. Using the fundamental counting principle, the script calculates this by multiplying the number of choices for each role (20 for President, 19 for Vice President, and 18 for Secretary), resulting in 6,840 different permutations.
How does the script handle the concept of zero factorial in the context of permutations?
-The script explains that by definition, zero factorial is equal to one, which may seem counterintuitive but is a mathematical convention that simplifies calculations in permutation problems.
What is the difference between nPn and nPr as explained in the script?
-The script explains that nPn, which is the number of permutations of n elements taken n at a time, is equal to n factorial. In contrast, nPr is used when the order of selection matters but not all elements are taken at once, and it is calculated as n factorial divided by (n - r) factorial.
How does the script illustrate the calculation of unique phone numbers in a city where the first three digits are always the same?
-The script illustrates this by focusing on the last four digits of the phone number, which can each be any of the 10 possible digits (0-9). Using the fundamental counting principle, it multiplies the number of choices for each digit (10 x 10 x 10 x 10) to find there are 10,000 unique permutations, or phone numbers.
What is the difference between using the fundamental counting principle and the permutation formula nPr in the script's examples?
-The script explains that both methods are essentially doing the same calculations but are applied in different contexts. The fundamental counting principle is used more generally to calculate permutations by multiplying the number of choices for each event. The permutation formula nPr is a shorthand for this calculation when the problem involves selecting and ordering a subset of elements from a larger set without repetition.
How does the script use the example of radio station call letters to explain permutations?
-The script uses the example of radio station call letters to illustrate permutations where the first letter must be either 'W' or 'K', and the remaining letters can be any of the 26 alphabet letters with repetition allowed. The calculation involves multiplying the number of choices for the first letter (2) by the number of choices for each of the remaining letters (26), resulting in 35,152 permutations.
What is the key takeaway from the script regarding the concept of permutations?
-The key takeaway is that the order of elements matters in permutations. Whether it's arranging letters, choosing race winners, or selecting team members, the order in which elements are arranged results in different permutations. Understanding this is crucial for solving probability and statistics problems involving permutations.
Outlines
📚 Introduction to Probability and Statistics Tutoring
The tutor expresses excitement about teaching probability and statistics, a class often requested by students. The class will start with probability and proceed to statistics, covering a wide range of topics. The tutor acknowledges that many struggle with these subjects due to the abstract nature of word problems, which require interpretation and logical application of concepts, unlike the more mechanical processes of algebra or calculus. Probability involves dealing with uncertain outcomes and likelihoods rather than definite answers, which can be unfamiliar and challenging. The tutor promises a step-by-step approach starting from basic definitions, aiming to demystify these subjects.
🔄 Understanding Permutations and Their Importance
The tutor introduces the concept of permutations, emphasizing their importance in probability and statistics. Using the analogy of a marathon with four runners, the tutor illustrates how permutations involve ordering where the sequence matters. A detailed tree diagram example demonstrates calculating permutations by systematically pairing runners for first and second place, resulting in 12 unique outcomes. The tutor highlights the importance of methodical problem-solving to avoid missing possibilities.
🌱 Fundamental Counting Principle and Permutations
Building on the marathon example, the tutor explains the Fundamental Counting Principle, which is used to calculate the total number of ways a sequence of events can occur. By multiplying the number of ways each event can happen, the tutor shows that there are 12 permutations for the first and second place winners out of four runners. This principle is foundational for understanding permutations and will be applied to more complex problems.
📈 Applying the Fundamental Counting Principle to Permutations
The tutor continues to elaborate on permutations, providing a formal definition and emphasizing that the order of elements is crucial. Using the word 'cat' as an example, the tutor lists all possible letter arrangements, demonstrating the concept of permutations in a simple context. The tutor also introduces the notation nPn, which represents the number of permutations of n elements taken all at once, and explains that it is equivalent to n factorial, reinforcing the relationship between permutations and the Fundamental Counting Principle.
🎯 Calculation of Permutations Using nPr Notation
The tutor introduces the permutation notation nPr, which stands for the number of permutations of n elements taken r at a time. The formula nPr = n! / (n-r)! is explained as a more specific case of the general permutation calculation. The tutor illustrates how this formula simplifies the calculation process for problems where elements are chosen sequentially and cannot be repeated, such as choosing a President, a Vice President, and a Secretary from a group of 20 candidates, resulting in 6,840 permutations.
📘 Permutations in the Context of Phone Numbers and Radio Station Call Letters
The tutor presents two problems involving permutations in different contexts: phone numbers and radio station call letters. For phone numbers with a fixed prefix, the tutor calculates the number of unique numbers possible using the fundamental counting principle, emphasizing that the order of digits matters. For radio station call letters, the tutor explains how to calculate the number of different call signs when the first letter is limited to W or K and letters can be repeated, resulting in 35,152 permutations.
🔢 Permutations of Four-Digit Odd Numbers and Race Finishers
The tutor tackles permutations in the context of four-digit odd numbers greater than 3,000 and the arrangement of race finishers. For the four-digit numbers, the tutor demonstrates how to apply constraints to the selection of each digit and uses the fundamental counting principle to find 3,500 possible permutations. For the race finishers, the tutor explains that the problem fits the permutation formula nPr, calculating 720 ways for 10 people to finish in first, second, and third place.
🖼️ Displaying Paintings and Arranging Letters from 'Dolphin'
The tutor concludes the section with two final permutation problems: arranging paintings and arranging letters from the word 'dolphin.' For the paintings, the tutor calculates the number of ways six paintings can be displayed in six different places using both the fundamental counting principle and the permutation formula, arriving at 720 arrangements. For the 'dolphin' word, the tutor applies the nPr formula to find 210 unique permutations when arranging three non-repeating letters.
Mindmap
Keywords
💡Probability
💡Statistics
💡Word Problem
💡Permutation
💡Combination
💡Fundamental Counting Principle
💡Tree Diagram
💡Factorial
💡nPr
💡Order Matters
💡Race
Highlights
Introduction to a probability and statistics tutor course with a focus on foundational concepts.
Excitement about teaching the class due to long-time requests from students.
The course will start with probability and then move on to statistics.
Common difficulties with probability and statistics due to their abstract nature.
The importance of understanding word problems in probability and statistics.
Distinguishing between permutations and combinations as foundational concepts.
Permutations are orderings where the sequence matters, exemplified by sock arrangements.
Using a marathon race scenario to illustrate permutations and the importance of order.
Introduction to the Fundamental Counting Principle for calculating permutations.
A step-by-step example using a tree diagram to find permutations in a race.
The mathematical formula for permutations of n elements taken r at a time.
Clarification on when to use permutation formulas versus the fundamental counting principle.
Examples of calculating permutations for phone numbers and radio station call letters.
How to determine the number of odd numbers greater than 3,000 that can be formed with repeated digits.
Explanation of how to use the fundamental counting principle for permutations in a race scenario.
The concept of zero factorial being defined as one and its role in permutation calculations.
Final summary emphasizing the importance of order in permutations and the practicality of the fundamental counting principle.
Transcripts
Browse More Related Video

4.4.3 Counting - Permutations and Combinations, and the Permutation Rule

Statistics Lecture 4.7: Fundamental Counting Rule, Permutations and Combinations
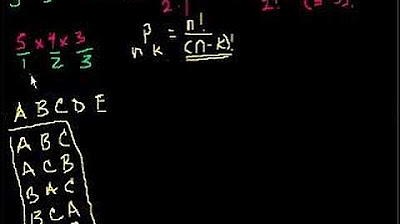
Combinations

4.4.5 Counting - Permutations and Combinations and the Combinations Rule

Permutations, Combinations & Probability (14 Word Problems)

4.4.0 Counting - Lesson Overview, Learning Outcomes, and Key Concepts
5.0 / 5 (0 votes)
Thanks for rating: