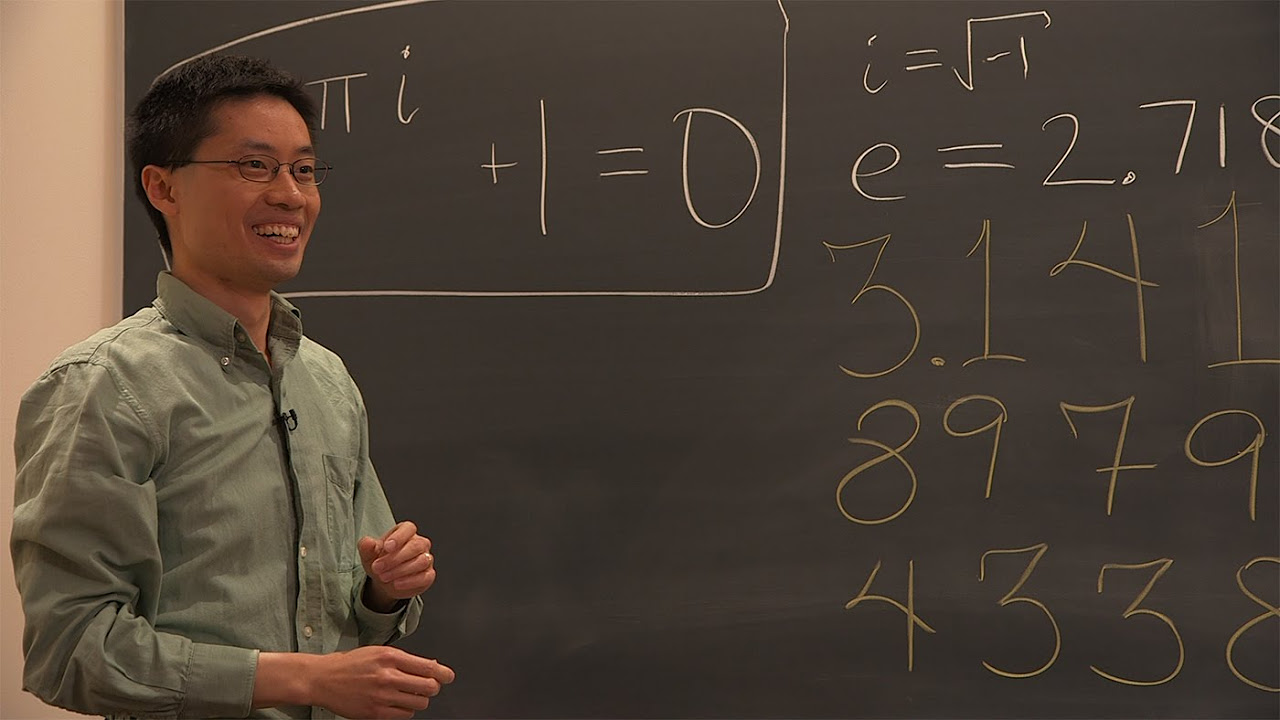Proving the Most Beautiful Equation Bob Ross Style

Tibees

16 Sept 201813:57

EducationalLearning

32 Likes 10 Comments

TLDRIn this engaging video, Toby invites viewers to explore the beauty of mathematics without fear. He begins by introducing Taylor expansions for common functions such as e^x, cosine, and sine, highlighting their similarities and the role of the imaginary unit 'i'. Toby then creatively explains the relationship between these functions and their connection to e^(i*x), which can be expressed as cosine plus i times sine. The video reaches a fascinating climax with Euler's formula, e^(i*pi) = -1, which elegantly combines the constants e, i, and pi into a simple equation. Toby emphasizes the beauty of mathematics through its simplicity and the surprising relationships it reveals. The video also promotes Brilliant.org, offering a platform for deeper mathematical exploration.

Takeaways

📚 Toby introduces Taylor expansions of exponential and trigonometric functions, aiming to demystify their concepts with relatable analogies.
📈 Describes the growth of the exponential function e^x using a personal analogy of increasing love for mathematics, emphasizing its rapid increase.
🌚 Uses creative storytelling to explain the cyclical nature of the cosine function, likening it to life's ups and downs to make the concept more accessible.
🤸 Sine is personified as a character who starts from nothing and experiences cycles of success and failure, illustrating the function's behavior through personal struggle.
📗 Introduces the concept of the imaginary unit i as a helpful 'imaginary friend' in mathematics, specifically in complex calculations.
🤖 Explains the addition of e^ix using i's properties to demonstrate how cosine and sine are related within the complex exponential function.
🎲 Demonstrates how complex numbers and Euler's formula e^iπ = -1 connect e, π, and i, highlighting the beauty and simplicity of this profound equation.
📉 Emphasizes the importance of separating real and imaginary components in complex calculations to avoid confusion, using clear mathematical notations.
📚 Concludes with an application of Euler's formula by replacing x with π, showing how e^iπ + 1 = 0 combines important mathematical constants in a simple yet significant identity.
📢 Mentions the sponsorship and educational opportunities through Brilliant.org, encouraging further exploration of mathematics in a structured online learning environment.

Q & A

What is the main purpose of the video?
-The main purpose of the video is to explore the beauty of mathematics by working through Taylor expansions of common functions and demonstrating the relationship between exponential, trigonometric, and imaginary numbers.
How does the presenter describe the exponential function e^x?
-The presenter describes the exponential function e^x as a function that grows at an alarming rate, increasing with an ever-increasing rate, and uses its shape to metaphorically represent his love for mathematics.
What is the significance of the imaginary unit 'i' in the context of the video?
-The imaginary unit 'i' is used to rewrite the exponential function e^x as e^(i*x), which allows for the exploration of the relationship between exponential and trigonometric functions.
How is the cosine function described in the video?
-The cosine function is described as starting high, experiencing a dip, and then improving, symbolizing the ups and downs of life as a constant cycle.
What is the relationship between the sine and cosine functions in terms of their Taylor series expansions?
-The sine and cosine functions are related in that they both have terms with X to the power of N over N factorial, but cosine uses even powers of X while sine uses odd powers.
What does the presenter do with the function e^(i*x)?
-The presenter manipulates the function e^(i*x) by substituting powers of i, which results in a series of real and imaginary terms that can be separated and identified as cosine and sine functions.
How does the video demonstrate Euler's formula?
-The video demonstrates Euler's formula by showing that e^(i*x) can be rewritten as cosine of x plus i times sine of x, which is a profound relationship between exponential and trigonometric functions.
What is the value of cosine at pi (cos(pi)) according to the video?
-According to the video, the value of cosine at pi is -1, which corresponds to the lowest point in the cosine function's cycle.
What is the value of sine at pi (sin(pi))?
-The value of sine at pi is 0, which is at the midpoint of the sine function's cycle.
What remarkable equation does the presenter derive by substituting pi for x in e^(i*x)?
-The presenter derives the equation e^(i*pi) = -1, which is remarkable because it brings together the constants pi, e, and i, along with the number -1.
What does the presenter suggest about the beauty of mathematical equations?
-The presenter suggests that the beauty of mathematical equations lies in their simplicity and the surprising relationships they reveal between seemingly unrelated mathematical constants or variables.
How does the video relate to the sponsor, Brilliant.org?
-The video relates to Brilliant.org by mentioning that the platform offers online courses in mathematics and other subjects, and by providing a link for viewers to sign up for free and receive a discount on a premium subscription.

Outlines

00:00

📚 Introduction to the Joy of Mathematics

Toby, the host, invites viewers to join him in exploring the beauty of mathematics. He encourages viewers to grab a notepad and pen to follow along and reassures them not to be afraid of mathematics, emphasizing its fun side. He introduces Taylor expansions for common functions like e^x, cos(x), and sin(x), and explains the exponential growth of e^x, comparing it to his love for mathematics. Toby also personifies the trigonometric functions, describing their cyclical nature and how they represent life's ups and downs.

05:03

🔍 Exploring the Relationship Between Functions

The video delves into the similarities between the functions e^x, cos(x), and sin(x), highlighting the common term X^N/N! and how they relate to the functions' respective even and odd terms. Toby introduces the imaginary unit 'i' and uses it to rewrite e^x as e^(i*x), demonstrating how the powers of 'i' cycle through i, -1, -i, and 1. By substituting these values, he separates the real and imaginary components of e^(i*x), revealing that e^(i*x) can be expressed as cos(x) + i*sin(x), thus showcasing a deep connection between these mathematical functions.

10:08

🎓 Euler's Formula and the Beauty of Mathematics

Toby incorporates another fundamental mathematical constant, Pi, into the discussion, explaining its relation to circles and its infinite, non-repeating decimal nature. He then substitutes Pi for x in the equation e^(i*x), resulting in e^(i*Pi). Using the periodic properties of cosine and sine, he determines that cos(Pi) equals -1 and sin(Pi) equals 0, leading to the remarkable equation e^(i*Pi) = -1. This equation is celebrated for its simplicity and the way it unifies three distinct mathematical constants: e, i, and Pi, into a single, elegant expression. The video concludes with a nod to the beauty of such equations and encourages viewers to explore further through online courses on Brilliant.org, with a special offer for the channel's audience.

Mindmap

Keywords

💡Taylor expansions

Taylor expansions are mathematical expressions that represent functions as an infinite sum of terms calculated from the values of the function's derivatives at a single point. In the video, they are used to express common functions such as e^x, cos(x), and sin(x), which are essential for illustrating the relationship between these functions and their underlying mathematical structures.

💡Exponential function (e^x)

The exponential function e^x refers to the function where the base is the mathematical constant e, approximately equal to 2.71828. It is characterized by its rapid growth and is fundamental in various fields such as calculus, exponential growth and decay, and complex numbers. In the video, e^x is used to demonstrate how it can be represented through a Taylor series and its connection to other mathematical functions.

💡Trigonometric functions

Trigonometric functions, specifically cosine and sine, are functions of an angle in a right-angled triangle and are widely used in mathematics to model periodic phenomena. In the video, the presenter uses cosine and sine to show their cyclical nature and how they can be represented through Taylor series expansions, which leads to the exploration of their relationship with the exponential function e^x.

💡Imaginary unit (i)

The imaginary unit i is a mathematical concept where i^2 equals -1. It is a fundamental element in complex numbers, which extend the idea of real numbers to include numbers that cannot be expressed as real numbers alone. In the video, the imaginary unit i is introduced to help rewrite the exponential function e^x as e^(i*x), which is crucial for deriving the relationship between trigonometric functions and the exponential function.

💡Euler's formula

Euler's formula is a profound mathematical equation that states that e^(i*x) = cos(x) + i*sin(x). It is a unifying equation that connects five of the most important numbers in mathematics: e, i, pi, 1, and 0. In the video, the presenter derives Euler's formula to show the deep relationship between exponential, trigonometric, and complex numbers, and to demonstrate the beauty of mathematical simplicity.

💡Pi (π)

Pi, denoted as π, is the ratio of a circle's circumference to its diameter and is an irrational number approximately equal to 3.14159. It is a fundamental constant in mathematics and appears in various formulas related to circles, geometry, and trigonometry. In the video, the presenter replaces x with π in Euler's formula to derive the equation e^(iπ) + 1 = 0, which is a remarkable identity that ties together several mathematical constants.

💡Factorial

A factorial, denoted by n!, is the product of all positive integers less than or equal to n. It is often used in combinatorics and in the definition of the gamma function for complex numbers. In the video, factorials are used in the denominator of terms in the Taylor series expansions for e^x, cos(x), and sin(x), illustrating their importance in defining the coefficients of these series.

💡Complex numbers

Complex numbers are numbers that consist of a real part and an imaginary part, typically written in the form a + bi, where a and b are real numbers, and i is the imaginary unit. They extend the concept of the one-dimensional number line to a two-dimensional complex plane. In the video, complex numbers are used to express the exponential function e^(i*x) and to derive the relationship between trigonometric functions and the exponential function.

💡Cosine and Sine Graphs

The graphs of the cosine and sine functions are periodic waves that represent the ratio of the sides of a right-angled triangle as a function of an angle. They are used to model oscillations and waves in physics and engineering. In the video, the presenter describes the behavior of these graphs to illustrate the cyclical nature of life's ups and downs and to show how they relate to the exponential function through Euler's formula.

💡Euler's Identity

Euler's Identity is a specific case of Euler's formula where x is replaced by π. It is the equation e^(iπ) + 1 = 0, which is often celebrated for its mathematical beauty as it involves the five most fundamental constants of mathematics: e, i, π, 1, and 0. In the video, the presenter derives this identity to highlight the interconnectedness of different areas of mathematics and to demonstrate the elegance of mathematical relationships.

💡Brilliant.org

Brilliant.org is an online platform that offers courses and problem-solving activities in various fields of science, technology, engineering, and mathematics (STEM). In the video, it is mentioned as a sponsor and is recommended for those who wish to delve deeper into mathematics. The presenter provides a link for viewers to sign up for free and offers a discount for an annual premium subscription.

Highlights

Introduction to a session on the joy of mathematics with an invitation for viewers to participate actively.

Explanation of initial fear around mathematics and reassurance about its approachable nature.

Introduction to Taylor expansions for common functions: e^x, cos(x), and sin(x).

Engaging analogy comparing the growth of e^x to an ever-increasing personal love for mathematics.

Creative description of cosine as a cycle of highs and lows, reflecting life's ups and downs.

Personification of sine function as a character who starts from nothing, achieves greatness, then experiences decline.

Introduction of complex numbers with 'i', the imaginary unit, to solve more complex mathematical problems.

Transformation of the exponential function e^x into e^(i*x) using the imaginary unit.

Decomposition of e^(i*x) into real and imaginary parts, connecting it to cosine and sine.

Real-world application and deeper understanding of Euler's formula through engaging teaching methods.

Inclusion of pi into the Euler's formula, leading to a surprising and simple equation e^(i*pi) = -1.

Discussion on the beauty and simplicity of the equation e^(i*pi) = -1, tying together fundamental constants in mathematics.

Encouragement to explore further mathematical concepts through an educational platform, with a special offer.

Invitation to subscribe to the channel for more insightful mathematics lessons.

Personal sign-off wishing viewers an 'absolutely mathematical day', emphasizing the joy and beauty of mathematics.

Transcripts

Browse More Related Video

Euler's formula & Euler's identity | Series | AP Calculus BC | Khan Academy

Polynomial approximation of functions (part 7)

The Most Beautiful Equation in Math

Indefinite Integration (part 7)

Polynomial approximation of functions (part 6)

Imaginary Numbers Explained Bob Ross Style

Proving the Most Beautiful Equation Bob Ross Style

Takeaways

Q & A

What is the main purpose of the video?

How does the presenter describe the exponential function e^x?

What is the significance of the imaginary unit 'i' in the context of the video?

How is the cosine function described in the video?

What is the relationship between the sine and cosine functions in terms of their Taylor series expansions?

What does the presenter do with the function e^(i*x)?

How does the video demonstrate Euler's formula?

What is the value of cosine at pi (cos(pi)) according to the video?

What is the value of sine at pi (sin(pi))?

What remarkable equation does the presenter derive by substituting pi for x in e^(i*x)?

What does the presenter suggest about the beauty of mathematical equations?

How does the video relate to the sponsor, Brilliant.org?