Work, Energy, & Power - Formulas and Equations - College Physics

The Organic Chemistry Tutor
10 Oct 202310:14
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive overview of the fundamental concepts of work, energy, and power. It explains how to calculate work done by a force using various methods, including the dot product formula and the work-energy theorem, which equates work to the change in kinetic energy. The script also delves into the work done by conservative forces and the concept of power as the rate of energy transfer, highlighting the distinction between energy as a possession and work as a transfer of energy. It concludes with the importance of understanding units like watts, kilowatts, and kilowatt-hours, emphasizing the difference between power and energy.

Takeaways
  • πŸ”§ The basic formula for calculating work done by a force is force multiplied by displacement (F * D).
  • πŸ“ When the force and displacement vectors are at an angle, work is calculated using the formula F * D * cos(Theta).
  • πŸ“Š Work can also be found using the dot product of force and displacement vectors, by summing the products of their respective components.
  • πŸš€ The work-energy theorem states that the work done by the net force on an object is equal to the change in its kinetic energy.
  • 🌟 Kinetic energy is given by the formula 1/2 * m * v^2, where m is mass and v is velocity.
  • ⚑ Work done by conservative forces like gravity or a spring is equal to the negative change in potential energy.
  • πŸ“‰ Gravitational potential energy is calculated as m * g * y, and elastic potential energy in a spring is 1/2 * k * x^2.
  • πŸ’¨ The work done by a gas expanding against a piston is negative pressure times the change in volume.
  • ⏱ Power is the rate at which work is done, or energy is transferred, and is measured in watts (Joules per second).
  • πŸ’‘ Energy is a state of an object, like having money in a bank, while work is the transaction, transferring energy from one place to another.
  • ⏫ Power can be calculated as work over time, or alternatively, as force times velocity for both average and instantaneous cases.
  • πŸ”„ Understanding the difference between units of power (watts, kilowatts) and units of energy (joules, kilowatt-hours) is crucial for proper calculations.
Q & A

  • What is the basic formula to calculate work done on an object?

    -The basic formula to calculate work done on an object is the force multiplied by the displacement of the object (W = F * D).

  • How is work done calculated when the force and displacement vectors are perpendicular to each other?

    -When the force and displacement vectors are perpendicular, the work done is zero because the cosine of 90 degrees is zero (W = F * D * cos(90Β°) = 0).

  • What is the work-energy theorem and how is it related to work done?

    -The work-energy theorem states that the work done by the net force acting on an object is equal to the change in the kinetic energy of that object (W_net = Ξ”KE = 0.5 * m * (v_final^2 - v_initial^2)).

  • How do you calculate the work done by a force when you know the components of the force and displacement vectors?

    -You calculate the work done by taking the dot product of the force and displacement vectors, which involves multiplying their respective components and summing the results (W = Fx * Dx + Fy * Dy).

  • What is the formula for kinetic energy and how does it relate to work done?

    -The formula for kinetic energy is KE = 0.5 * m * v^2. The work done by a net force on an object is equal to the change in the object's kinetic energy.

  • How is gravitational potential energy defined and how does it relate to work done by gravity?

    -Gravitational potential energy is defined as m * g * y (or m * g * h). The work done by gravity is equal to negative times the change in gravitational potential energy (W_gravity = -Ξ”PE_gravitational).

  • What is the formula for elastic potential energy stored in a spring and how does it relate to work done by the spring?

    -The formula for elastic potential energy in a spring is PE_elastic = 0.5 * k * x^2. The work done by the spring is equal to the change in elastic potential energy (W_spring = Ξ”PE_elastic).

  • How is work done by a gas expanding against a piston calculated?

    -The work done by a gas expanding is calculated as negative times the pressure times the change in volume of the gas (W_gas = -P * Ξ”V).

  • What is the definition of power and how is it different from work?

    -Power is defined as work divided by time. It is the rate at which energy is transferred, whereas work is the amount of energy transferred by the action of a force on an object.

  • How can you calculate instantaneous power when you have the force and velocity vectors?

    -Instantaneous power can be calculated as the dot product of the force and velocity vectors (P = F * V), where this multiplication gives the component of force in the direction of velocity.

  • What are the standard units for measuring energy, time, and power, and how do they relate to each other?

    -The standard unit for energy is the joule, for time it is the second, and for power it is the watt. One watt represents one joule of energy transferred per second.

  • What is the difference between kilowatts and kilowatt-hours, and how do they relate to power and energy?

    -Kilowatts is a unit of power (1 kilowatt = 1000 watts), while kilowatt-hours is a unit of energy, representing the amount of energy used when a 1-kilowatt device runs for one hour.

Outlines
00:00
πŸ”§ Calculating Work Done by a Force

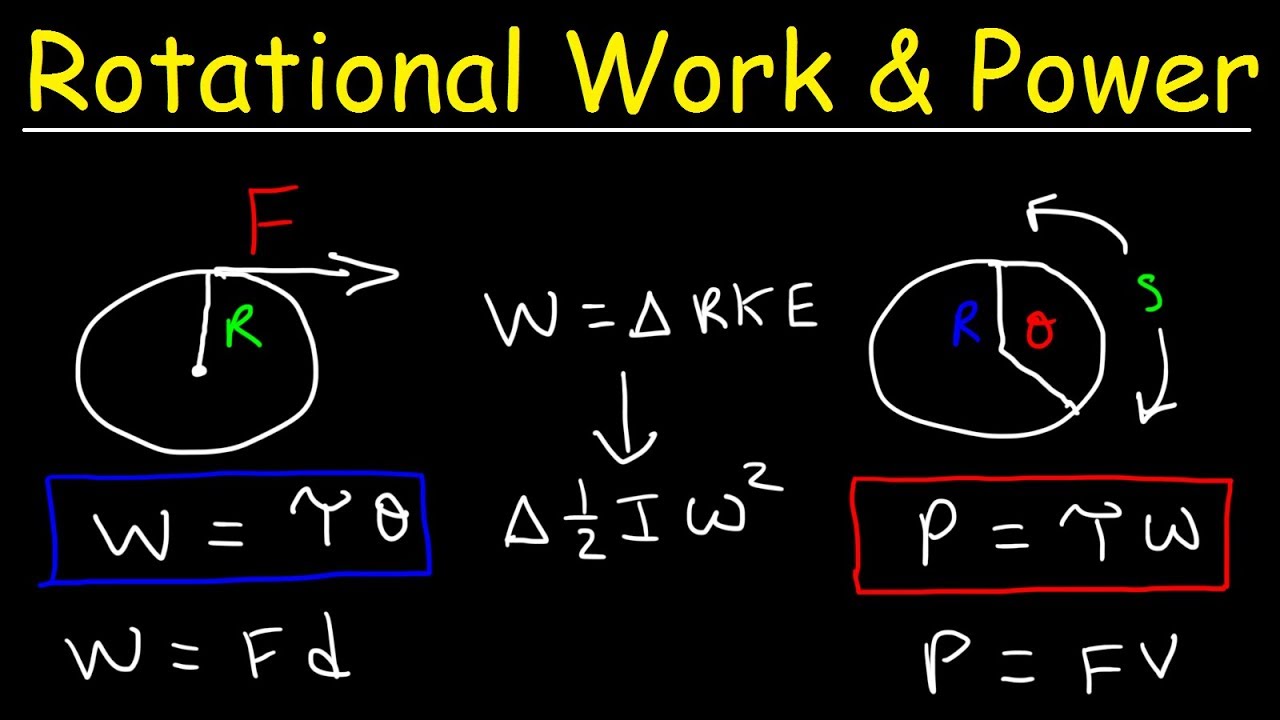
This paragraph discusses the fundamental equations and formulas related to work, energy, and power. It begins with the basic definition of work as the product of force and displacement (W = F Γ— D) when a block moves on a horizontal frictionless surface. It then introduces the concept of work done when there is an angle between the force and displacement vectors, using the formula W = F Γ— D Γ— cos(Θ). The paragraph also covers the calculation of work using vector components and the work-energy theorem, which states that the work done by the net force on an object is equal to the change in its kinetic energy (W = Ξ”KE = 1/2 m(v_final^2 - v_initial^2)). Additionally, it explains how work done by conservative forces like gravity and spring force is related to the change in potential energy.

05:00
⏱ Understanding Power and Its Calculation

The second paragraph delves into the concept of power, defined as the rate at which work is done or energy is transferred over time (P = W/t). It emphasizes the distinction between energy, which an object possesses, and work, which is the transfer of energy. Power is portrayed as the 'transaction' of energy, with watts (W) being the standard unit, representing one joule of energy transferred per second. The paragraph also explains the relationship between power, force, and velocity (P = F Γ— v), and how instantaneous power can be calculated using the dot product of force and velocity vectors. It concludes with a discussion on different units of power, including kilowatts and horsepower, and the difference between power (watts) and energy (joules or kilowatt-hours), highlighting the importance of understanding these units when analyzing energy consumption or production.

10:01
πŸ”„ Clarification on Energy Units and Power

The final paragraph provides a brief clarification on the difference between units of energy and power. It emphasizes that while watts (W) and kilowatts (kW) are units of power, indicating the rate of energy transfer, kilowatt-hours (kWh) is a unit of energy, representing the total energy used over time. This distinction is crucial for understanding energy consumption, as seen on electric bills, where kilowatt-hours are used to measure the total energy consumed during a billing period.

Mindmap
Keywords
πŸ’‘Work
Work in physics is defined as the transfer of energy by a force acting upon an object that moves in the direction of the force. It is central to the video's theme as it discusses how work is calculated and its relationship with energy. For example, the script mentions that 'the work done on the block by the force is going to be equal to the force multiplied by the displacement of the block.'
πŸ’‘Displacement
Displacement refers to the change in position of an object, which is a vector quantity that has both magnitude and direction. It is key in calculating work, as the script explains that 'the work done by a force' is calculated by 'force multiplied by the displacement of the block.'
πŸ’‘Force
Force is any interaction that, when unopposed, will change the motion of an object. It is essential in the context of work, as the video explains that 'work done on the block by the force' is a fundamental concept. The script also discusses calculating work with 'a tension force' and 'the force vector.'
πŸ’‘Dot Product
The dot product is a mathematical operation that takes two vectors and returns a scalar. It is used in the script to calculate work done by a force when the angle between the force and displacement vectors is known, as in 'FD cosine, Theta'.
πŸ’‘Kinetic Energy
Kinetic energy is the energy that an object possesses due to its motion, defined by the formula \( \frac{1}{2}mv^2 \). The video explains that work is also equal to the change in kinetic energy, as stated in 'the work done by the net force acting on an object is equal to the change in the kinetic energy of that object.'
πŸ’‘Work-Energy Theorem
The work-energy theorem links the work done by all forces acting on a system to the change in the system's kinetic energy. The script refers to this theorem when stating that 'work is also equal to the change in kinetic energy' and provides the formula for calculating it.
πŸ’‘Potential Energy
Potential energy is the stored energy of an object based on its position relative to other objects. The video discusses different forms of potential energy, such as gravitational potential energy (mgy or MGH) and elastic potential energy (\( \frac{1}{2}kx^2 \)) and their relation to work done by conservative forces.
πŸ’‘Conservative Forces
Conservative forces are forces for which the work done in moving a particle between two points is independent of the path taken. The script mentions gravity, electric force, and spring force as examples, and explains that 'the work done by conservative forces like Gravity... is equal to negative of the change of the potential energy of the object.'
πŸ’‘Power
Power is the rate at which work is done or energy is transferred, measured in watts. The script emphasizes the difference between power and energy, stating that 'power is work divided by time' and explaining its significance in the context of energy transfer rates.
πŸ’‘Kilowatt and Horsepower
Kilowatt is a unit of power equal to 1,000 watts, and horsepower is a unit of power equivalent to 746 watts. The script uses these units to illustrate different scales of power, helping to contextualize the magnitude of power in various applications.
πŸ’‘Kilowatt-Hour
A kilowatt-hour is a unit of energy, not power. The script clarifies this distinction by explaining that 'the kilowatt hour is not the unit of power, but it is the unit of energy,' which is often used to measure electricity consumption, such as on an electric bill.
Highlights

Work done on a block by a force is calculated as force multiplied by displacement.

Work can also be calculated using the formula FD cosine Theta for a tension force.

If the angle is unknown, work can be found using the dot product of force and displacement vectors.

Work is equal to the change in kinetic energy, as per the work-energy theorem.

Kinetic energy formula is given as 1/2 mv^2.

Work done by conservative forces is the negative change in potential energy.

Gravitational potential energy is calculated as mgy or MGH.

Elastic potential energy in a spring is 1/2 kx^2.

Work done by gravity equals negative change in gravitational potential energy.

Work done by a spring is 1/2 k times the square of the change in position.

Work done by a gas is negative pressure times change in volume.

Power is defined as work divided by time, indicating the rate of energy transfer.

Energy is an object's capacity to do work, while work is the transfer of energy.

Power can be calculated as force times velocity.

Instantaneous power is the dot product of force and velocity vectors.

Units of power include watts, kilowatts, and horsepower.

Kilowatt hour is a unit of energy, not power, representing energy used over time.

Power multiplied by time gives work or change in energy, measured in joules or kilowatt hours.

Transcripts

Browse More Related Video

AP Physics C: Work, Energy, and Power Review (Mechanics)

Rotational Power, Work, Energy, Torque & Moment of Inertia - Physics Problems

Work, Energy, and Power - Basic Introduction

Work and Energy

Work Energy and Power Full Topic

AP Physics 1 review of Energy and Work | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Work EnergyPower CalculationKinetic EnergyPotential EnergyConservative ForcesMechanical WorkPhysics PrinciplesGas ExpansionEnergy TransferEfficiency Analysis