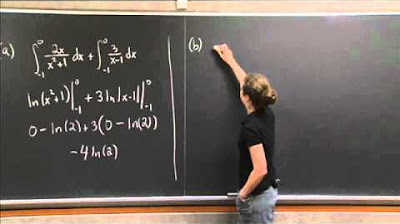the first 5 days of calculus 2 but the integrals get harder!

blackpenredpen

19 Sept 202309:52

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide to various calculus integration techniques over five days. It starts with basic integration, moves on to substitution with an example of integrating x * e to the power of x², and then covers integration by parts. Day four introduces trigonometric identities for integrating square root of 1 + x², and the final day explains partial fraction decomposition. The script also promotes an online learning platform, b.org, for interactive lessons in calculus and other subjects, with a special offer for viewers.

Takeaways

📚 Day One focuses on a basic integration technique where adding one to the integral and dividing by the new power leads to the solution 1/3 * x^3 + C.
🔍 Day Two introduces the substitution method, demonstrating how to integrate x * e^(x^2) by setting u as the inner function and adjusting the integral accordingly to get e^u + C.
📈 Day Three covers integration by parts with the DI format, showing the process of integrating x^2 * e^x and obtaining the result as x^2 * e^x - 2x * e^x + 2 * e^x + C.
🎓 Day Four discusses the 'trick up' method for integrating the square root of 1 + x^2, using trigonometric identities to simplify the expression and resulting in the answer involving secant and tangent functions.
📝 Day Five explains partial fraction decomposition for integrating a rational function, breaking it down into simpler fractions and finding constants a and b to integrate each part.
🧩 The script provides a step-by-step guide for each integration technique, ensuring that viewers can follow along and understand the process.
📉 The use of substitution simplifies the integration of exponential functions by transforming them into a more manageable form.
📐 Integration by parts is shown as a recursive process that can be applied multiple times until a simple integral is reached.
📘 The 'trick up' method cleverly uses trigonometric identities to transform a complex integral into a simpler form involving secant and tangent functions.
🔑 Partial fraction decomposition is a powerful tool for integrating rational functions by breaking them into simpler components that are easier to integrate.
🎁 The video script also promotes an online learning platform, b.org, offering interactive lessons in calculus and other subjects, with a special offer for viewers to try the platform for free.

Q & A

What is the integral of 1/3 x to the 3 power with a constant of integration?
-The integral of 1/3 x to the 3 power is x to the 4th power over 4, plus the constant of integration C.
What is the substitution method used in the script for integrating x * e to the x² power?
-The substitution method sets u to be x², so du = 2x dx, and the integral of x * e to the x² power becomes e to the u with the adjusted dx.
How is the integral of x² * e^x solved using integration by parts?
-Integration by parts is applied by setting D as x² and I as e^x, then differentiating D and integrating I, resulting in x² * e^x - 2x * e^x + 2 * e^x plus C.
What trigonometric identity is used to simplify the integral of the square root of 1 + x²?
-The identity 1 + tan²θ = sec²θ is used to simplify the integral, with x being represented as tanθ.
How is the integral of secant to the third power θ dθ evaluated?
-The integral of secant to the third power θ dθ is evaluated as 1/2 secant θ * tangent θ plus 1/2 ln |secant θ + tangent θ|.
What is partial fraction decomposition and how is it used in the script?
-Partial fraction decomposition is a technique used to break down a complex fraction into simpler fractions that are easier to integrate. In the script, it's used to decompose 2x + 1 / (x - 2)(x - 1) into simpler fractions with constants A and B.
How are the constants A and B in partial fraction decomposition determined?
-Constants A and B are determined by plugging in values of x that make the denominators zero, thus isolating the constants in the numerators.
What is the integral of the decomposed fraction (2x + 1) / (x - 2)(x - 1) after finding constants A and B?
-After finding A = 5 and B = 3, the integral becomes 5 * ln|x - 2| - 3 * ln|x - 1| plus the constant of integration C.
What is the role of the赞助商 (sponsor) in the script and how can viewers benefit from it?
-The赞助商 (sponsor), Khan Academy, is an online learning platform offering interactive lessons in various subjects including calculus. Viewers can benefit from a 30-day free trial and a 20% discount using the provided link.
How does the script emphasize the importance of understanding calculus concepts?
-The script emphasizes the importance of understanding calculus concepts by demonstrating various integration techniques and suggesting interactive learning through the sponsor's platform to enhance comprehension.

Outlines

00:00

📚 Day One: Basic Integration Techniques

The first day of the video script focuses on fundamental integration techniques. The script starts with an integration problem involving the addition of 1 to a function and dividing by a new power, leading to the solution \( \frac{1}{3}x^3 + C \). The second topic of the day is substitution, exemplified by integrating \( x \cdot e^{x^2} \). The process involves setting \( u = x^2 \), differentiating to find \( du = 2x \, dx \), and then integrating \( e^u \) to get \( e^u + C \), which is simplified to \( e^{x^2} + C \) after substituting back. The explanation emphasizes the importance of recognizing the inner function and the steps involved in substitution integration.

05:09

📘 Day Two: Integration by Parts and Trigonometric Identities

The second day introduces integration by parts, using the formula \( \int u \, dv = uv - \int v \, du \). The example given is \( \int x^2 \cdot e^x \, dx \), where \( u = x^2 \) and \( dv = e^x \, dx \), leading to a recursive integration process resulting in \( x^2e^x - 2xe^x + 2e^x + C \). The day also covers the integration of \( \sqrt{1+x^2} \) using trigonometric identities to simplify the expression into a perfect square, which is then integrated to yield \( \frac{1}{2} \sec \theta \tan \theta + \frac{1}{2} \ln | \sec \theta + \tan \theta | + C \). The explanation transitions from trigonometric identities to the actual integration process, emphasizing the simplification of the integral using these identities.

📙 Day Three: Partial Fraction Decomposition

On the third day, the script discusses partial fraction decomposition, a method for integrating rational functions by breaking them down into simpler fractions. The example provided is the integration of \( \frac{2x+1}{(x-2)(x-1)} \), which is decomposed into constants \( A \) and \( B \) over the linear factors \( x-2 \) and \( x-1 \), respectively. Using the cover-up method, the values of \( A \) and \( B \) are determined to be 5 and 3, respectively. The integral is then solved to get \( 5 \ln |x-2| - 3 \ln |x-1| + C \), demonstrating the process of finding constants for partial fractions and integrating the resulting simpler fractions.

🌟 Day Four: Sponsorship and Learning Resources

The fourth and final paragraph of the script is dedicated to a sponsorship message for an online learning platform, b.org, which offers interactive lessons in various subjects, including calculus. The platform is praised for its engaging teaching methods that combine animations and storytelling with mathematical concepts. The script encourages viewers to take advantage of a 30-day free trial and mentions a discount code for additional savings. The sponsorship is acknowledged with gratitude, and the script concludes by thanking the viewers for their interest in calculus and for exploring the recommended learning resource.

Mindmap

Keywords

💡Integration

Integration is a fundamental concept in calculus, referring to the process of finding a function given its derivative. In the video, integration is the main theme, with various techniques demonstrated for solving integrals. For example, the script discusses integrating a function by adding 1 and dividing by a new power, which is a basic integration technique.

💡Substitution

Substitution is a technique used in calculus to simplify the process of integration by replacing a part of the integral with a new variable. The script uses the example of integrating x * e to the power of x², where the substitution of u for the inner function simplifies the integral and makes it easier to solve.

💡Differentiation

Differentiation is the process of finding the derivative of a function, which is a measure of how the function changes as its input changes. In the context of the script, differentiation is used in conjunction with substitution to find the integral of a function, as seen when differentiating both sides of an equation to find du/dx.

💡Integration by Parts

Integration by Parts is a specific method for integrating products of functions. It is analogous to the product rule in differentiation. The script describes using the DI format for integration by parts, where the integral of x² * e^x is solved by differentiating and integrating parts of the function to simplify the integral.

💡Trigonometric Identities

Trigonometric Identities are equations that hold true for various trigonometric functions and are used to simplify complex expressions. In the script, identities like 1 - sin²θ = cos²θ are used to transform the integral of the square root of 1 + x² into a more manageable form, illustrating the use of these identities in integration.

💡Partial Fraction Decomposition

Partial Fraction Decomposition is a technique used to break down a complex rational function into simpler fractions that are easier to integrate. The script explains how to decompose a fraction with a quadratic denominator into two simpler fractions with linear denominators, which can then be integrated using basic integration techniques.

💡Natural Logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational constant approximately equal to 2.71828. In the script, the natural logarithm appears in the context of integrating certain functions, such as when integrating a function that results in ln|x - 2|.

💡Absolute Value

Absolute value of a number refers to its distance from zero on a number line, regardless of direction. It is used in the script when discussing the result of an integral, where the absolute value ensures that the result is non-negative, even though the specific integral in question does not require it due to the nature of the function.

💡Hyperbolic Functions

Hyperbolic functions are analogs of trigonometric functions and are used in various mathematical contexts. Although not explicitly mentioned in the script, the mention of secant squared and tangent squared could imply a connection to hyperbolic functions, as they are used in the context of simplifying the integral of the square root of 1 + x².

💡Online Learning Platform

An online learning platform is a digital environment where students can access educational content and resources. In the script, the platform b.org is mentioned as a place to continue learning calculus with interactive lessons, animations, and storytelling, providing a comprehensive learning experience beyond the video.

💡Sponsor

A sponsor is an individual or organization that provides financial support or endorsement for an event, product, or content. In the script, the learning platform b.org is identified as the sponsor of the video, highlighting the relationship between the content creator and the sponsor in providing educational resources.

Highlights

Day one introduces the concept of integrating a function by adding one and dividing by the new power, resulting in the formula 1/3 * x^3 + C.

Day two discusses the use of substitution in integration, specifically integrating x * e^(x^2) by setting u = x^2 and solving for du.

The integration of e^u is simplified to e^u, demonstrating the power of substitution in simplifying complex integrals.

Day three covers integration by parts, using the DI format to integrate x^2 * e^x, showcasing a method for integrating products of functions.

The process of differentiating and integrating within the DI format leads to a final answer involving e^x terms.

Day four explores the integration of square root of 1 + x^2 using trigonometric identities to simplify the expression.

The use of trigonometric identities such as 1 - sin^2(θ) = cos^2(θ) to simplify the integral is highlighted.

The substitution of x as tangent(θ) to transform the integral into a more manageable form is demonstrated.

The integral of secant^3(θ) dθ is solved and then translated back into terms of x, showcasing the power of substitution with trigonometric functions.

Day five focuses on partial fraction decomposition, a technique for integrating rational functions by breaking them into simpler fractions.

The method of finding constants a and b in partial fraction decomposition using the cover-up method is explained.

The integration of each simplified fraction after decomposition is shown, leading to a natural logarithm and linear terms.

The final answer for the partial fraction decomposition example is presented, including natural logarithms and constants.

The video promotes an online learning platform, b.org, for further learning in calculus with interactive lessons.

The offer of a 30-day free trial on b.org is mentioned, encouraging viewers to explore calculus in an interactive way.

A discount of 20% off is provided for the first-time users of b.org, as part of the sponsorship deal.

Transcripts

Browse More Related Video

Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems

my all-in-one calculus question

Integral of a Product

Calculus 2 - Basic Integration

Indefinite Integral

Integration Practice I | MIT 18.01SC Single Variable Calculus, Fall 2010