This is what a pure mathematics exam looks like at university
TLDRThe video script offers an insightful overview of a pure mathematics exam from a university, highlighting the abstract concepts studied in fields such as real and complex analysis. It emphasizes the difficulty and abstract nature of the subject, which forms the theoretical foundation of mathematics and is applicable in various scientific domains. The script also outlines specific topics covered in the exam, including limits, continuity, the intermediate value theorem, and the Cauchy-Riemann theorem, providing a glimpse into the rigorous and advanced mathematical concepts tackled by undergraduate students in their second or third year.
Takeaways
- 📚 Pure mathematics focuses on abstract concepts, distinct from applied mathematics.
- 🔢 It is beneficial for fields like physics, with the speaker having a double major in math and physics.
- 📝 The exam in question is from the University of Manchester, intended for second or third-year undergraduate students.
- ⏳ The exam consists of eight questions, divided into real and complex analysis, taking three hours to complete.
- 🤔 Students are required to answer five questions, selecting two from real analysis and two from complex analysis, plus one additional question of their choice.
- 🌟 Real analysis involves properties of real numbers and functions, including sequences, convergence, limits, continuity, and smoothness.
- 📈 The first question examines the limit of a function, using techniques like the epsilon-delta definition.
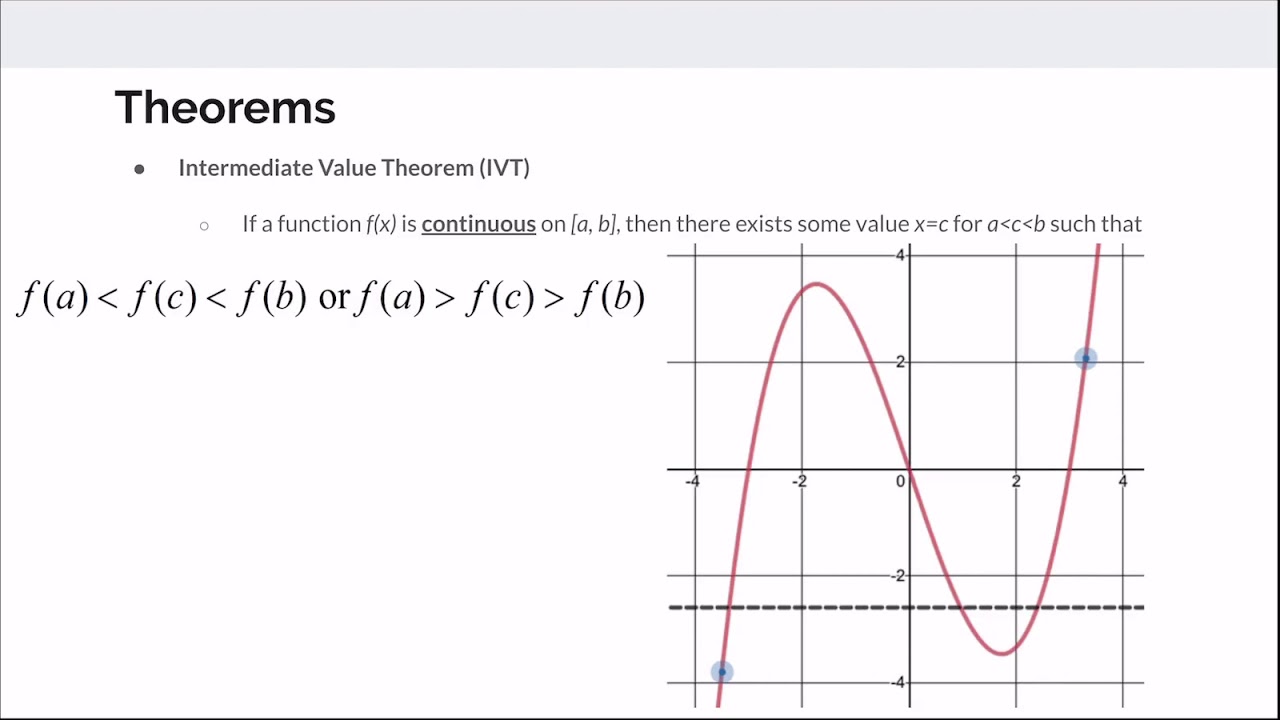
- 🏆 The intermediate value theorem is discussed, which states that a continuous function will cross a given value between two points in its domain.
- 🔄 The product rule for differentiation and the condition for a function's local maximum are explored, requiring proof of the derivative being zero at such points.
- ✨ Complex analysis extends real functions into the complex plane, dealing with functions that can be separated into real and complex parts.
- 🌐 The Cauchy-Riemann theorem is introduced as a test for complex differentiability, also known as holomorphic functions.
- 🔍 The exam also touches on applications of complex analysis in physics, thermodynamics, and fluid mechanics, particularly in the context of integrals.
Q & A
What is the primary focus of pure mathematics?
-Pure mathematics focuses on more abstract concepts rather than applied mathematics. It deals with the theory behind numbers, functions, and other mathematical concepts.
Why is pure mathematics important in education, particularly for those studying physics?
-Pure mathematics is important in education because it provides a strong foundation for understanding the theoretical aspects of other fields, such as physics. It is useful for physics students as it helps them grasp complex concepts and solve problems that require a deep understanding of mathematical principles.
What are the main differences between real analysis and complex analysis?
-Real analysis deals with the properties of real numbers and functions, focusing on concepts like sequences, convergence, limits, continuity, and smoothness. Complex analysis, on the other hand, extends these concepts into the complex plane, dealing with functions that have real and complex parts, and includes topics like the Cauchy-Riemann theorem and holomorphic functions.
How many questions are in the University of Manchester's pure mathematics exam, and how are they structured?
-The exam consists of eight questions, with four dealing with real analysis and four with complex analysis. Students are required to answer five of these questions, selecting two from each section and choosing one additional question of their preference.
What is the significance of the intermediate value theorem in real analysis?
-The intermediate value theorem states that if you have two points connected by a continuous curve, and you have one point below a certain line and another point above that line, then there must be at least one place on the curve where it crosses that line. This theorem is fundamental in understanding the behavior of continuous functions and is a key concept in calculus.
How does the concept of limits play a role in real analysis?
-Limits are central to real analysis as they help describe the behavior of functions as their input approaches a certain value. Understanding limits is crucial for grasping the continuity, differentiability, and other properties of functions.
What is the relationship between a function having a local maximum and its derivative at that point?
-If a function has a local maximum at a certain point, the derivative of the function at that point is 0. This relationship is important in calculus and optimization problems, as it helps identify points of extremal values within a function.
What is the Cauchy-Riemann theorem mentioned in the complex analysis section, and why is it important?
-The Cauchy-Riemann theorem is a set of partial derivative conditions that can be used to test if a function is complex differentiable, or holomorphic. This theorem is crucial in complex analysis as it helps determine the differentiability of functions in the complex plane, which is essential for further analysis and applications.
How do complex analysis applications in physics and other fields differ from those in real analysis?
-Complex analysis extends the concepts of real functions into the complex domain, allowing for the analysis and solution of problems that are not as easily approached with real functions alone. This includes applications in physics, thermodynamics, and fluid mechanics, where complex functions and integrals provide unique insights and solutions that might not be apparent with real analysis alone.
What is the significance of the residue theorem in complex analysis?
-The residue theorem is a powerful tool in complex analysis that allows for the calculation of certain integrals in the complex plane. It simplifies the process of evaluating integrals that would otherwise be difficult or impossible to compute in the real space, making it an essential concept for advanced applications of complex analysis.
Why might students find real analysis more challenging than other mathematics courses?
-Real analysis can be more challenging for students because it introduces a significant amount of new language and abstract concepts. The abstract nature of the subject makes it harder to understand, describe, and apply compared to more concrete mathematical topics.
Outlines
📚 Pure Mathematics Exam Overview
This paragraph introduces a pure mathematics exam from a university, highlighting the abstract nature of the subject. It contrasts pure mathematics with applied mathematics and explains the relevance of pure mathematics to fields like physics. The speaker discusses the structure of the exam, which includes eight questions divided into real and complex analysis, with candidates required to answer five in total. The paragraph delves into the specifics of the first section on real analysis, covering topics such as limits, the intermediate value theorem, differentiability, and the product rule for differentiation. The speaker also shares personal insights about the challenges of studying real analysis due to its abstract language and symbols.
🤔 Challenges and Applications in Complex Analysis
The second paragraph shifts focus to complex analysis, which the speaker finds more appealing due to its practical applications in physics, thermodynamics, and fluid mechanics. It discusses the extension of real functions into the complex domain and the use of complex numbers in trigonometric functions. The speaker mentions the Cauchy-Riemann theorem for testing complex differentiability and the definitions of trig functions in the complex plane. The paragraph also highlights the innovative applications of complex analysis in integrals, such as using the residue theorem and Cauchy's theorem to solve difficult integrations. The speaker provides an overview of how complex analysis can transform challenging integrals into solvable problems in the complex domain and then translate the solutions back into the real domain.
Mindmap
Keywords
💡Pure Mathematics
💡Real Analysis
💡Complex Analysis
💡Limit
💡Intermediate Value Theorem
💡Differentiability
💡Product Rule
💡Cauchy-Riemann Theorem
💡Trigonometric Functions
💡Integrals
💡Residue Theorem
Highlights
The discussion focuses on a pure mathematics exam from a university, emphasizing its abstract concepts.
Pure mathematics, though abstract, does have practical applications in various fields.
The speaker's background in physics education includes studying pure mathematics due to its utility.
The exam is designed for second or third-year university undergraduate students, taking three hours to complete.
The exam consists of eight questions, split equally between real and complex analysis.
Complex analysis involves the theory behind functions in the complex plane, incorporating the imaginary unit 'i'.
The University of Manchester makes their exams publicly accessible, exemplifying transparency.
Students are required to answer five out of the eight questions, selecting two from each analysis section and one at their discretion.
Real analysis examines properties of real numbers and functions, focusing on sequences, convergence, and continuity.
The epsilon-delta definition is used to demonstrate the limit of functions in real analysis.
The intermediate value theorem is a key concept in real analysis, asserting the existence of a function value between two points.
A function's local maximum is characterized by a derivative of zero, a principle explored in the exam.
The product rule for differentiation is one of the topics requiring a proof in the exam.
Complex analysis extends real functions into the complex domain, offering new applications in physics and thermodynamics.
The Cauchy-Riemann theorem is a crucial tool in complex analysis for determining the differentiability of functions.
Trigonometric functions in the complex plane are defined differently and are a focus in the exam.
Complex analysis provides innovative methods for calculating integrals, such as using the residue theorem.
The exam showcases the depth and abstract nature of pure mathematics at the university level.
The speaker's personal experience with real analysis found it challenging due to the new language and abstract concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: