Calculus AB Homework 6.3 Fundamental Theorem of Calculus, Part I

This paragraph discusses solving calculus homework problems from unit six, specifically numbers 20 to 34. The focus is on the Fundamental Theorem of Calculus. For problem 20, the integral of \( T^2 - T \) from -1 to 1 is evaluated by finding antiderivatives and applying the bounds, resulting in a final answer of 2/3. The process is checked using a calculator. Problem 21 involves integrating \( \frac{3}{x^2-1} \) from 1 to 2, rewritten as \( 3x^{-2} - 1 \), and evaluated similarly, yielding 1/2. The paragraph also covers checking answers with a calculator and understanding the optional step of storing the integrand in 'y1'.

The second paragraph delves into the integration of complex functions. It starts with integrating \( u - 2 \) over the square root of \( u \) from 1 to 4, simplifying the integrand and applying the power rule to find the antiderivative, which results in 2/3 after evaluation. The paragraph also covers integrating a function from -1 to -2, emphasizing the correct substitution order and sign management, leading to an answer of 2. Problem 24 involves integrating \( 1 + \sin(x) \) from 0 to \( \pi \), using the antiderivative of \( \sin(x) \) as \( -\cos(x) \), and ends with \( \pi + 2 \). Problem 25 integrates a polynomial from 1 to 3, resulting in 38, and the process includes checking the answer with a calculator.

This paragraph explains how to calculate definite integrals using the area under a graph of a function. It discusses breaking down the area into recognizable shapes for problem 26, which involves integrating from -4 to 2, and results in an area of -6.5. Problem 27 calculates the integral from 0 to 3, using half of a rectangle and resulting in 1. Problem 29 uses the Fundamental Theorem of Calculus to find the integral of \( F'(x) \) from -4 to 0, which equals 3. The paragraph also covers the integral of \( F'(x) \) from -1 to 1, resulting in 4, and from 1 to 3, resulting in -4.

The fourth paragraph explores the properties of definite integrals, using given integral values to find new ones. It starts with the integral of \( F + G \) from 2 to 6, which is calculated as 8 using the sum of given integrals. It continues with the integral of \( -f - 3G \) from 2 to 6, resulting in 26, and the integral of \( G \) from 6 to 2, which is 12 due to the reversal of bounds and multiplication by -1. The paragraph also addresses an integral that cannot be determined with the given information due to the lack of a property for division in integrals.

This paragraph continues the application of properties of definite integrals with new given values. It calculates the integral of \( F + 4 \) from -2 to 4 as 18 and the integral of \( 3G + X \) from -2 to 4 as 18. It also discusses the integral of \( \frac{1}{2}F + 3X^2 \) from -2 to 4, resulting in 69, and uses the graph of \( f'(x) \) to answer questions about the integral from 0 to 7, which sums up to 9.

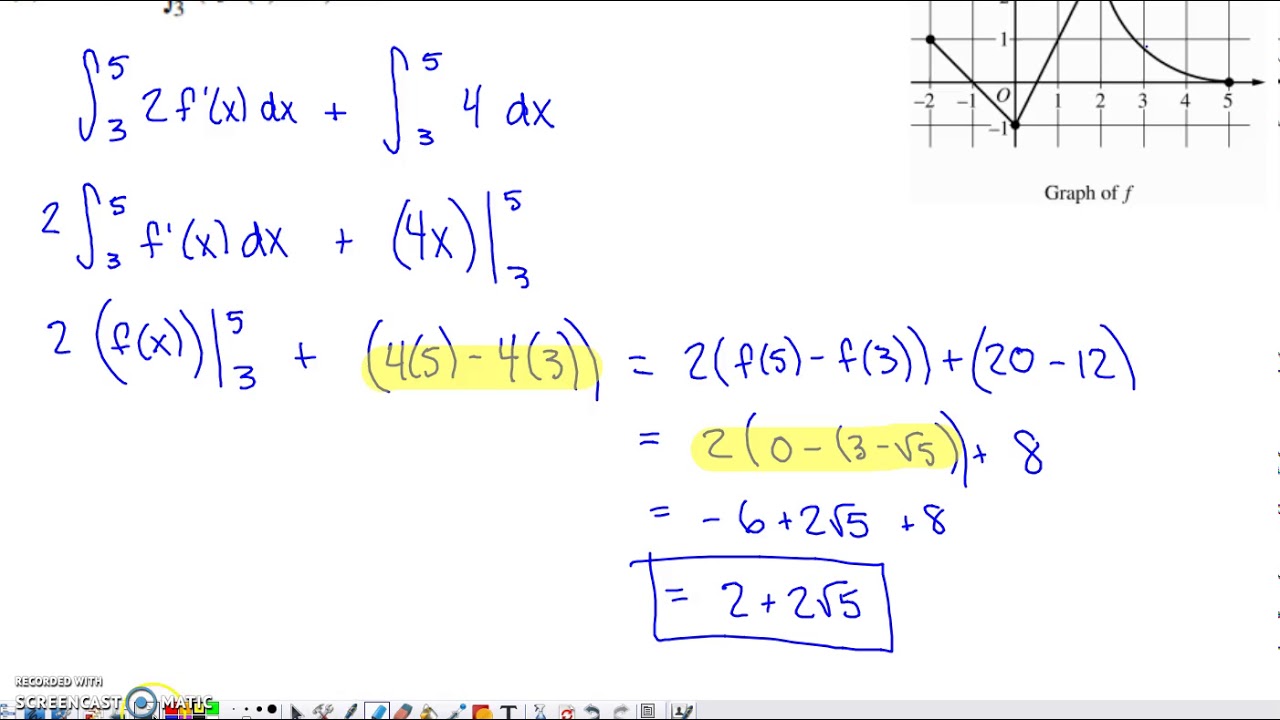
The final paragraph uses the graph of \( f'(x) \) to answer questions about definite integrals and the values of the original function \( f(x) \). It explains how to find \( f(3) \) given \( f(0) \) and the integral of \( f'(x) \) from 0 to 3, resulting in \( f(3) = 0 \). It also finds \( f(7) \) using the integral from 3 to 7, concluding \( f(7) = 5 \). The paragraph emphasizes the relationship between the integral of a derivative and the function values, as per the Fundamental Theorem of Calculus.