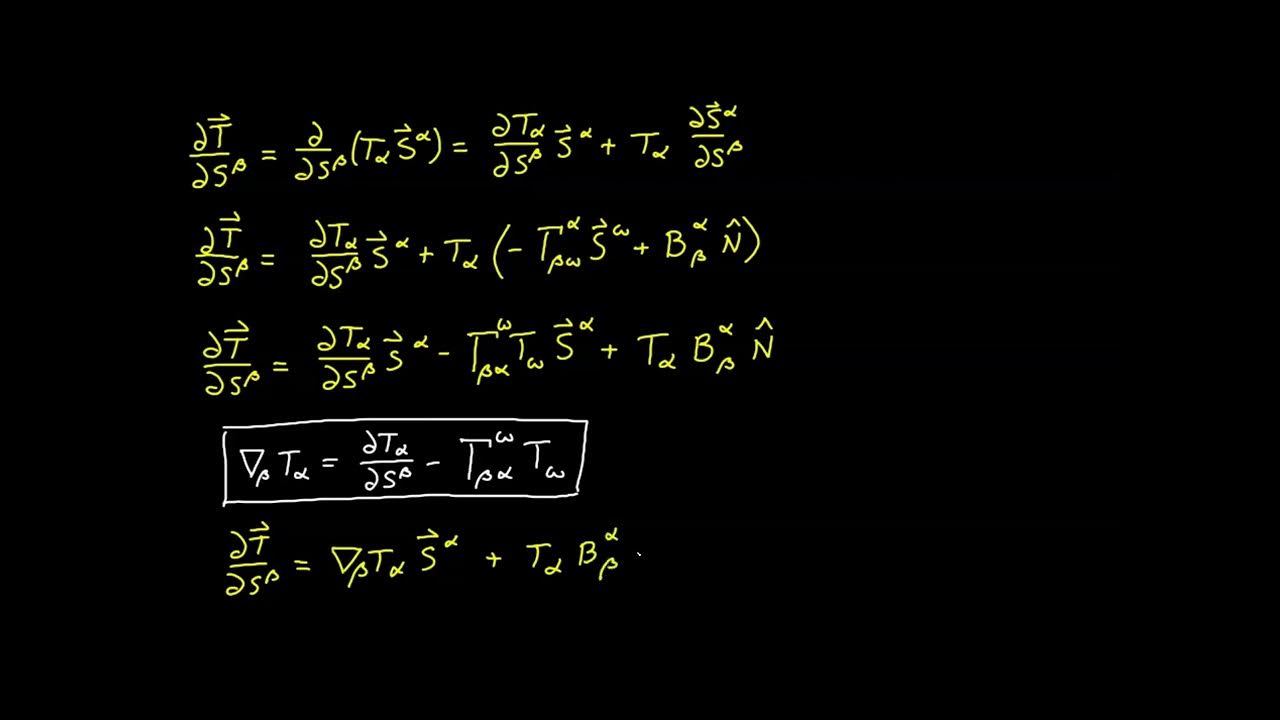Differential Geometry in Under 15 Minutes
TLDRThis script explores the concept of mapping curved surfaces like the Earth onto flat maps while preserving important features and minimizing distortion. It introduces the stereographic projection as a solution and delves into the idea of manifolds, which are spaces that can be covered by open shapes with well-behaved maps. The video also discusses the application of these concepts to analyze functions on manifolds, introduces the tangent plane and vector fields, and explains differential forms and the exterior derivative. It culminates in an explanation of Stokes's theorem, illustrating how these mathematical tools can be applied to both visualize and understand complex geometrical and physical phenomena.
Takeaways
- 🌐 The riddle of traveling north, east, and south a thousand kilometers and ending up at the same location is possible if the starting point is the South Pole, highlighting the importance of considering Earth's spherical shape.
- 🗺 Maps have inherent biases and cannot accurately represent curved surfaces, necessitating mathematical adjustments when working with spherical or curved geometries.
- 📈 The goal of the video is to reconcile the concepts of curved surfaces and flat maps, aiming to create a map that preserves important features and allows for mathematical operations with correction factors.
- 🔍 The stereographic projection is introduced as a method to map a globe onto a flat surface, maintaining the relative distances between points and making mathematical operations less complex.
- 🌍 The concept of manifolds is introduced, defining them as surfaces that can be covered by open shapes with well-behaved maps, applicable to both tangible and abstract objects.
- 🔬 Manifolds can be of any dimension and are not limited to surfaces, allowing for the extension of the concept to abstract objects that are difficult to visualize.
- 📊 The video demonstrates how maps can be helpful in analyzing functions on manifolds by transferring the function to flat space, simplifying the process of determining if a function is smooth.
- 📐 The tangent plane concept is expanded to include abstract manifolds, with tangent vectors defined as functions that measure the rate of change in a specific direction.
- 🌀 Vector fields are assigned to every point on a manifold, varying smoothly, and are used to define concepts like the Lie bracket, which measures the non-commutativity of motion.
- 📚 Differential forms are introduced as a way to measure vector fields, offering an alternative perspective to the directional derivative and allowing for integration on arbitrary manifolds.
- 🌀 The exterior derivative is explained as a way to create new forms from existing ones, relating to concepts like curl and divergence in vector calculus.
- 🧩 Stokes's theorem is presented as a culmination of the concepts discussed, showing how integration of differential forms over areas can be translated to integration over boundaries, generalizing to arbitrary manifolds.
Q & A
What is the riddle presented in the script and what is the solution?
-The riddle is about a man who travels a thousand kilometers north, a thousand kilometers east, a thousand kilometers south, and ends up at the same location. The solution is that this is possible if the man starts at the South Pole and travels along these directions on the Earth's surface, which is a sphere.
What is the main challenge when creating a map for a curved surface like the Earth?
-The main challenge is to preserve the important features of the original curved surface and to create a map that allows for accurate mathematical representation without biases, which can be corrected by applying some correction factor.
Why is the stereographic projection a useful map for a globe?
-The stereographic projection is useful because it creates a unique relationship between each point on the map and each point on the globe, ensuring that points close to each other on the globe remain close on the map, making mathematical operations less awkward.
What is a manifold and what are its defining characteristics?
-A manifold is a surface that can be covered by open shapes, where each shape only contains the space inside it and the outline doesn't count. Each shape must have a nicely behaving map, and manifolds can be of any dimension, not just surfaces.
How can we analyze if a function on a manifold is smooth using maps?
-We can analyze the smoothness of a function on a manifold by looking at the map for the region of interest. By moving each point in flat space to the corresponding point on the manifold through the map and then applying the function, we can determine if the function is smooth in the region covered by the map.
What is a tangent vector and how is it related to the concept of a tangent plane?
-A tangent vector is a function that describes how quickly a certain property, like the height of terrain, changes in the direction of a curve at a specific point in time. It is related to the tangent plane concept as it provides a way to describe the direction and rate of change on a manifold, which can be visualized as a plane touching the surface at a point.
What is a vector field and how does it vary smoothly on a manifold?
-A vector field is an assignment of a tangent vector to every point in the manifold such that they vary smoothly. This means that if the same smooth function is applied to every tangent vector, the output will also be a smooth function.
What is the significance of the Lie bracket in the context of vector fields?
-The Lie bracket measures the difference between the vector fields when one component acts on the other. A non-zero Lie bracket indicates that the order in which we travel in different directions matters, which is a property not present in regular Cartesian coordinate systems.
How does differential geometry help in understanding concepts like curl and divergence?
-Differential geometry allows us to reconcile the concepts of curl and divergence as a single derivative through the use of exterior derivatives and differential forms. This provides a unified framework for understanding these vector calculus concepts in a broader context.
What is Stokes's theorem and how does it relate to integration on manifolds?
-Stokes's theorem states that integrating a two-form (resulting from the exterior derivative of a one-form) over a region is equivalent to integrating a one-form over the boundary of that region. It generalizes to arbitrary manifolds and allows for integration by transforming the manifold into a flat space and adjusting for area differences with the Jacobian.
Outlines
🌐 Understanding Manifolds and Map Projections
This paragraph introduces the concept of a manifold and the challenges of mapping a curved surface like the Earth. It uses the riddle of a man traveling north, east, and south to return to his starting point, which is possible if he starts at the South Pole. The discussion then shifts to the idea of creating maps that can accurately represent a globe on a flat surface, highlighting the limitations of naive approaches like projecting every point onto the equator. The paragraph introduces the stereographic projection as a method to map the globe, which preserves the proximity of points and allows for mathematical operations on a flat surface. It also touches on the concept of manifolds in higher dimensions and abstract objects, emphasizing that manifolds are not limited to surfaces.
📚 Exploring Tangent Vectors and Vector Fields on Manifolds
The second paragraph delves into the visualization of tangent vectors on manifolds and the abstraction of this concept beyond regular surfaces. It explains how tangent vectors can be defined for abstract manifolds using curves and functions that describe the rate of change in a certain direction. The paragraph also introduces vector fields, which assign a tangent vector to every point on the manifold smoothly. It discusses solution curves that follow these tangent vectors and the concept of the Lie bracket, which measures the non-commutativity of motion. The paragraph further explores differential forms as an alternative way to understand vector fields, explaining how they can be used to measure components of a vector field in specific directions. The exterior derivative is introduced as a means to transition from zero forms to one forms and eventually to two forms, relating these mathematical constructs to concepts like curl and divergence in vector calculus.
🧩 Integrating Differential Forms and Stokes's Theorem on Manifolds
The final paragraph discusses the integration of differential forms on arbitrary manifolds and introduces Stokes's theorem in this context. It starts with an analogy of integrating a differential form over a circle and the challenges it presents, then explains how to map this problem to a Cartesian space for easier integration. The paragraph highlights the importance of the Jacobian in adjusting for differences in areas during the transformation. Stokes's theorem is then explained as a way to relate the integration of a two form over a region to the integration of a one form over the boundary of that region. The physical analogy of water flow is used to illustrate how the effects cancel out in neighboring cells, leaving only the flow around the boundary. The paragraph concludes by emphasizing the generalizability of Stokes's theorem to arbitrary manifolds and forms, and it encourages viewers to look beyond the visual representations to understand the rigorous mathematical analysis behind differential geometry.
Mindmap
Keywords
💡Riddle
💡Stereographic Projection
💡Manifold
💡Tangent Plane
💡Vector Field
💡Lie Bracket
💡Differential Forms
💡Exterior Derivative
💡Stokes's Theorem
💡Integration on Manifolds
Highlights
A riddle is presented where a man travels north, east, and south a thousand kilometers each, ending up at the same location, which is possible if starting at the South Pole.
The challenge of representing a curved surface like the Earth on a flat map is discussed, emphasizing the biases and inaccuracies of map projections.
The concept of creating a map that preserves important features of a curved surface and allows for mathematical operations on a flat surface is introduced.
The stereographic projection is explained as a method to map points on a globe to a flat surface, maintaining the proximity of close points.
The north and south poles are addressed as special cases in map projections, with the creation of two maps to cover the entire globe.
The video aims to demonstrate that a sphere is a manifold and explains the technical definition of a manifold.
Manifolds are described as not limited to surfaces, extending to higher dimensions and abstract objects.
The usefulness of maps in analyzing functions on manifolds is discussed, with an example of analyzing the smoothness of a terrain function.
The concept of a tangent plane on a surface and its generalization to abstract manifolds through curves and tangent vectors is introduced.
Vector fields and their assignment of tangent vectors to every point in a manifold are explained, emphasizing smooth variation.
The Lee bracket is introduced as a measure of the non-commutativity of motion in vector fields, contrasting with Cartesian coordinate systems.
Differential forms are presented as an alternative way to measure vector fields, with examples of one-forms and two-forms.
The exterior derivative is explained as a special operator that transforms zero forms into one forms, and its relation to curl and divergence.
Stokes's theorem is discussed as a fundamental result in calculus, relating the integration of differential forms to physical concepts like curl.
Integration on arbitrary manifolds is explored, with an example of integrating over a circle using a mapping to Cartesian space.
The Jacobian is introduced as a factor to adjust for differences in areas when integrating over transformed spaces.
The video concludes by emphasizing the importance of rigorous mathematical analysis to fully appreciate differential geometry, beyond the provided analogies and animations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: