Standard deviation (simply explained)

DATAtab
19 Sept 202107:48
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the concept of standard deviation, explaining its role as a measure of data dispersion around the mean. It illustrates the calculation process through an example involving people's heights, starting with finding the mean and then calculating the deviation of each individual from this mean. The script clarifies the difference between the two formulas for standard deviation—one for a population and another for a sample—and emphasizes using the latter for most practical scenarios. It also distinguishes standard deviation from variance, highlighting that variance is the squared standard deviation and thus more challenging to interpret. The video concludes with a tip on using an online tool, Beta Tab, for calculating standard deviation, making the process accessible and straightforward.

Takeaways
  • 📊 Standard Deviation Explained: The script defines standard deviation as a measure of how much data scatters around the mean.
  • 📈 Calculating the Mean: To find the mean, sum up all individual values and divide by the number of individuals.
  • 📐 Understanding Deviation: Each individual's deviation from the mean is calculated to understand the spread of data.
  • 🔢 Average Deviation: Standard deviation represents the average amount by which individuals deviate from the mean.
  • 📚 Formula for Standard Deviation: The script provides the formula for calculating standard deviation, involving summing squared deviations and taking the square root.
  • 👥 Population vs. Sample: There are two formulas for standard deviation, one for the entire population (dividing by n) and one for a sample (dividing by n-1).
  • 🧐 Practical Application: The script suggests using the sample formula (n-1) unless the data represents the entire population.
  • 🔍 Difference Between Variance and Standard Deviation: Variance is the squared average distance from the mean, while standard deviation is the square root of variance.
  • 📝 Interpretation of Units: Standard deviation is easier to interpret and is always in the same unit as the original data.
  • 🛠️ Online Tool Recommendation: The script recommends using an online tool like Beta Tab on datadept.net for calculating standard deviation.
Q & A

  • What is standard deviation?

    -Standard deviation is a measure of how much your data scatters around the mean. It indicates the average distance of each data point from the mean value.

  • How do you calculate the mean of a data set?

    -To calculate the mean, you sum up all the values in the data set and then divide by the number of values.

  • What does it mean when a person deviates from the mean in the context of standard deviation?

    -When a person deviates from the mean, it means the difference between their value and the average (mean) value of the data set.

  • Why is the standard deviation calculated using the square root of the sum of squared deviations?

    -The square root of the sum of squared deviations is used to find the average distance of the data points from the mean, which gives the standard deviation. Squaring the deviations ensures that all values are positive and emphasizes larger deviations.

  • What is the difference between using n and n-1 in the standard deviation formula?

    -The choice between n and n-1 depends on whether you are calculating the standard deviation for an entire population or estimating it from a sample. n is used for the population, while n-1 is used for a sample to provide an unbiased estimate.

  • Why would the result of using the arithmetic mean for deviations always be zero?

    -Using the arithmetic mean for deviations would always result in zero because positive and negative deviations would cancel each other out, making the sum zero.

  • What is the quadratic mean in the context of standard deviation?

    -The quadratic mean is the square root of the average of the squared values. It is used in the calculation of standard deviation instead of the arithmetic mean to avoid the issue of deviations canceling each other out.

  • How does variance relate to standard deviation?

    -Variance is the squared average distance from the mean, and it is the squared value of the standard deviation. The standard deviation is the square root of the variance.

  • Why is standard deviation preferred over variance when describing a data set?

    -Standard deviation is preferred because it is in the same unit as the original data, making it easier to interpret and understand. Variance, being squared, has units that are the square of the original data, which can be less intuitive.

  • What is the tip provided for calculating standard deviation?

    -The tip provided is to use an online tool like Beta Tab, which can be found at datadept.net. You can copy your data into the table, select the variable, and it will calculate the standard deviation for you.

Outlines
00:00
📊 Understanding Standard Deviation

The first paragraph introduces the concept of standard deviation as a measure of data dispersion around the mean. It explains the process of calculating the mean and then determining how much each data point deviates from this mean. The standard deviation is illustrated through an example involving the heights of individuals, showing how to calculate it using the formula involving the sum of squared deviations divided by the number of observations. The paragraph also touches on the difference between using the arithmetic mean and the quadratic mean in standard deviation calculations, emphasizing the latter's importance to avoid a zero result. Lastly, it mentions the two formulas for standard deviation, one for the entire population (dividing by n) and one for a sample (dividing by n-1), explaining when to use each.

05:02
🔍 Standard Deviation vs Variance and Practical Tips

The second paragraph delves into the distinction between standard deviation and variance. It clarifies that while standard deviation is the average distance of data points from the mean, variance is the squared average distance. The paragraph explains that variance is the square of the standard deviation and vice versa, but the squaring makes variance difficult to interpret because its unit does not match the original data. It recommends using standard deviation for sample description due to its interpretability and unit consistency with the original data. The paragraph concludes with a practical tip for viewers, suggesting an online tool called 'beta tab' on datadept.net for easily calculating standard deviation by inputting data and selecting the variable of interest.

Mindmap
Keywords
💡Standard Deviation
Standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of values. In the context of the video, it is used to describe how much the heights of individuals in a group vary from the average height. The video explains that standard deviation is calculated by taking the square root of the sum of the squared differences between each data point and the mean, divided by the number of observations. This concept is central to understanding data dispersion and is illustrated with an example where the mean height is 155 centimeters and the standard deviation is calculated to be 12.06 centimeters.
💡Mean
The mean, often referred to as the average, is a measure of central tendency that represents the sum of all data points divided by the number of data points. In the video, the mean is calculated by summing the heights of all individuals in the group and dividing by the number of individuals. The mean serves as a reference point from which deviations are measured to calculate the standard deviation, highlighting its importance in statistical analysis.
💡Deviation
Deviation refers to the difference between an individual data point and the mean of the dataset. In the script, the deviation is demonstrated by measuring how much each person's height deviates from the mean height of 155 centimeters. For example, one person might deviate by 18 centimeters, while another by 8 centimeters. These individual deviations are crucial for calculating the standard deviation, which provides insight into the overall spread of the data.
💡Variance
Variance is a statistical measure that indicates the spread of a set of numbers. It is the average of the squared differences from the mean. The video clarifies that variance is related to standard deviation as it is the squared form of the standard deviation. The variance is less commonly used in practice because its unit is squared, making it less intuitive to interpret compared to standard deviation. The script mentions that variance is the squared average distance from the mean, and standard deviation is the square root of variance.
💡Population
In statistics, the term 'population' refers to the entire group that is the subject of a study. The video explains that when calculating the standard deviation for an entire population, the formula involves dividing by the number of individuals in the population (n). For example, if one wanted to know the standard deviation of the height of all American professional soccer players, the population formula would be used.
💡Sample
A sample is a subset of a population that is used to represent and analyze the larger group. The video discusses that when it is not possible to measure the entire population, a sample is taken and used to estimate the standard deviation of the population. The formula used in this case involves dividing by the number of observations in the sample minus one (n-1), which is known as Bessel's correction.
💡Bessel's Correction
Bessel's correction is a statistical adjustment used in the calculation of the sample standard deviation to provide an unbiased estimate of the population standard deviation. The video mentions that when calculating the standard deviation from a sample rather than the entire population, the formula should divide by n-1 instead of n. This adjustment helps to account for the smaller sample size and ensures that the sample standard deviation is not an underestimate of the population standard deviation.
💡Quadratic Mean
The quadratic mean, also known as the root mean square (RMS), is the square root of the average of the squares of the data points. The video script explains that when calculating standard deviation, the quadratic mean is used rather than the arithmetic mean to avoid the result always being zero. This concept is important because it ensures that the standard deviation reflects the actual spread of the data.
💡Data Scatter
Data scatter refers to the dispersion of data points around the mean in a dataset. The video uses the term to describe how the heights of individuals in a group are spread out around the average height. A larger standard deviation indicates a greater degree of scatter, meaning that the data points are more spread out from the mean, while a smaller standard deviation indicates that the data points are closer to the mean.
💡Online Calculation Tools
The video script mentions online tools like Beta Tab as a convenient way to calculate standard deviation. These tools allow users to input their data into a table and select the variable for which they want to calculate the standard deviation. The tool then provides the result, making the process easier and less prone to error, especially for those who may not be comfortable with manual calculations.
Highlights

Standard deviation is a measure of how much data scatters around the mean.

Calculating the mean involves summing heights and dividing by the number of individuals.

Standard deviation indicates how much each person deviates from the mean value.

Average deviation from the mean is what standard deviation measures.

The formula for standard deviation involves summing square deviations and dividing by the number of values.

The standard deviation is calculated as the root of the sum of square deviations divided by the number of people.

Quadratic mean, not arithmetic mean, is used for calculating standard deviation to avoid a zero result.

There are two formulas for standard deviation: one for the whole population (n) and one for a sample (n-1).

Use n for the whole population and n-1 for estimating the population standard deviation from a sample.

The difference between standard deviation and variance is that variance is the squared average distance from the mean.

Variance is the squared standard deviation, and standard deviation is the root of the variance.

Variance is difficult to interpret due to its unit not matching the original data.

Standard deviation is preferred for describing a sample because it's in the same unit as the original data.

Online tools like Beta Tab can be used to calculate standard deviation easily.

Visit datadept.net to use Beta Tab for calculating standard deviation.

The video provides a tip for calculating standard deviation using online resources.

Transcripts

Browse More Related Video

Standard Deviation and Variance

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

Variance and Standard Deviation: Sample and Population Practice Statistics Problems

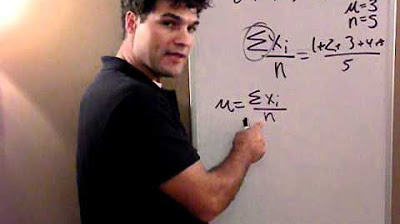
What is a "Standard Deviation?" and where does that formula come from

Find the Mean, Variance, & Standard Deviation of Frequency Grouped Data Table| Step-by-Step Tutorial

Standard Deviation & Degrees of Freedom Explained | Statistics Tutorial | MarinStatsLectures

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Standard DeviationVarianceData AnalysisStatistical MeasureMean ValuePopulation SampleScatter MeasureOnline CalculatorDatadept.netEducational Video