Mixture Problems
TLDRIn this video, we tackle mixture problems using a practical example involving acid solutions. By mixing a 20% acid solution with a 40% acid solution to obtain 20 liters of a 28% acid solution, we determine the required volume of the 20% solution using a weighted average and a specific equation (c1v1 + c2v2 = c3v3). The video also explains the impact of varying solution volumes on the final concentration. Additionally, it covers how to solve similar problems, such as mixing alcohol solutions and diluting solutions with water, highlighting the step-by-step algebraic process to find exact answers.
Takeaways
- 📊 Mixture problems involve combining solutions with different concentrations to achieve a desired final concentration.
- 🔬 Example: Mixing a 20% acid solution with a 40% acid solution to produce 20 liters of a 28% acid solution.
- 📉 The concentration of the mixture will always be between the concentrations of the original solutions.
- 🧪 The total volume of the mixture is the sum of the volumes of the individual solutions.
- 📝 To find the exact amounts of each solution needed, use the equation: c1v1 + c2v2 = c3v3.
- 📐 In the given example, more of the 20% acid solution is needed than the 40% acid solution because the final concentration is closer to 20%.
- 🔢 Use algebra to solve for the unknown volume: c1x + c2(20-x) = c3*20.
- 🧮 Solving the equation for x gives the volume of the 20% acid solution needed.
- 💡 When mixing two solutions with different concentrations, the mixture's concentration is a weighted average.
- 💦 Adding pure water to a solution dilutes it, decreasing its concentration proportionally to the increase in volume.
Q & A
What is the main topic of the video?
-The main topic of the video is solving mixture problems, specifically focusing on how to determine the amounts of different solutions needed to create a mixture with a desired concentration.
What is the initial example problem presented in the video?
-The initial example problem is about a student who mixes a 20% acid solution with a 40% acid solution to produce 20 liters of a 28% acid solution, and the task is to find out how many liters of the 20% acid solution were needed.
Why is the concentration of the mixture less than the average of the two original solutions?
-The concentration of the mixture is less than the average of the two original solutions because the mixture has a weighted average, influenced by the volumes of the solutions being mixed. In the example, more of the 20% solution was used, which pulls the average concentration down.
What equation is used to solve mixture problems as described in the video?
-The equation used to solve mixture problems is c1*v1 + c2*v2 = c3*v3, where c1 and c2 are the concentrations of the first and second solutions, v1 and v2 are their respective volumes, c3 is the concentration of the mixture, and v3 is the volume of the mixture.
How does the volume of the mixture (v3) relate to the volumes of the original solutions (v1 and v2)?
-The volume of the mixture (v3) is the sum of the volumes of the original solutions (v1 and v2). This is because when solutions are mixed, their volumes are additive.
What is the final concentration of the mixture in the initial example after solving the equation?
-The final concentration of the mixture in the initial example is 28% acid, which is the desired concentration stated in the problem.
What is the second problem presented in the video, and what is the expected concentration range of the mixture?
-The second problem involves mixing 50 liters of a 15% alcohol solution with 150 liters of a 35% alcohol solution. The expected concentration range of the mixture is between 25% and 35%, with the weighted average being closer to 35% due to the larger volume of the 35% solution.
How does the volume of the higher concentrated solution affect the final concentration of the mixture?
-The volume of the higher concentrated solution affects the final concentration of the mixture by making the weighted average closer to the concentration of the solution with the larger volume. In the second problem, the mixture's concentration is closer to 35% because there is more volume of the 35% solution.
What happens to the concentration of an alcohol solution when water is added?
-When water, which has zero alcohol content, is added to an alcohol solution, the concentration of the alcohol decreases. This is because the total volume of the solution increases without adding any additional alcohol, thus diluting the solution.
In the third problem, what is the new concentration of the alcohol solution after adding 60 liters of water to 20 liters of a 28% alcohol solution?
-After adding 60 liters of water to 20 liters of a 28% alcohol solution, the new concentration of the alcohol solution is 7%. This is calculated using the mixture equation and considering the increased volume and the dilution effect.
What general principle can be applied when solving mixture problems as demonstrated in the video?
-The general principle applied when solving mixture problems, as demonstrated in the video, is using the equation c1*v1 + c2*v2 = c3*v3 to determine the unknown volumes or concentrations in a mixture, taking into account the additive nature of volumes and the concept of weighted averages.
Outlines
🧪 Solving Mixture Problems with Acid Solutions
The video begins by addressing a mixture problem involving acid solutions. A student mixes a 20% acid solution with a 40% acid solution to create 20 liters of a 28% acid solution. The video explains the concept of concentration and volume when mixing solutions, and introduces an algebraic equation to solve such problems: (c1v1 + c2v2 = c3v3). The goal is to find the volume of the 20% acid solution needed (denoted as x or v1). By setting up the equation with the given concentrations and total volume, the video demonstrates algebraic manipulation to solve for x, revealing that more than 10 liters of the 20% solution is required. The video also poses a similar problem involving alcohol solutions to illustrate the weighted average concept and the use of the equation in solving mixture problems.
🍷 Calculating the Concentration of Alcohol Mixture
This paragraph delves into another mixture problem, this time involving alcohol solutions. The task is to find the concentration of a mixture formed by combining 50 liters of a 15% alcohol solution with 150 liters of a 35% alcohol solution. The video explains the concept of a weighted average, emphasizing that the larger volume of the 35% solution will influence the final concentration more significantly. Using the formula (c1v1 + c2v2 = c3(v1 + v2)), the video calculates the exact concentration of the mixture, which turns out to be 30%. This result is consistent with the expectation that the concentration should be between the average of 15% and 35% but closer to the higher concentration due to the larger volume of the 35% solution.
💧 Determining the Effect of Dilution on Alcohol Concentration
The final paragraph of the script discusses the effect of dilution on the concentration of an alcohol solution. A student adds 60 liters of water to 20 liters of a 28% alcohol solution, and the video aims to find the new concentration of the alcohol solution. By applying the same formula used earlier but considering the concentration of water as 0% alcohol, the video calculates the new concentration after dilution. The video explains that adding water decreases the concentration of the alcohol and uses the formula to show that the new concentration is 7%. This illustrates the principle that diluting a solution with water reduces its concentration, and the video concludes by emphasizing the usefulness of the formula in solving mixture problems.
Mindmap
Keywords
💡Mixture Problems
💡Concentration
💡Acid Solution
💡Volume
💡Weighted Average
💡Algebraic Equation
💡Dilution
💡Alcohol Solution
💡Percentage
💡Solution
Highlights
The video focuses on solving mixture problems involving acid solutions.
A student mixes a 20% acid solution with a 40% acid solution to create a 28% acid solution.
The total volume of the mixture is 20 liters.
An equal mix of 10 liters of each solution would result in an average concentration of 30%, but the actual mixture is 28%.
The mixture's concentration is less than the average of the two original solutions, indicating an unequal mix.
More of the 20% acid solution is mixed than the 40% acid solution.
An equation c1v1 + c2v2 = c3v3 is introduced to solve mixture problems.
The volume of the mixture (v3) is the sum of the volumes of the original solutions (v1 + v2).
The goal is to find the volume (v1) of the 20% acid solution needed.
Algebra is used to solve for x, representing the volume of the 20% acid solution.
The exact amount of the 20% acid solution required is more than 10 liters.
The volume of the 40% acid solution needed is less than 10 liters.
The final answer for the volume of the 20% solution is 12 liters.
A second problem involves mixing a 15% alcohol solution with a 35% alcohol solution.
The concentration of the mixture is found to be 30%, influenced by the higher volume of the 35% solution.
Adding water to an alcohol solution decreases its concentration.
The new concentration of the alcohol solution after adding water is calculated to be 7%.
The video concludes with the recommendation to use the provided equation for solving similar mixture problems.
Transcripts
Browse More Related Video

How many oz of 5% acid and 20% acid must be mixed to get 10 oz of a solution that is 12.5% acid?
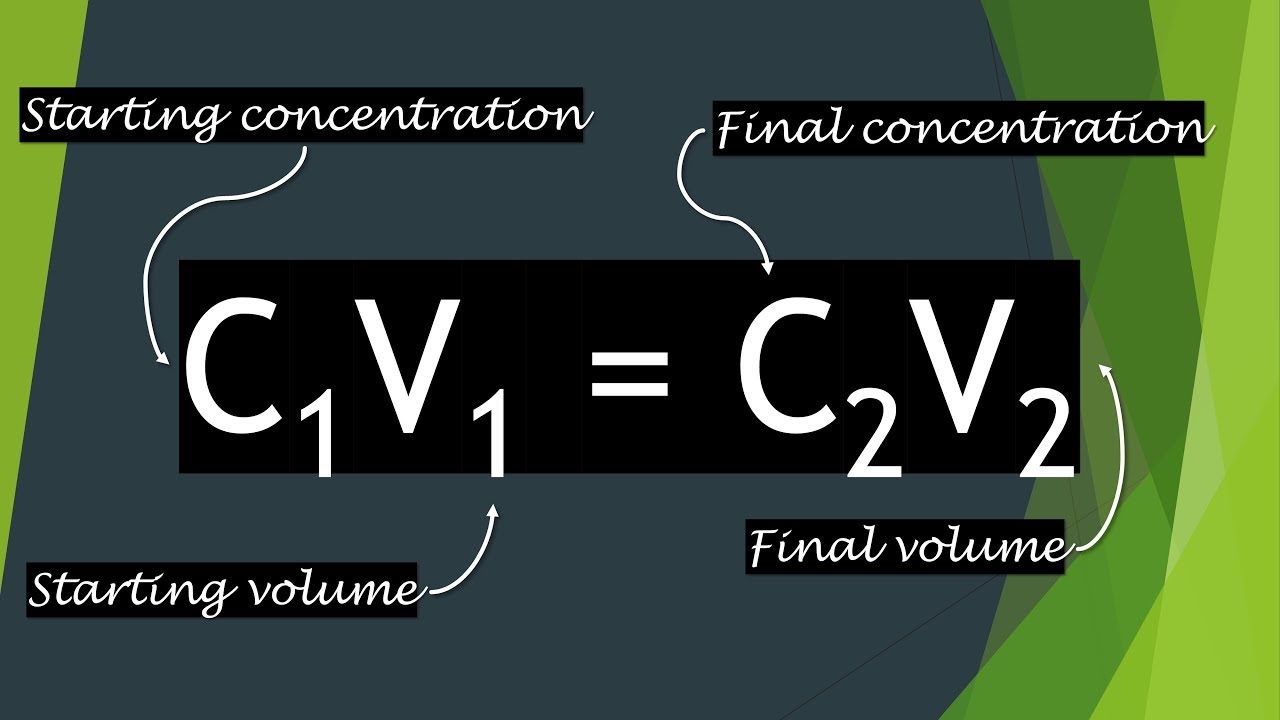
The C1V1 = C2V2 Equation Explained

Dilution Explained

Lab Demonstration | Acid - Base Titration.

Another Stoichiometry Example in a Solution

Dilution Problems, Chemistry, Molarity & Concentration Examples, Formula & Equations
5.0 / 5 (0 votes)
Thanks for rating: