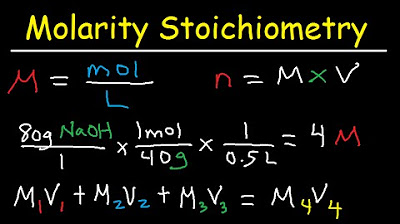Dilution Problems, Chemistry, Molarity & Concentration Examples, Formula & Equations
TLDRThe video script delves into the concept of dilution problems, explaining how to calculate and manipulate the concentration of solutions. It introduces the fundamental equation m1v1 = m2v2, where m represents molarity and v represents volume. The script provides a step-by-step guide on how to decrease or increase the concentration of a solution by either adding water (dilution) or evaporating it. It also covers how to find the new concentration when two solutions are mixed, emphasizing the weighted average approach when dealing with solutions of the same substance. The video includes several problems to illustrate the process, enhancing the viewer's understanding of dilution and concentration calculations.
Takeaways
- 🧪 Dilution problems can be solved using the equation m1v1 = m2v2, where m represents molarity (concentration) and v represents volume.
- 💧 To decrease the concentration of a solution, add water or another solvent to increase the volume, thus reducing the molarity proportionally.
- ⚗️ To increase the concentration of a solution, you can either add more solute (like salt) or remove the solvent by evaporation, which decreases the volume.
- 📉 When diluting, if the volume doubles, the concentration is halved. This principle applies for any proportional change in volume and concentration.
- 📈 To find the original volume of a solution before dilution, use the equation with the known final volume and concentration, then solve for the original volume (v1).
- 💧 The amount of water added to a solution can be found by subtracting the original volume (v1) from the final volume (v2).
- 🌞 For solutions with different substances, when mixed, the final concentration will be a weighted average based on the volumes and concentrations of the individual solutions.
- 🔄 When two solutions with the same solute are mixed, the resulting concentration is the total moles of solute divided by the total volume of the mixture.
- ⚖️ The final concentration of a mixture of solutions with the same solute is influenced more by the solution with the larger volume, if the volumes are not equal.
- 📊 The concept of moles (n) being equal to the product of molarity (c) and volume (v) is central to understanding how concentration changes with volume in a solution.
- 📌 When calculating the new concentration after mixing or diluting solutions, it is crucial to ensure that the units for volume (e.g., milliliters, liters) are consistent across all measurements.
Q & A
What is the basic equation used to solve dilution problems?
-The basic equation used to solve dilution problems is m1V1 = m2V2, where m represents molarity or concentration, and V represents volume.
How does adding water to a solution affect its concentration?
-Adding water to a solution dilutes it, thus reducing the concentration. The more water you add, the lower the concentration becomes.
If you want to increase the concentration of a solution, what are the two methods you can use?
-To increase the concentration of a solution, you can either add more solute (like salt) or remove some solvent (like water), for example, through evaporation.
What is the relationship between the volume and concentration of a solution when it is diluted?
-When a solution is diluted, the volume increases and the concentration decreases proportionally. If the volume is doubled, for instance, the concentration will be halved.
How do you calculate the original volume of a solution if you know the final volume and the new concentration after dilution?
-You can use the dilution equation m1V1 = m2V2. By knowing the new concentration (m2) and the final volume (V2), you can solve for the original volume (V1).
What happens to the volume and concentration when water is evaporated from a solution?
-When water evaporates from a solution, the volume decreases and the concentration increases. The amount of solute remains the same, but there is less solvent.
How do you find the new volume of a solution after a certain amount of water has been added?
-You simply add the volume of water added to the original volume of the solution to get the new total volume.
When two solutions of the same substance are mixed, how is the new concentration determined?
-The new concentration is determined by a weighted average of the two solutions. It is calculated by adding the product of the concentration and volume of each solution and then dividing by the total volume of the mixture.
What is the formula used to calculate the new concentration when two solutions with different concentrations of the same substance are mixed?
-The formula used is m1V1 + m2V2 = m3V3, where m1 and m2 are the initial concentrations, V1 and V2 are the initial volumes, and m3 is the new concentration after mixing in a total volume of V3.
How does the final volume of a mixture affect the new concentration when two solutions are mixed?
-The final volume (V3) determines the extent to which the concentrations of the individual solutions are averaged. A larger final volume will result in a more diluted mixture, while a smaller final volume will concentrate the solute more.
In the context of the script, why would the concentration of a solution be reduced to 0.2 molar from an original 0.8 molar by adding 375 milliliters of water?
-The concentration is reduced because the volume of the solution is increased by the addition of water. Since the amount of solute remains the same, but the total volume increases, the concentration (molarity) of the solute in the solution decreases.
Outlines
🧪 Understanding Dilution and Concentration
This paragraph introduces the concept of dilution problems and their solutions using the equation m1v1 = m2v2, where m stands for molarity or concentration and v for volume. The importance of matching units for volume is emphasized. The process of decreasing concentration by adding water to a solution is explained, as well as increasing concentration by adding more solute or removing solvent through evaporation. The video then dives into solving a series of dilution problems using the given equation, illustrating how to find the original volume of a solution, the amount of water added, and the new volume after evaporation.
💧 Calculating Water Added and Removed
The second paragraph focuses on calculating the amount of water added to a solution to achieve a desired concentration and the amount of water removed through evaporation. It demonstrates the process of finding the original volume of a solution, the volume change, and the calculation of water added or removed to alter the solution's concentration. The paragraph also provides examples of how to use the dilution equation to solve for the new volume after evaporation and the amount of water that was removed from a solution.
📏 Finding New Volumes and Concentrations
This paragraph deals with finding the new volume and concentration of solutions after water has been added or removed. It explains how to calculate the new volume by adding the volume of water to the initial volume of the solution. The paragraph also addresses how to find the new concentration after dilution by dividing the product of the original concentration and volume by the new total volume. An example is provided to illustrate the calculation of the new concentration of a sodium hydroxide solution after water is added.
🔍 Mixing Solutions with Different Concentrations
The fourth paragraph discusses the process of finding the new concentration when two solutions with different concentrations are mixed. It outlines the calculation of the final volume of a mixture and explains how the concentrations of the individual solutions will change upon mixing. The paragraph provides a formula for calculating the new concentration (m1v1 = m2v2) and applies it to find the new concentration of sodium chloride and potassium bromide after they are mixed. It also highlights that the final concentration will be less than the highest initial concentration and greater than the lowest, depending on the volumes of the solutions mixed.
🔬 Weighted Average Concentration of Mixed Solutions
The final paragraph explores the concept of weighted average concentration when mixing two solutions with the same solute. It explains that the new concentration will be a weighted average of the initial concentrations, depending on the volumes of the solutions mixed. The paragraph modifies the dilution equation to account for the total moles of solute (m1v1 + m2v2 = m3v3) and uses it to find the new concentration of a mixture of calcium chloride solutions with different concentrations. The example demonstrates that the final concentration will be closer to the concentration of the solution with the greater volume.
Mindmap
Keywords
💡Dilution
💡Molarity
💡Volume
💡Concentration
💡Equation m1v1 = m2v2
💡Evaporation
💡Solute
💡Solvent
💡Weighted Average
💡Moles
💡Aqueous Solution
Highlights
The fundamental equation for dilution problems is m1v1 = m2v2, where m represents molarity or concentration and v represents volume.
To decrease the concentration of a solution, dilute it by adding water or another solvent.
Adding water to a solution will result in a decrease in concentration by a factor equal to the increase in volume.
To increase the concentration of a solution, add more solute, such as salt, or remove the solvent through evaporation.
The concentration of a solution can be increased by evaporation, which reduces the volume and thus increases the molarity.
When two solutions are mixed, the resulting concentration is a weighted average of the individual concentrations.
The new concentration after mixing solutions can be found using the formula m1v1 + m2v2 = m3v3.
The volume of a solution increases when water or another solvent is added, leading to a proportional decrease in concentration.
For a dilution problem, the volume increase is directly proportional to the concentration decrease.
The amount of water added to a solution can be calculated by subtracting the original volume from the final volume.
When the concentration of a solution is increased by evaporation, the new volume can be estimated by dividing the original volume by the concentration increase factor.
The change in volume due to evaporation can be determined by comparing the initial and final volumes of the solution.
When water is added to a solution, the concentration decreases, as demonstrated by the decrease from 4.5 molar to 1.761 molar.
Mixing two solutions with different substances results in a new concentration for each substance based on their respective volumes and concentrations.
The final concentration of a mixed solution can be estimated to be between the concentrations of the individual solutions, depending on their volumes.
The concept of moles (n) being equal to concentration (c) times volume (v) is crucial for understanding dilution calculations.
In a weighted average problem, the final concentration is influenced more by the solution with the larger volume.
The final concentration of a mixture of solutions with the same solute can be found using the sum of the product of each solution's molarity and volume, divided by the total volume.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: