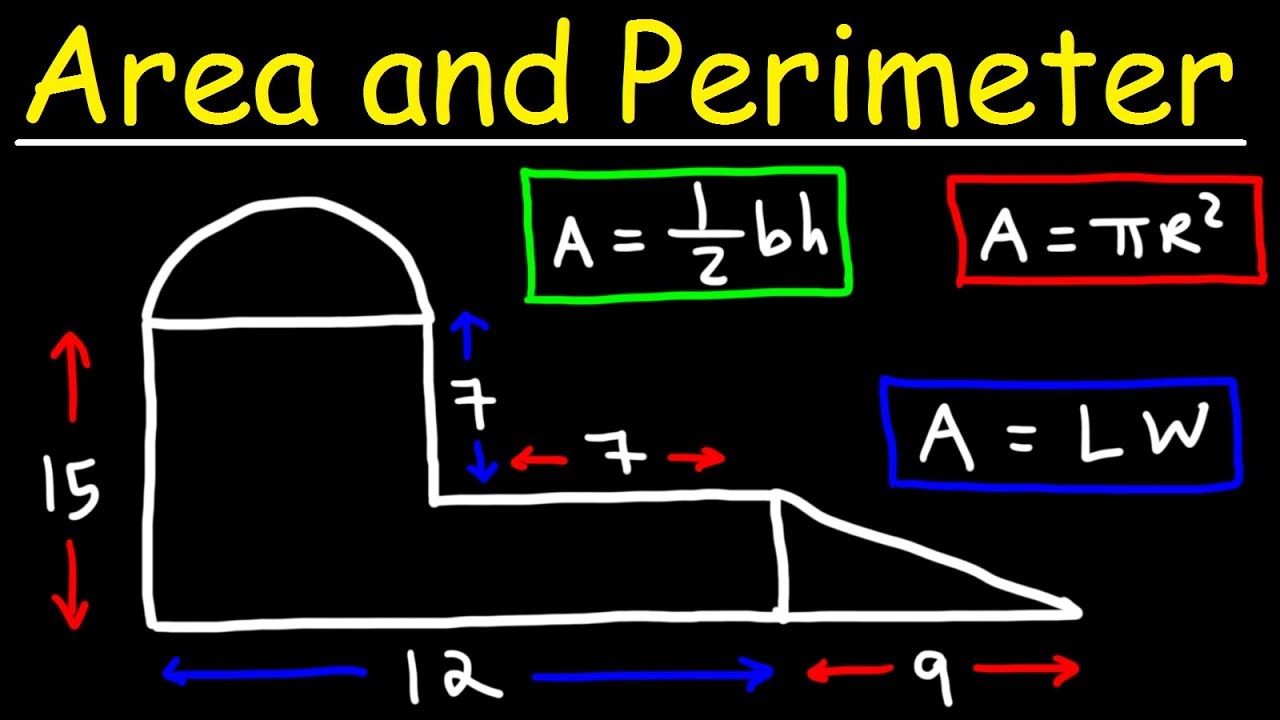
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J

Mr. Jay introduces the topic of finding the area of various shapes, including rectangles, squares, triangles, and circles. He explains that area measures the amount of surface a shape covers and will demonstrate the process for each shape starting with rectangles, then squares, triangles, and finally circles. The first example for rectangles involves using the formula (length × width) with a given length of 6 meters and width of 3 meters to find the area in square meters.

The video script proceeds with detailed examples of calculating areas for rectangles and squares. For rectangles, the formula area = length × width is used with different measurements, such as 19 feet by 5 feet, resulting in an area of 95 square feet. Squares are calculated using the formula area = side length squared, with examples including a square with sides of 8 inches resulting in 64 square inches, and another with 11-meter sides yielding 121 square meters. The script also includes a visual explanation of why the area is calculated as length times width by drawing out the shape and counting square units.

The script then covers the area calculation for triangles, using the formula area = (base × height) / 2. It explains that this formula is derived from the fact that a triangle is half of a rectangle or parallelogram. Examples given include a triangle with an 8-foot base and a 6-foot height, resulting in an area of 24 square feet, and another with a 9-meter base and a 4-meter height, yielding an area of 18 square meters. The script also clarifies that the area calculation involves taking half of the product of the base and height.

The script continues with a more complex example of a triangle where the base is extended, and the height is measured from this extension. The triangle has a base of 5 yards and a height of 11 yards. Despite the unusual drawing, the area is calculated correctly as 27.5 square yards by using the formula area = (base × height) / 2. The script also visually demonstrates how doubling the triangle creates a parallelogram, reinforcing the concept that the area of a triangle is half that of the parallelogram formed by two identical triangles.

The final part of the script addresses the area calculation for circles using the formula area = πr², where π (pi) is a constant approximately equal to 3.14, and r is the radius of the circle. The script provides an example with a circle having a radius of 9 centimeters, resulting in an area of 81π square centimeters, which can be approximated to 254.34 square centimeters using the value of π as 3.14. Additionally, the script explains the difference between diameter and radius and how to use the diameter to find the area of a circle, as demonstrated with a circle having a diameter of 12 feet.

The script concludes by summarizing the methods for finding the areas of rectangles, squares, triangles, and circles. It reiterates the importance of using the correct formulas and understanding the geometric principles behind the calculations. The video aims to ensure that viewers have a clear understanding of how to calculate areas for these basic shapes and encourages them to apply these methods in practice. The script ends with a note of thanks and a sign-off until the next video.