Area for Kids

Homeschool Pop
3 Oct 201808:57
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video introduces the concept of area, distinguishing it from perimeter and focusing on the space inside shapes. It demonstrates how to calculate the area of squares and rectangles using square units and multiplication, with examples including a 6x1 rectangle resulting in 6 square feet and a 3x3 square yielding 9 square centimeters. The script also mentions the importance of the squared unit in area measurements and hints at more complex shapes like circles and triangles, inviting viewers to explore further in the fascinating world of mathematics.

Takeaways
  • 📏 Area is the measure of the space inside a shape, as opposed to the perimeter, which is the measure of the space around a shape.
  • 🎲 The script introduces a game called 'What's the Area?' to engage the audience in learning about the concept of area.
  • 🔲 To find the area of a square, you count the number of square units inside the shape, as demonstrated with a 4x4 square.
  • 📏 For a rectangle, the area is also found by counting the square units, as shown with a 5x1 rectangle.
  • 🧩 The area of an irregular shape is determined by counting the square units inside it, as exemplified with a shape containing twelve square units.
  • 🔢 When the units inside a shape are not visible, you can find the area by using multiplication.
  • 📐 The area of a rectangle or square is calculated by multiplying the length by the width.
  • 📏 For a rectangle that is 6 feet long and 1 foot wide, the area is found by multiplying 6 by 1, resulting in 6 square feet.
  • 🔢 A square with sides of 3 centimeters each has an area of 9 square centimeters, found by multiplying 3 by 3.
  • 📏 A rectangle that is 4 meters long and 2 meters wide has an area of 8 square meters, calculated by multiplying 4 by 2.
  • 📝 The area of a shape is always expressed in square units, indicated by the term 'squared' or the symbol '²'.
  • 📚 The script hints at more complex shapes like circles and triangles, suggesting that different formulas are needed for their areas, beyond the basics covered for rectangles and squares.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the concept of area in geometry, specifically how to find the area of different shapes.

  • What is the difference between area and perimeter?

    -Area refers to the space inside a shape and is measured in square units, while perimeter is the space around a shape and is measured in linear units.

  • What is the area of a square with four square units inside it?

    -The area of the square is four square units, as it has four individual square units inside it.

  • How is the area of a rectangle calculated?

    -The area of a rectangle is calculated by multiplying its length by its width.

  • What is the area of a rectangle that is 6 feet long and 1 foot wide?

    -The area of the rectangle is 6 square feet, found by multiplying 6 (length) by 1 (width).

  • How many square units are in a square that is 3 centimeters long on each side?

    -The area of the square is nine square centimeters, as it is calculated by multiplying 3 (side length) by 3.

  • What is the area of a rectangle that is 4 meters long and 2 meters wide?

    -The area of the rectangle is eight square meters, which is the result of multiplying 4 (length) by 2 (width).

  • What does the term 'squared' signify in the context of area?

    -The term 'squared' signifies that the measurement is in square units, indicating the space inside a shape.

  • Why is multiplication used to find the area of a shape?

    -Multiplication is used to find the area of a shape because it combines the length and width (or side lengths for a square) to determine the total space inside the shape.

  • What is a quick tip mentioned in the video about expressing the area of a shape?

    -A quick tip mentioned in the video is that when expressing the area of a shape, the unit of measurement should be followed by 'squared' to indicate the space inside the shape.

  • What is the significance of learning about area in the context of the warehouse example?

    -Learning about area is significant as it helps in practical applications, such as determining the space available in a warehouse by multiplying its length and width.

Outlines
00:00
📏 Introduction to Area and Perimeter

The video begins with an introduction to the concept of area, explaining that it is the measure of the space inside a shape, which is distinct from the perimeter, the space around the shape. The video aims to educate viewers on how to determine the area of various shapes, starting with a simple game called 'What's the Area?' The first example given is a square with four square units, indicating that the area is the number of square units inside the shape. The video continues to explore the area of a rectangle and an irregular shape, encouraging viewers to count the units to find the area.

05:02
🔢 Calculating Area with Multiplication

This paragraph delves into the method of calculating the area of shapes using multiplication. It clarifies that for rectangles and squares, the area can be found by multiplying the length by the width. The video provides examples of a rectangle with a length of six feet and a width of one foot, resulting in an area of six square feet, and a square with sides of three centimeters, yielding an area of nine square centimeters. The explanation is extended to a rectangle with dimensions of 4 meters by 2 meters, resulting in an area of eight square meters. The video concludes with two tips: the area is always expressed in squared units, and different multiplication formulas are required for shapes like circles and triangles, hinting at the broader scope of the topic.

Mindmap
Keywords
💡Area
Area is defined as the amount of space inside a two-dimensional shape. In the context of the video, area is the focus of the educational content, teaching viewers how to calculate the space inside various shapes such as squares and rectangles. The script uses the concept of area to explain that it is different from perimeter and is measured in square units, as illustrated with the examples of the square with four square units and the rectangle with five square units.
💡Perimeter
Perimeter refers to the total length of the sides of a two-dimensional shape. The video script contrasts perimeter with area, emphasizing that perimeter is the measurement of the space around a shape, while area is the space inside. This distinction is crucial for understanding the different applications of these two geometric concepts.
💡Shape
A shape in the video is a two-dimensional figure with a certain area and perimeter. The script introduces different types of shapes, such as squares and rectangles, and discusses how to calculate their area. The term 'shape' is central to the video's theme, as it is the subject whose area is being explored and calculated.
💡Square Units
Square units are the units of measurement used to express area. In the script, it is explained that area is measured in square units, which is demonstrated by counting the number of these units within a square or rectangle to find its area, such as the four square units inside the square and the five square units inside the rectangle.
💡Square
A square is a specific type of shape with four equal sides and four right angles. The video uses the square to illustrate the concept of area, showing that the area of a square is calculated by multiplying the length of one side by itself, as in the example where a square with sides of three centimeters has an area of nine square centimeters.
💡Rectangle
A rectangle is another type of shape with four sides, where opposite sides are equal and all angles are right angles. The script explains how to find the area of a rectangle by multiplying its length by its width, using an example of a rectangle that is six feet long and one foot wide, which has an area of six square feet.
💡Irregular Shape
An irregular shape in the video refers to a two-dimensional figure that does not have equal sides or angles. The script introduces an irregular shape and challenges the viewer to calculate its area by counting the square units inside, which turns out to be twelve square units, demonstrating the concept of area for non-standard shapes.
💡Multiplication
Multiplication is the mathematical operation used to calculate the area of shapes like squares and rectangles. The video script explains that to find the area, one must multiply the length by the width. This operation is demonstrated multiple times, such as with the rectangle that is six feet by one foot, resulting in an area of six square feet.
💡Length
Length is one of the dimensions of a shape, typically referring to the longer side of a rectangle or the side of a square. In the context of the video, length is used in conjunction with width to calculate the area of a shape through multiplication, as shown in the examples of the rectangle and square.
💡Width
Width is the other dimension of a rectangle, perpendicular to the length. The script uses width in the context of calculating the area of a rectangle by multiplying it by the length, as in the example where a rectangle that is four meters long and two meters wide has an area of eight square meters.
💡Square Feet/Square Meters
Square feet and square meters are units of area measurement used to express the space inside a shape in terms of feet and meters squared, respectively. The video script uses these terms to illustrate the results of area calculations, such as six square feet for a rectangle and nine square centimeters for a square.
Highlights

Introduction to the concept of area and its distinction from perimeter.

Area defined as the space inside a shape, contrasting with perimeter which is the space around a shape.

Engaging the audience with a game called 'What's the Area?' to find the area of a shape.

Demonstration of how to measure the area of a square using square units.

Explanation of the area of a square being four square units.

Transitioning to finding the area of a rectangle using the same square unit method.

Revealing the area of the rectangle as five square units.

Introduction to calculating the area of an irregular shape using square units.

Finding the area of an irregular shape to be twelve square units.

The challenge of finding the area of a shape when you can't see the inside units.

Introducing multiplication as the method to find the area of a shape when units are not visible.

Teaching the formula for finding the area of a rectangle or square by multiplying length by width.

Example calculation of a rectangle's area with a length of six feet and a width of one foot.

Clarification that multiplying a number by one results in the number itself, as shown with six times one.

Illustration of calculating a square's area with each side being three centimeters.

Explanation of the area of a square being nine square centimeters.

Another example of calculating the area of a rectangle with dimensions in meters.

Conclusion that the area of the rectangle is eight square meters.

Highlighting that the area is always expressed in square units, such as square feet or square centimeters.

Mentioning the need for different multiplication equations for the area of circles and triangles.

Encouraging the audience that learning the basics of area is just the beginning of an exciting journey in math.

Practical application of area calculation in determining the space available in a warehouse.

Final thoughts on the importance and excitement of learning about area in mathematics.

Transcripts

Browse More Related Video

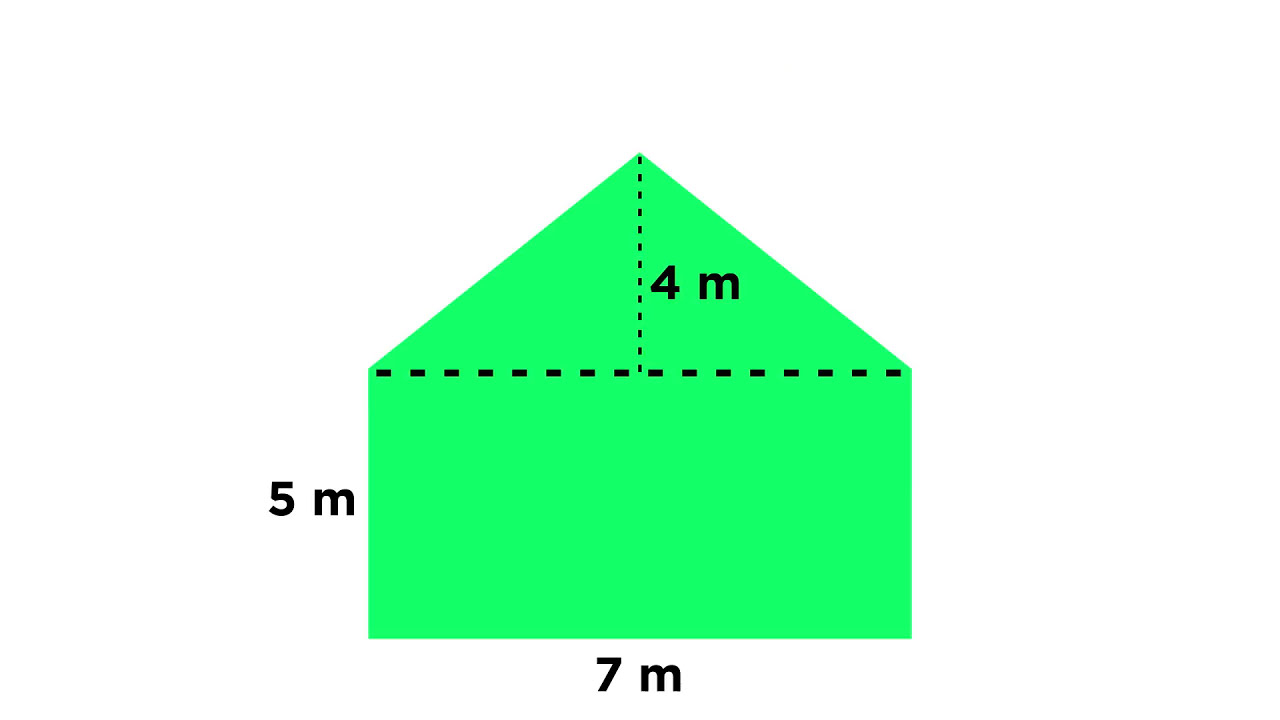
Calculating the Area of Shapes

Math Antics - Area

How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J

Area and Perimeter of Irregular Shapes - Tons of Examples!

Topic 43-Volumes of Solids with Known Cross Sections

Area of an Oblique Triangle - SAS & SSS - Heron's Formula, Trigonometry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Area BasicsMath EducationSquare UnitsRectanglesSquaresMultiplicationShape SpaceCalculation TipsEducational FunGeometry 101