TI-84 Calculator - 10 - Calculating Derivatives and Integrals
TLDRThis tutorial segment introduces the numerical derivative and integral functions on the TI-84 calculator, which are beneficial for students studying calculus. The video explains that while the calculator cannot perform symbolic integration or differentiation, it can calculate numerical derivatives and integrals. The process involves entering a function and specifying points for the calculator to evaluate the slope of the tangent line or the area under the curve. Examples are provided, such as finding the derivative of x squared at different points and integrating x squared from zero to four. The tutorial emphasizes the usefulness of these features for quick calculations and verifying homework solutions.
Takeaways
- 📚 The video tutorial focuses on two functions of the TI-84 calculator: numerical derivative and numerical integral, which are useful for students studying calculus.
- 🛠 The TI-84 calculator is a midline calculator for calculus in the TI series, designed for basic functions rather than heavy-duty calculus tasks.
- 📉 Numerical derivative function calculates the slope of the tangent line to a curve at a specified point, providing a numerical value.
- 📈 Numerical integral function computes the definite integral of a function between two specified numbers, giving an area under the curve.
- 🚫 The calculator does not perform symbolic integration or differentiation, meaning it won't provide the formula for the derivative or integral of a function.
- 🔢 To use numerical derivative, you input the function, the independent variable, and the specific point at which you want to find the derivative.
- 📝 For example, to find the derivative of x^2 at x=2, the calculator will output 4, as 2x evaluated at x=2 equals 4.
- 🔍 The calculator can handle more complex functions for numerical differentiation, such as x^3 - 4x + 5 at x=-1, yielding a result close to -1.
- 📐 Numerical integration requires specifying a function, the independent variable, and the lower and upper bounds of integration.
- 📊 The calculator provides an approximate area under the curve for definite integrals, such as integrating x^2 from 0 to 4, resulting in 21.3.
- 🔧 The numerical functions on the TI-84 are useful for quick checks or verifications of work, especially for standardized tests or homework practice.
Q & A
What are the two functions discussed in the TI 84 tutorial?
-The two functions discussed are numerical derivative and numerical integral.
Why might someone skip this section of the tutorial if they haven't studied calculus?
-They can skip it because the section is not essential for understanding future content and requires knowledge of calculus.
What is the purpose of the numerical derivative function on the TI 84 calculator?
-The numerical derivative function calculates the slope of the tangent line to a curve at a specified point.
How does the numerical integral function differ from a symbolic integral?
-The numerical integral calculates the definite integral between two numbers, providing an area under the curve, whereas a symbolic integral would provide the antiderivative function.
What is the calculator's limitation when it comes to integrals and derivatives?
-The calculator cannot perform symbolic integration or differentiation; it can only calculate numerical derivatives and integrals.
How does the TI 84 calculator calculate the derivative of a function at a specific point?
-It calculates the derivative by plugging in the specified point into the function and determining the slope of the tangent line at that point.
What is the process of using the numerical derivative function on the TI 84?
-You specify the function, the independent variable, and the point at which you want to calculate the derivative, and the calculator provides the slope of the tangent line at that point.
How does the TI 84 calculator perform numerical integration?
-You specify the function, the independent variable, and the lower and upper bounds of integration, and the calculator calculates the area under the curve between those bounds.
What is the significance of being able to calculate numerical integrals and derivatives on the TI 84 calculator?
-It allows students to quickly verify their work and check answers, which is helpful for standardized tests or homework practice.
Why might a student use the numerical derivative feature on the TI 84 calculator?
-A student might use it to understand the slope of a function at a specific point or to verify their manual calculations of derivatives.
Outlines
📚 Introduction to Numerical Derivatives and Integrals on TI 84
This paragraph introduces the concept of numerical derivatives and integrals on the TI 84 calculator, which are useful tools for students studying calculus. It explains that while the TI 84 is not designed for heavy-duty calculus, it does offer basic functions for calculating numerical derivatives and integrals. The paragraph clarifies that numerical operations involve inputting a function and obtaining a numerical result, such as the slope of the tangent line at a specific point for derivatives, or the area under the curve between two points for integrals. It also notes that the calculator cannot perform symbolic integration or differentiation, which would require a more advanced calculator like the TI-89.
🔍 Demonstrating Numerical Derivative Calculation on TI 84
The second paragraph provides a step-by-step demonstration of how to calculate the numerical derivative of a function using the TI 84 calculator. It uses the example of the function x squared and explains the process of inputting the function, specifying the variable of differentiation (x), and choosing a point at which to calculate the derivative (e.g., x = 2 or x = 5). The paragraph illustrates how the calculator provides the slope of the tangent line at the specified point, which corresponds to the derivative value. It also mentions that more complex functions can be used for this calculation, showcasing the calculator's capability to handle polynomials and emphasizing its utility for checking work in calculus.
Mindmap
Keywords
💡TI 84 calculator
💡Numerical derivative
💡Numerical integral
💡Calculus
💡Derivative
💡Integral
💡Symbolic calculation
💡Definite integral
💡Tangent line
💡Area under the curve
Highlights
The TI 84 calculator has functions to calculate numerical derivatives and integrals.
Numerical derivatives and integrals are topics covered in detail in calculus.
The calculator is not intended for heavy duty calculus but provides basic functions.
Numerical derivative function calculates the slope of the tangent line at a specified point.
Numerical integral function calculates the area under the curve between two points.
The calculator cannot take integrals and derivatives symbolically in terms of X.
Example given of calculating the derivative of x^2 at x=2, result is 4.
Changing the point to x=5 gives a derivative of 10 for the function x^2.
More complex functions like x^3 - 4x + 5 can also have their derivatives calculated.
Numerical derivative of the complex function at x=-1 is approximately -1.
Numerical integration is covered next in the tutorial.
Example of numerically integrating x^2 from 0 to 4, result is 21.3.
Integral of x^2 from 0 to 4 is calculated by evaluating 1/3x^3 at the bounds.
More complex functions like x^2 - sin(x) can be integrated over an interval.
Numerical integration can be used to quickly verify work on a GRE or standardized test.
The calculator is a handy tool for quickly calculating numerical integrals and derivatives.
Transcripts
Browse More Related Video

Casio FX-991EX Differentiation Tutorial: How to Find Derivatives on Your Casio Calculator

Definite integrals (area under a curve) with GDC [IB Maths AI SL/HL]

TI-89 Calculator - 03 - Calculating Indefinite and Definite Integrals in Calculus
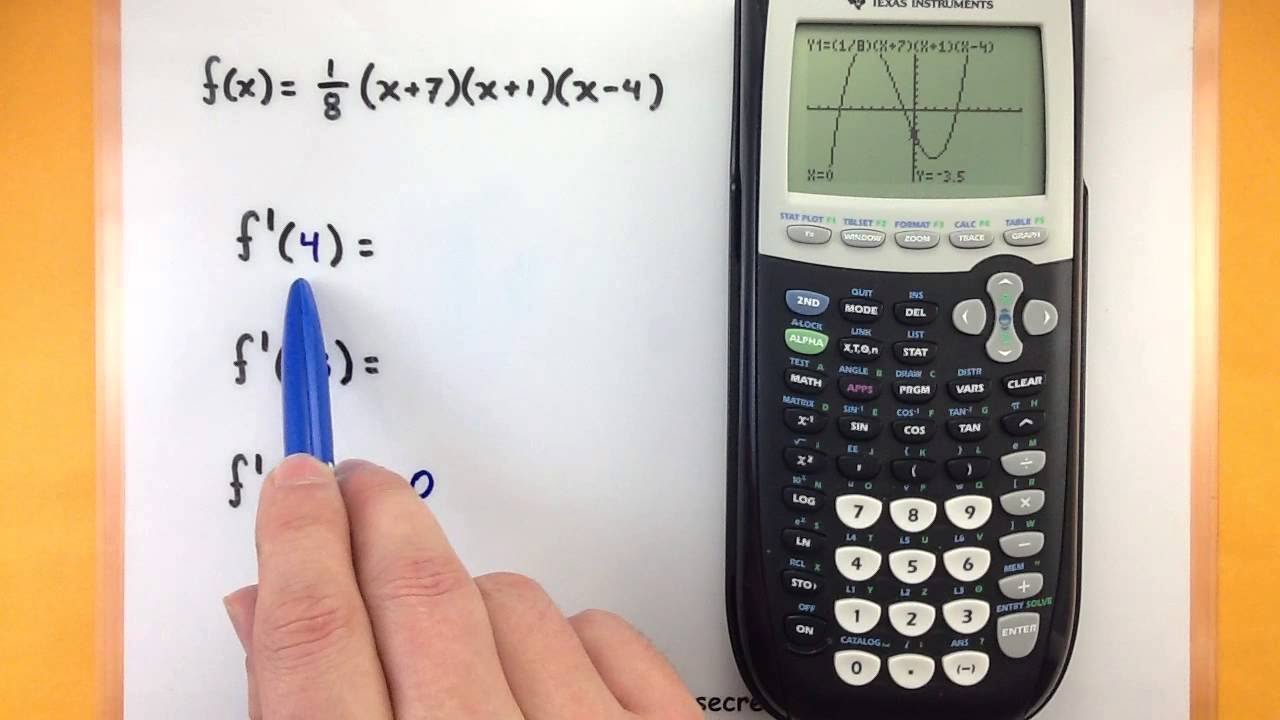
Calculus - Finding the derivative at a point using a Ti-83 or 84 calcululator

INTEGRATION PART 2: CALCULATOR TECHNIQUES ON INDEFINITE INTEGRATION OF TRIGONOMETRIC FUNCTIONS

Using the TI 83/84 calculator to find a derivative
5.0 / 5 (0 votes)
Thanks for rating: