Definite integrals (area under a curve) with GDC [IB Maths AI SL/HL]
TLDRThe video script offers an informative guide on how to find the area under a curve, specifically for definite integrals, using a graphical display calculator (GDC). The presenter explains the process of integration and how to calculate the area between a curve and the x-axis when the bounds are known. The script demonstrates two methods for finding the integral: one involves graphing the function and using the calculator's integral function to find the area from the lower bound 'a' to the upper bound 'b'. The other method is a direct approach, inputting the function and bounds into the calculator to compute the integral. The presenter also provides a tip to always write out the integral when using a calculator, even on exams. Examples are given using functions such as x squared and x squared minus x, with the calculator providing the area under the curve from specified intervals. The script emphasizes the ease and utility of using a calculator for these calculations.
Takeaways
- 📈 To find the area under a curve, one can use integration techniques, specifically definite integrals, which require knowing the start and end points of the area in question.
- 📘 The process involves calculating the integral of a function, denoted as ∫f(x)dx from point a to point b, where 'a' and 'b' are the bounds of the area.
- 📊 The definite integral represents the exact area under the curve of a function without the need to add an arbitrary constant 'C'.
- 📌 The formula for the area under a curve from a to b is given by ∫y dx from a to b, where 'y' is the function f(x).
- 🖋️ When taking an exam, it's important to write out the full integral, including the 'dx', even if you're using a calculator to solve it.
- 📱 Calculators can be used to find the area under a curve either by graphing the function and then calculating the integral, or by directly entering the function and bounds.
- 📐 The TI-Inspire and TI-84 calculators are examples of devices that can graph functions and calculate integrals.
- 📝 The process of graphing the function and then finding the integral can be done through the calculator's analyze function, where you input the lower and upper bounds of integration.
- 🔢 For a direct calculation without graphing, you can use the calculator's numerical integration function, inputting the function, lower bound, upper bound, and 'dx'.
- 🗂️ The calculator can also convert the result into a fraction, providing a more exact representation of the integral's value.
- 🎓 Examples provided in the script include finding the area under the curve y = x^2 from 0 to 1, and y = x^2 - x from 2 to 3, with the calculator yielding approximate values of 0.333 and 3.83, respectively.
- 📉 The process of finding the area under a curve using a calculator is straightforward and efficient, providing a valuable tool for students and professionals in calculus.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is how to find the area under a curve, specifically using a graphical display calculator to calculate definite integrals.
What is a definite integral?
-A definite integral is an integral that has defined limits of integration, meaning you know exactly where to start and where to finish the calculation of the area under the curve.
What does 'dx' represent in the context of an integral?
-'dx' represents an infinitesimally small change in the x variable and is used to denote integration in calculus.
Why is it important to write out the integral even when using a calculator?
-Writing out the integral is important because it shows the process of the calculation, which is often required in an exam setting. It also helps to ensure that you've correctly identified the function to be integrated and its bounds.
How can you find the area under a curve using a calculator?
-You can find the area under a curve using a calculator by either graphing the function and using the calculator's integral function to find the area between the curve and the x-axis, or by directly entering the function and the bounds into the calculator's numerical integration function.
What is the integral of x squared from 0 to 1?
-The integral of x squared from 0 to 1 is approximately 0.333, which is equivalent to one-third.
What is the function being integrated in the second example provided in the transcript?
-The function being integrated in the second example is f(x) = x squared minus x.
How does the process of finding the area under a curve using a calculator differ from doing it by hand?
-Using a calculator simplifies the process by providing numerical integration tools that automatically calculate the integral within the given bounds. By hand, one would have to manually apply integration techniques and formulas to find the area.
What is a 'pro tip' mentioned in the transcript for doing calculus exams?
-The 'pro tip' mentioned is to always write out the integral completely, including the 'dx', even when using a calculator to find the solution.
What does the calculator display as the result of the integral from 2 to 3 of the function x squared minus x?
-The calculator displays the result of the integral from 2 to 3 of the function x squared minus x as approximately 3.83.
How can the calculator help visualize the process of finding the area under a curve?
-The calculator can graph the function, allowing you to visually identify the area you want to integrate. It can then calculate the integral either by analyzing the graph or by directly entering the function and bounds.
What is the significance of the bounds 'a' and 'b' in the context of a definite integral?
-The bounds 'a' and 'b' define the limits of the definite integral, indicating the starting and ending points for the calculation of the area under the curve.
Outlines
📈 Understanding Definite Integrals and Calculating Area Under a Curve
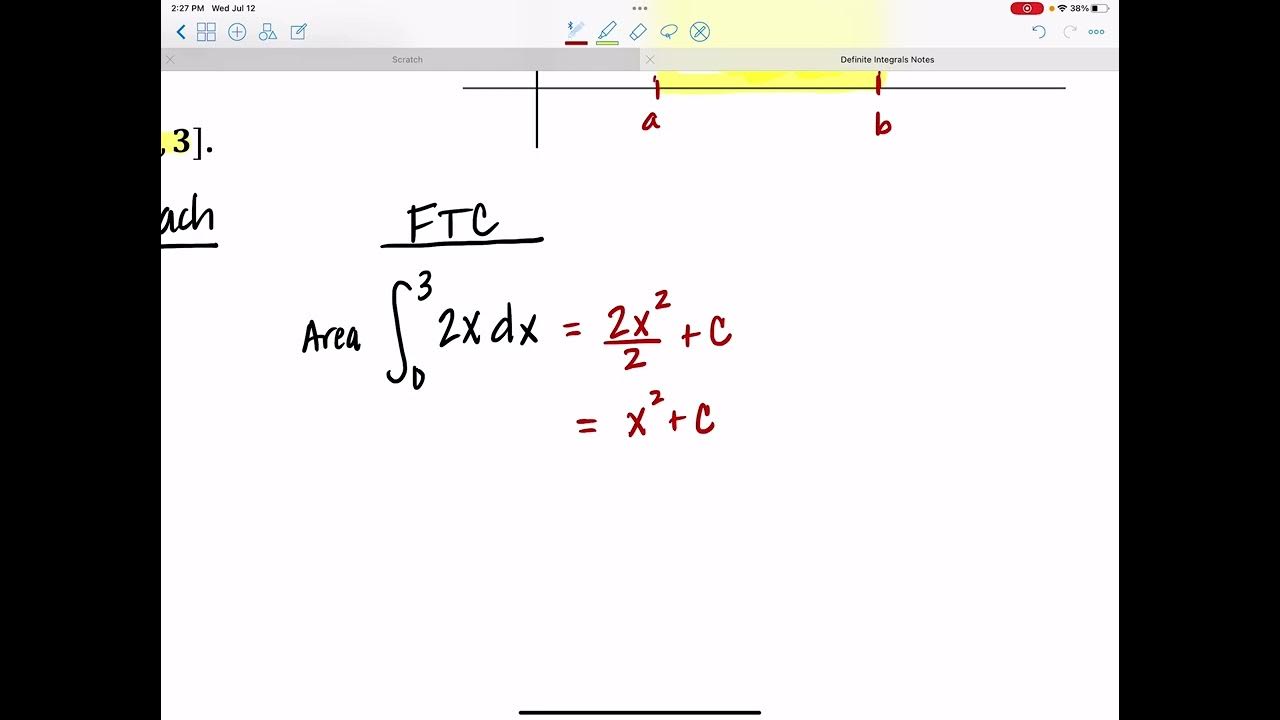
This paragraph introduces the concept of definite integrals, which are used to calculate the exact area under a curve between two points, a and b. The speaker emphasizes the importance of writing out the integral formula even when using a calculator, highlighting the process of defining the integral with bounds and the absence of the 'plus c' notation when dealing with definite integrals. The explanation includes a practical example of finding the area under the curve of the function f(x) = x^2 from 0 to 1 using a graphical calculator, and the importance of including 'dx' in the integral notation.
🔢 Calculating Integrals with and Without Graphing on a Calculator
The second paragraph demonstrates two methods for calculating integrals using a calculator: with and without graphing. The speaker first shows how to graph the function x^2 and then use the calculator's analyze function to find the integral from 0 to 1, obtaining an approximate result of 0.333 or one-third. The alternative method involves directly inputting the integral into the calculator, using the numerical integral function, and entering the bounds and function to get the result. The speaker also illustrates this process with the function f(x) = x^2 - x, calculating the area under the curve from 2 to 3, and obtaining an approximate result of 3.83. The paragraph concludes by noting that both methods yield the same answer and emphasizes the ease of using a calculator for these calculations.
Mindmap
Keywords
💡Integral
💡Graphical Display Calculator (GDC)
💡Definite Integrals
💡Area Under the Curve
💡Function
💡Numerical Integration
💡Upper and Lower Bounds
💡Calculus
💡Examination (Exam)
💡Sketching
💡Conversion to Fraction
Highlights
The process of finding the area under a curve using a graphical display calculator is explained in detail.
Integration is used to find the area under a curve for definite integrals where the start and end points are known.
The definite integral is defined as the area between a curve y=f(x) and the x-axis where f(x) is greater than zero.
The equation for the definite integral is ∫ from a to b of f(x) dx, without the +C term.
The area under the curve from a to b is represented as ∫ from a to b of y dx.
When doing calculus on an exam, it's important to write out the full integral even if using a calculator.
Two methods are demonstrated for finding the integral on a calculator: graphing and direct calculation.
The TI-Inspire and TI-84 calculators can both be used to find integrals using the methods shown.
First, the function is graphed on the calculator, then the integral is calculated from the specified bounds.
Alternatively, the integral can be calculated directly on the calculator without graphing the function first.
The calculator can perform a numerical integral to find the area under the curve.
The integral of x^2 from 0 to 1 is demonstrated, with the result being approximately 0.333 or 1/3.
The integral of x^2 - x from 2 to 3 is calculated, with the result being approximately 3.83.
The calculator can convert the result to a fraction, in this case showing the answer as 1/3.
The process is shown step-by-step for clarity, with the final answer presented clearly.
The use of a calculator makes finding the area under a curve relatively straightforward and easy to understand.
The video provides a helpful guide for students learning calculus and how to use a calculator to solve integrals.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: