College Physics 1: Lecture 2 - Mathematics Review (Part 2)

This section of the lecture introduces the concepts of direct and inverse relationships in mathematics. Direct relationships, where two variables increase or decrease together, are denoted by the Greek symbol alpha (α), indicating proportionality. The equation y = mx represents a direct relationship, with m as the constant of proportionality. An inverse relationship is depicted when one variable increases as the other decreases, expressed as y = k/x, with k as the constant. The lecture also covers the equation of a line, y = mx + b, highlighting the y-intercept (b) and the slope (m), which is determined by the change in x (Δx) and y (Δy), or 'rise over run'. The summary emphasizes the graphical representation of these relationships and their mathematical equations.

The second paragraph delves deeper into the equation of a line, explaining the significance of the slope and y-intercept. It then transitions into a discussion on the areas and volumes of various geometric shapes, such as rectangles, boxes, triangles, circles, spheres, and cylinders. For rectangles and boxes, the formulas for calculating area and surface area are presented, along with the volume calculation for three-dimensional shapes. The importance of understanding these geometric principles is highlighted, as they are fundamental in physics and mathematics.

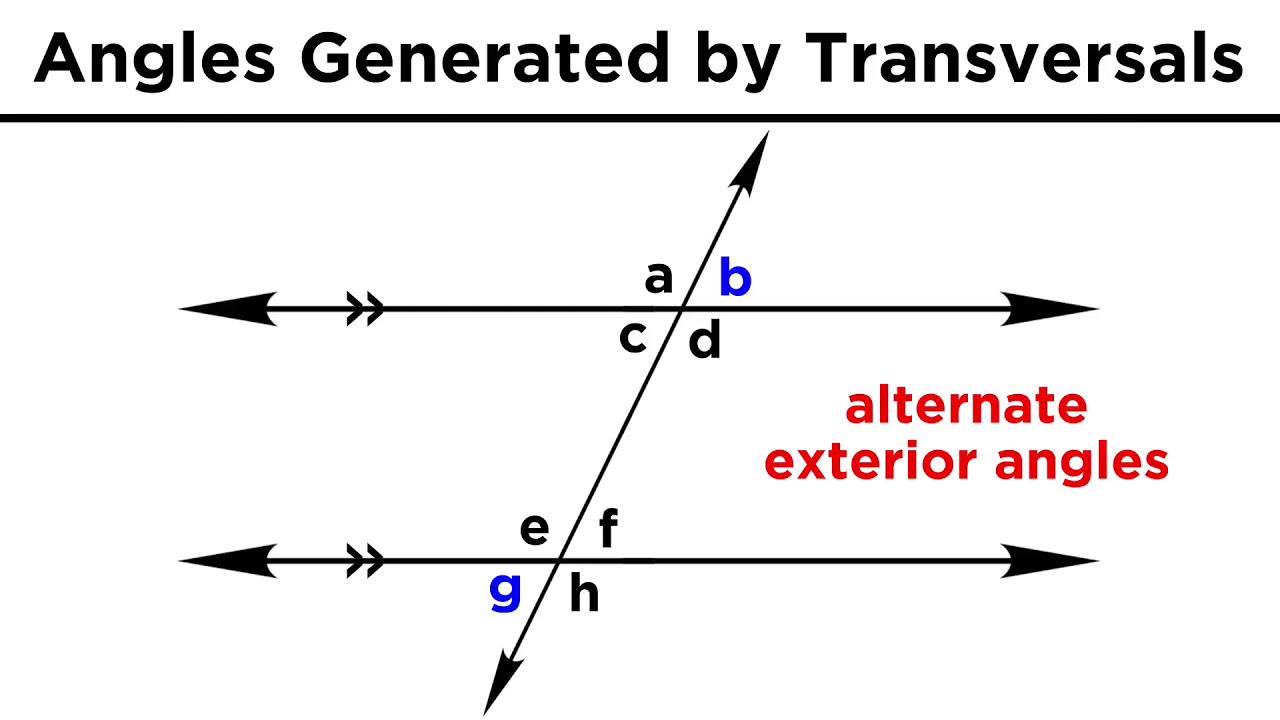
This paragraph explores plane geometry, focusing on the relationships between angles formed by intersecting lines and parallel lines cut by a transversal. It explains that opposite angles created by intersecting lines are equal, and the same is true for corresponding angles, alternate interior angles, and alternate exterior angles when two parallel lines are involved. The concept of supplementary angles, which sum up to 180 degrees, is also discussed, including their occurrence in various geometric configurations such as adjacent angles on a straight line, same side angles, and angles within a triangle. The summary underscores the importance of recognizing these angle relationships in solving geometry problems.

The lecture continues with a detailed look at special cases of angles, particularly when dealing with inclined planes and right triangles. It explains that when two angles are perpendicular to the sides of each other, they are equal. This is demonstrated through an example using a triangle with angles theta and phi. The paragraph also revisits right triangles, emphasizing the Pythagorean theorem for calculating the hypotenuse when two other sides are known. The importance of understanding these angle relationships and their applications in physics problems is highlighted.

This section introduces the application of trigonometric functions—sine, cosine, and tangent—in the context of right triangles. The lecture explains the use of SOHCAHTOA as a mnemonic for remembering the definitions of these functions: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent). It also touches on the use of inverse trigonometric functions to find angles when the sides of a triangle are known. The summary emphasizes the practicality of these functions in solving for unknown sides or angles in right triangles.

The final paragraph presents two practical examples of applying trigonometric functions to solve real-world problems. The first example involves calculating the length of a ramp needed to load a couch into a truck bed, using the sine function to find the hypotenuse of a right triangle formed by the ramp and the truck bed. The second example demonstrates how to use the tangent function to find an unknown angle in a triangle when the lengths of the opposite and adjacent sides are known. The summary illustrates the step-by-step process of solving these problems, emphasizing the importance of rearranging equations and using inverse functions to find unknown angles.

The lecture concludes with a brief mention of upcoming topics, such as significant figures and scientific notation, before diving deeper into physics concepts like position, velocity, and acceleration. The summary serves as a transition from the mathematical review to the core physics content, setting the stage for further exploration into the subject matter.