Continuity Equation
TLDRIn this AP Physics essentials video, Mr. Andersen explains the continuity equation, a principle derived from the conservation of mass in fluids. He illustrates how the mass flow rate remains constant through a system, such as a fire hose, and how changes in diameter or the addition of a nozzle affect the fluid's velocity. The video demonstrates the mathematical representation of the equation, showing that the product of the cross-sectional area and velocity remains constant. Practical examples, including a PHET simulation, clarify the concept, and a step-by-step problem-solving approach is presented to calculate the velocity at different points in the hose, emphasizing the importance of consistent fluid density.
Takeaways
- 🚒 The continuity equation is an application of the conservation of mass in fluids, meaning the mass flow rate in equals the mass flow rate out.
- 🌀 If the diameter of a pipe or hose is changed, such as with a nozzle, the velocity of the fluid increases to maintain the same mass flow rate.
- 🧩 The continuity equation can be represented in two ways: by mass flow rate or by volume flow rate (volumetric flow rate).
- 📏 For mass flow rate, the equation is density × area × velocity, while for volume flow rate, it simplifies to area × velocity since density remains constant.
- 💧 An example illustrates that decreasing the cross-sectional area of a pipe increases the velocity of the fluid to maintain the same flow rate.
- 📚 The equation A1V1 = A2V2 demonstrates that the product of the area and velocity before and after a restriction (like a nozzle) remains constant.
- 📏 To use the continuity equation, one must know the cross-sectional area and velocity at any point in the fluid path, assuming consistent fluid density.
- 🔢 An example problem shows how to calculate the velocity of water coming out of a restricted nozzle using the continuity equation and basic geometry to find the area.
- 📐 Geometry is used to calculate the area of the cross-section when given the diameter of a pipe or nozzle, using the formula πr^2 where r is the radius.
- 🔄 The script includes a practical example of how the continuity equation can be applied to calculate the velocity of water in a fire hose with a restricted nozzle.
- 🎓 The video aims to teach viewers how to make flow calculations based on the continuity equation, providing a clear demonstration and explanation.
Q & A
What is the continuity equation in the context of fluid dynamics?
-The continuity equation in fluid dynamics is an application of the conservation of mass principle, stating that the mass flow rate entering a pipe or hose is equal to the mass flow rate exiting it, regardless of changes in the cross-sectional area or velocity of the fluid.
How does the continuity equation relate to the conservation of mass in fluids?
-The continuity equation is a direct application of the conservation of mass principle to fluids, ensuring that the mass of fluid entering a system is conserved and equal to the mass exiting the system, even when the fluid's velocity or cross-sectional area changes.
What happens to the velocity of a fluid when the cross-sectional area of a pipe decreases?
-When the cross-sectional area of a pipe decreases, the velocity of the fluid increases to maintain the same mass flow rate, as dictated by the continuity equation.
What are the two common ways to represent the continuity equation?
-The continuity equation can be represented in two ways: as the mass flow rate, which includes density, area, and velocity, or as the volume flow rate, which excludes density and is simply the cross-sectional area times the velocity.
How does the density of a fluid factor into the continuity equation?
-In the mass flow rate representation of the continuity equation, the density of the fluid is a key factor, as it multiplies the cross-sectional area and the velocity to give the mass flow rate. However, for incompressible fluids like water, the density often remains constant and can be omitted, simplifying the equation to just the cross-sectional area times the velocity.
Can you provide an example of how the continuity equation is used to calculate the velocity of a fluid in a pipe?
-Certainly. If you know the cross-sectional area and the velocity at one point in a pipe, you can calculate the velocity at another point using the equation A1V1 = A2V2, where A1 and V1 are the area and velocity at the first point, and A2 and V2 are the area and velocity at the second point.
What is a PHET simulation, and how does it relate to the continuity equation?
-A PHET simulation is an interactive educational tool that helps visualize and understand scientific concepts. In the context of the script, it is used to demonstrate how changes in the cross-sectional area of a pipe affect the velocity of the fluid, illustrating the principles of the continuity equation.
How can you calculate the cross-sectional area of a pipe or hose using its diameter?
-The cross-sectional area of a pipe or hose can be calculated using the formula A = πr^2, where r is the radius of the pipe or hose, and the radius is half of the diameter (r = diameter/2).
What is the significance of the continuity equation in practical applications such as firefighting?
-The continuity equation is significant in firefighting because it helps predict and control the behavior of water flowing through a fire hose. By understanding how changes in the hose's diameter or nozzle affect the water's velocity, firefighters can optimize the force and range of the water stream.
Can you provide an example calculation from the script where the continuity equation is used to find the velocity of water exiting a nozzle?
-In the script, an example is given where water flows through a fire hose with a diameter of 7.5 cm, and the velocity is 4.0 m/s. To find the velocity exiting a nozzle with a diameter of 2.3 cm, the continuity equation A1V1 = A2V2 is used. After calculating the areas using the formula for the area of a circle (πr^2) and converting units, the script finds the exit velocity (V2) to be around 43 m/s.
What is the practical implication of the velocity of water increasing as it exits a nozzle in a fire hose?
-The practical implication of the increased velocity of water exiting a nozzle is that it can provide a more powerful and focused stream, which is crucial for reaching greater distances and effectively combating fires.
Outlines
💧 Continuity Equation in Fluid Dynamics
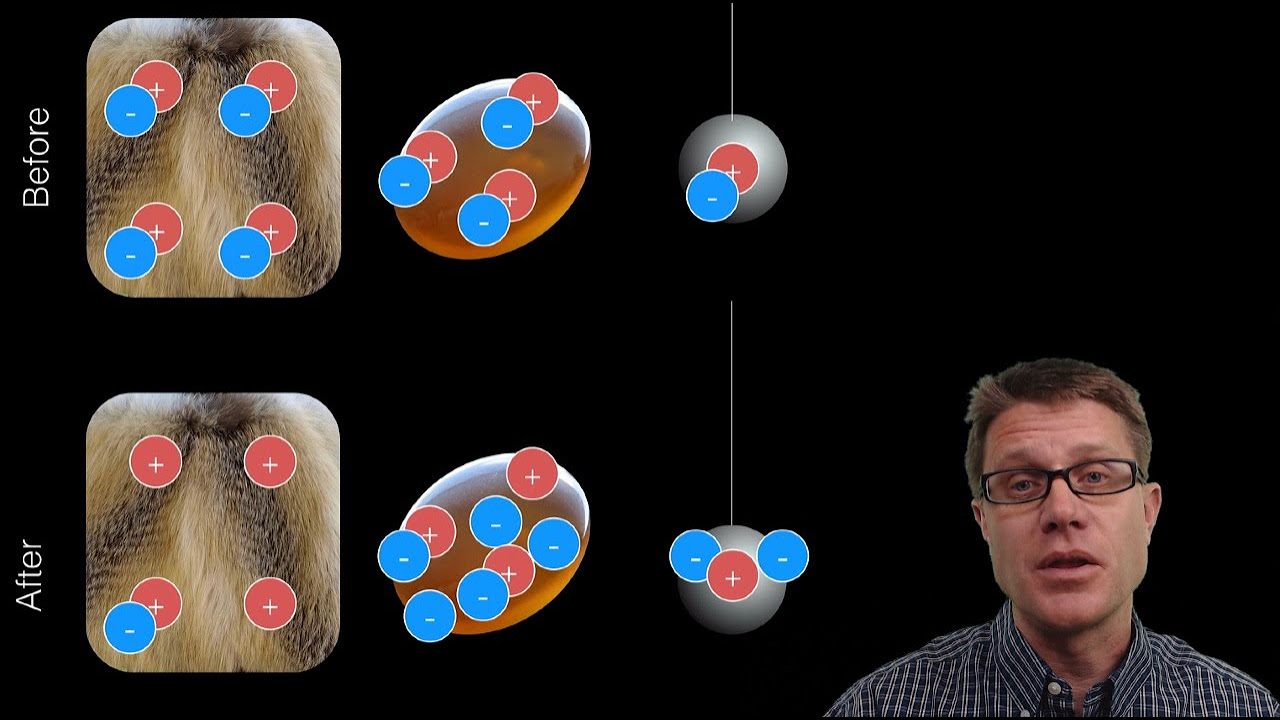
This paragraph introduces the concept of the continuity equation in fluid dynamics, which is an application of the conservation of mass principle. It uses the example of a fire hose to illustrate how the mass flow rate remains constant even when the hose's diameter changes. The equation is presented in terms of mass flow rate, involving the density, cross-sectional area, and velocity of the fluid. The paragraph explains that the density of water, for example, remains consistent through a pipe, leading to the equation being simplified to the product of cross-sectional area and velocity. The concept is further clarified through a simulation, showing how a decrease in area results in an increase in velocity, maintaining the product of area and velocity constant.
Mindmap
Keywords
💡Continuity Equation
💡Conservation of Mass
💡Fire Hose
💡Nozzle
💡Mass Flow Rate
💡Volumetric Flow Rate
💡Cross-Sectional Area
💡Velocity
💡Density
💡Flux Meter
💡Geometry
💡PhET Simulation
Highlights
The continuity equation is an application of the conservation of mass in fluids.
Mass flow rate in a fire hose is equal to the mass flow rate out, regardless of changes in diameter or nozzle size.
Restricting the area of a fluid flow increases its velocity according to the continuity equation.
The continuity equation can be represented by mass flow rate or volume flow rate.
The mass flow rate equation includes fluid density, cross-sectional area, and velocity.
Volume flow rate is often used when fluid density remains constant, simplifying the equation.
An example demonstrates how decreasing the cross-sectional area increases the velocity.
A PHET simulation illustrates the principle that A1V1 = A2V2.
Measuring the cross-sectional area and velocity at one point allows calculation at any other point with consistent fluid density.
A practical example involves calculating the velocity of water flowing through a fire hose with a restricted nozzle.
The continuity equation A1V1 = A2V2 is used to solve for unknown velocities.
Geometry is applied to calculate the cross-sectional area from the diameter of the hose and nozzle.
Conversion from centimeters to meters is necessary for accurate calculations.
The radius of the hose and nozzle is half of their respective diameters.
An example calculation shows a velocity increase from 4 m/s to approximately 43 m/s when the nozzle size is reduced.
The final velocity out of the nozzle is significantly higher than the initial velocity in the hose.
The video aims to teach viewers how to make flow calculations based on the continuity equation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: