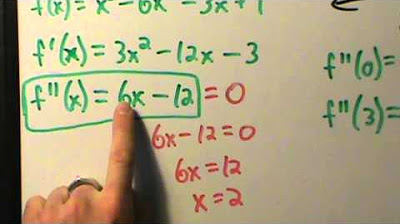Calculus I: Finding Intervals of Concavity and Inflection point

Rajendra Dahal
31 Dec 201904:21
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the use of calculus to determine the concavity and inflection points of the function f(x) = 2x^3 - 3x^2. The process involves finding the first and second derivatives of the function. The first derivative is found to be 6x^2 - 6x, and the second derivative is 12x - 6. By setting the second derivative to zero, a potential inflection point at x = 1/2 is identified. The function's concavity is then tested by plugging in values from intervals around the potential inflection point. It is determined that the function is concave upward for x > 1/2 and concave downward for x < 1/2. The inflection point is confirmed at (1/2, -1/2) after evaluating the function at x = 1/2. This comprehensive approach to using calculus to analyze the function's behavior is both educational and engaging for viewers interested in mathematical analysis.

Takeaways
  • 📚 The task involves analyzing a mathematical function using calculus to determine concavity and inflection points.
  • 🔍 The given function is 2x^3 - 3x^2.
  • 📉 Concavity is related to the second derivative of a function.
  • 📚 The first derivative of the function is 6x^2 - 6x.
  • 📈 The second derivative, crucial for concavity, is 12x - 6.
  • 🔍 Setting the second derivative to zero gives 12x - 6 = 0, which simplifies to x = 1/2.
  • 📝 An interval test is conducted using the second derivative to determine concavity.
  • 📉 The function is concave upward on (1/2, ∞) and concave downward on (-∞, 1/2).
  • 📍 The inflection point is where the concavity changes, which occurs at x = 1/2.
  • 📌 The inflection point's coordinates are found by evaluating the function at x = 1/2, resulting in the point (1/2, -1/2).
Q & A

  • What is the given function in the transcript?

    -The given function is 2x^3 - 3x^2.

  • What does concavity in calculus represent?

    -Concavity represents the curvature of a function, indicating whether the function bends upward (concave up) or downward (concave down).

  • How is concavity related to derivatives?

    -Concavity is related to the second derivative of a function. If the second derivative is positive, the function is concave up, and if it's negative, the function is concave down.

  • What is the first derivative of the given function?

    -The first derivative of the function 2x^3 - 3x^2 is 6x^2 - 6x.

  • What is the second derivative of the given function?

    -The second derivative of the function is 12x - 6.

  • How do you find the inflection point(s) of a function?

    -To find the inflection point(s), you set the second derivative equal to zero and solve for x. Then you check the intervals around the critical points to determine where the concavity changes.

  • What is the x-coordinate of the possible inflection point found in the transcript?

    -The x-coordinate of the possible inflection point is 1/2.

  • How did the transcript determine the intervals of concavity?

    -The transcript determined the intervals of concavity by plugging in test points from intervals around the critical point (x = 1/2) into the second derivative and observing the sign changes.

  • What are the intervals on which the given function is concave up or concave down?

    -The function is concave up on the interval (1/2, ∞) and concave down on the interval (-∞, 1/2).

  • What is the inflection point of the function?

    -The inflection point of the function is at x = 1/2, with the corresponding y-coordinate being -1/2 after evaluating the function at x = 1/2.

  • Why is it important to evaluate the function at the inflection point?

    -Evaluating the function at the inflection point gives you the exact coordinates of the point where the concavity changes, which is necessary for a complete description of the function's behavior.

  • Why is the function considered an even function in the transcript?

    -The function is considered even because it is symmetric about the y-axis, which can be inferred from the absence of an x term with an odd exponent in the polynomial.

Outlines
00:00
📚 Calculus Application: Finding Concavity and Inflection Points

The script introduces a mathematical problem involving a function, 2x^3 - 3x^2, and aims to determine its concavity and inflection points using calculus. It emphasizes that graphing is not sufficient and instead requires finding derivatives. The first derivative of the function is calculated as 6x^2 - 6x, and the second derivative is found to be 12x - 6. The second derivative is set to zero to find potential inflection points, resulting in x = 1/2. An interval test is conducted by plugging in test points into the second derivative to determine the concavity on either side of x = 1/2. The function is found to be concave upward on the interval (1/2, ∞) and concave downward on the interval (-∞, 1/2). The inflection point is identified at x = 1/2, and the corresponding y-coordinate is calculated by substituting x = 1/2 back into the original function, yielding the point (1/2, -1/2).

Mindmap
Keywords
💡Concavity
Concavity refers to the curvature of a function. In the context of the video, concavity is used to describe whether the function is bending upwards or downwards. The script discusses concavity in relation to the second derivative of the function, which indicates whether the function is concave up (positive second derivative) or concave down (negative second derivative). The video uses the second derivative test to find intervals of concavity.
💡Inflection Point
An inflection point is a point on the graph of a function where the concavity changes. The video script explains that the concavity changes from concave down to concave up at the point where the second derivative crosses zero. The script identifies the inflection point by setting the second derivative to zero and solving for x, finding it to be at x = 1/2.
💡Derivative
A derivative in calculus represents the rate of change of a function. The first derivative of the given function is calculated to find the slope of the tangent line at any point on the curve. The script mentions finding the first derivative of the function 2x^3 - 3x^2, which is 6x^2 - 6x, to analyze the function's concavity.
💡Second Derivative
The second derivative is the derivative of the first derivative and provides information about the concavity of a function. The script emphasizes the importance of the second derivative in determining the intervals of concavity and in finding the inflection point. For the given function, the second derivative is 12x - 6.
💡Interval Test
The interval test is a method used to determine the sign of the second derivative over different intervals. The script describes using the interval test by choosing test points from each interval and plugging them into the second derivative to see if it results in a positive or negative value, which helps in determining the concavity.
💡Polynomial Function
A polynomial function is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The video's function, 2x^3 - 3x^2, is a polynomial, and the script discusses its properties, such as being defined everywhere from negative infinity to positive infinity.
💡Function Evaluation
Function evaluation involves substituting a specific value into a function to find the corresponding output. In the script, after determining the x-coordinate of the inflection point to be 1/2, the function is evaluated at this point to find the y-coordinate, which is necessary to identify the exact inflection point.
💡Graphing
Graphing is the process of plotting the graph of a mathematical function or relation. The script initially mentions that the function cannot be graphed on a calculator to answer the question, implying that calculus methods are required instead of graphical analysis.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. The script uses calculus, specifically derivatives, to analyze the concavity and find the inflection points of the given function without resorting to graphical methods.
💡Rate of Change
The rate of change is a fundamental concept in calculus that describes how one quantity changes in relation to another. The first derivative of the function represents its rate of change. The script uses the first derivative to find the slope of the tangent line to the curve at any given point.
💡Even Function
An even function is symmetric with respect to the y-axis, meaning that f(x) = f(-x) for all x in the domain. The script mentions that the given function is an even function, which is a characteristic that can be inferred from its form and symmetry.
Highlights

The function to consider is 2x^3 - 3x^2.

The task is to find intervals of concavity and inflection points using calculus.

Concavity is related to the second derivative of the function.

The first derivative of the function is 6x^2 - 6x.

The second derivative is 12x - 6.

Setting the second derivative to zero gives x = 1/2 as a potential inflection point.

Interval testing is performed by considering the polynomial's behavior across intervals.

The function is defined for all real numbers from negative infinity to positive infinity.

The second derivative is tested at x = 0 and x = 1 to determine concavity.

When the second derivative is negative, the function is concave downward.

When the second derivative is positive, the function is concave upward.

The function is concave upward on the interval (1/2, positive infinity).

The function is concave downward on the interval (negative infinity, 1/2).

The inflection point occurs where concavity changes, identified at x = 1/2.

The inflection point's coordinates are found by evaluating the function at x = 1/2.

The inflection point is (1/2, -1/2).

Transcripts

Browse More Related Video

Finding Concavity and Inflection Points

Calculus I - Concavity and Inflection Points - Example 1

Increasing/Decreasing, Concave Up/Down, Inflection Points

Maxima , minima and point of inflection

Fiding Relative Max, Min and Inflection Point with Derivatives F4

Inflection Point Grade 12

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusConcavityInflection PointsDerivativesPolynomialGraphingFunction AnalysisMathematicsEducationalTutorial