Calculus 2 Lecture 6.5: Calculus of Inverse Trigonometric Functions
TLDRThis educational video script delves into the concept and application of inverse trigonometric functions, focusing on their derivatives and integrals. The instructor begins by explaining the necessity of functions being one-to-one to have inverses, using the domain restriction technique to make trigonometric functions invertible. The script proceeds to define the domains and ranges of inverse sine, cosine, and tangent functions, illustrating their graphs and properties. It also covers the process of finding derivatives of inverse trig functions using the chain rule and implicit differentiation, providing proofs for certain derivatives. The session includes practical examples and exercises to solidify understanding. Towards the end, the instructor introduces integrals involving inverse trig functions, demonstrating common integration techniques and the importance of substitutions to fit the integration table. The script is packed with interactive elements, ensuring a comprehensive grasp of the subject.
Takeaways
- 📚 The lesson focuses on inverse trigonometric functions, their meanings, graphs, domains, and ranges, as well as how to take their derivatives and integrals.
- 🔍 To find an inverse function, the original function must be one-to-one, which can be achieved by restricting the domain of trigonometric functions.
- 📉 The domains of inverse trig functions are specific and limited due to the restriction of the original trigonometric functions' domains to make them one-to-one.
- 🤔 The process of finding an inverse involves switching the roles of x and y, which means the domain and range of the original function become the range and domain of the inverse, respectively.
- 📈 Examples are given to illustrate how to determine the domain and range of inverse trig functions, such as sin^(-1), cos^(-1), and tan^(-1), by considering the restricted domains where the original functions are one-to-one.
- 👉 The importance of understanding the relationship between the original trigonometric functions and their inverses is emphasized for evaluating expressions and solving problems.
- 🧩 The concept of using a unit circle and triangles is introduced to help visualize and calculate values for inverse trigonometric functions, especially when dealing with angles and side lengths.
- ✏️ The script provides a step-by-step approach to differentiate inverse trig functions using the chain rule and the derivatives of the inverse functions, which are distinct from the derivatives of their original counterparts.
- 📝 The derivatives of inverse trig functions are presented as formulas that should be memorized and applied, as they involve the chain rule and are not intuitive like the derivatives of standard trigonometric functions.
- 🔁 The script demonstrates how to work with composite functions involving inverse trig functions, emphasizing the need to ensure the argument of the inner function is within its domain.
- 📚 The lesson concludes with proofs for some of the derivatives of inverse trig functions, showing the mathematical reasoning behind the formulas and their derivations.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is inverse trigonometric functions, including understanding what they are, their properties, domains, ranges, and how to find their derivatives and integrals.
Why do trigonometric functions need to be restricted to certain domains to have inverses?
-Trigonometric functions need to be restricted to certain domains to ensure they are one-to-one, which is a requirement for a function to have an inverse. Restricting the domain allows for the creation of a unique inverse function.
What is the process of finding the inverse of a trigonometric function?
-The process involves identifying a section of the trigonometric function that is one-to-one, restricting the domain if necessary, and then switching the roles of the x and y variables, effectively swapping the domain and range to find the inverse function.
What is the domain of the sine inverse function?
-The domain of the sine inverse function is from -1 to 1, inclusive. This is because the sine function can only output values between -1 and 1, and these become the input values for the inverse sine function.
How does the range of a trigonometric function become the domain of its inverse?
-When finding the inverse of a function, the roles of the x and y variables are switched. Therefore, the range of the original trigonometric function, which represents the set of possible output values, becomes the domain of the inverse function, representing the set of valid input values.
What is the relationship between the domain and range of the original function and its inverse when dealing with inverse trigonometric functions?
-For inverse trigonometric functions, the domain of the original function becomes the range of the inverse function, and the range of the original function becomes the domain of the inverse function. This is due to the nature of inverse functions where inputs and outputs are interchanged.
What is the derivative of the sine inverse function with respect to x?
-The derivative of the sine inverse function with respect to x is (1 / the square root of (1 - x^2)) dx, where x is the variable inside the sine inverse function.
How does the proof of the derivative of the cosine inverse function relate to the Pythagorean identity?
-The proof of the derivative of the cosine inverse function uses the Pythagorean identity (sin^2(y) + cos^2(y) = 1) to express sin(y) in terms of cos(y), which then allows for the application of the chain rule and the derivation of the formula for the derivative of the cosine inverse function.
What is the integral of a function that can be written in the form of 1 over the square root of (1 - u^2)?
-The integral of a function in the form of 1 over the square root of (1 - u^2) is the sine inverse of u plus a constant of integration.
Why are substitutions often used when finding integrals of inverse trigonometric functions?
-Substitutions are often used when finding integrals of inverse trigonometric functions to simplify the integral and make it fit a recognizable form that can be solved using the integration table or other known integral formulas.
Outlines
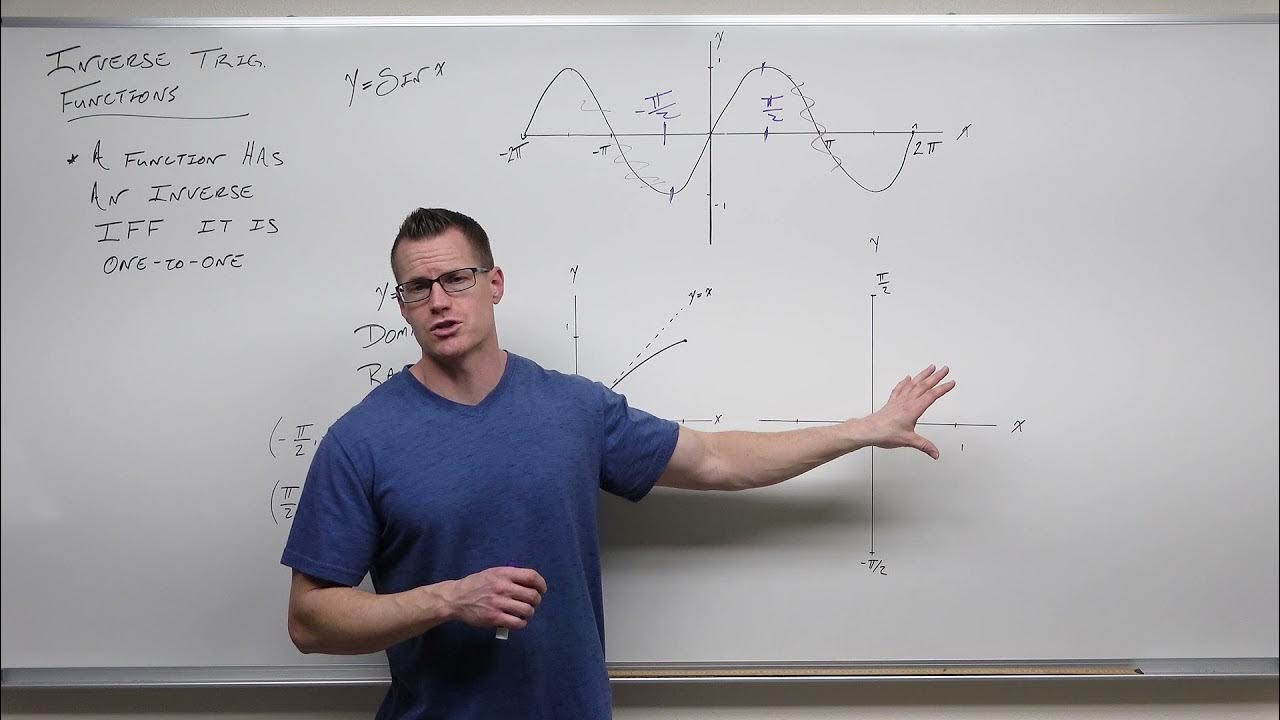
📚 Introduction to Inverse Trigonometric Functions
The lesson begins with an introduction to inverse trigonometric functions, focusing on their meaning, appearance, and the conditions under which they exist. The instructor emphasizes the importance of a function being one-to-one (1:1) to have an inverse. Trigonometric functions, such as sine and cosine, are discussed in terms of their domains and ranges, and how restricting the domain can create a 1:1 relationship, allowing for the existence of inverses. The concept of inverse functions is illustrated with the sine function, showing how restricting its domain to [π/2, 3π/2] makes it 1:1 and thus invertible.
🔍 Understanding Inverse Functions and Their Domains
This paragraph delves deeper into the concept of inverse functions, explaining how they switch the roles of x and y, effectively exchanging the domain and range of the original function. The instructor provides a detailed example using the sine function, illustrating how its inverse function is derived and highlighting the importance of the restricted domain for the inverse sine function to exist. The discussion includes the graphical representation of the sine function and its inverse, emphasizing the reflection across the line y=x.
📉 Trigonometric Functions and Their Inverses: Domain and Range
The instructor continues by discussing the domains and ranges of various trigonometric functions and their inverses, including sine, cosine, and tangent. For each function, a specific domain is chosen to ensure the function is one-to-one, allowing for the inverse to exist. The paragraph covers how to determine the domain and range of inverse functions by interchanging the x's and y's of the original function, and how the restricted domains lead to specific graphical representations for the inverses.
🤔 Evaluating Inverse Trigonometric Functions
This section focuses on how to evaluate inverse trigonometric functions, such as sin^(-1)(x), cos^(-1)(x), and tan^(-1)(x), by understanding their relationship with the original trigonometric functions. The instructor provides a step-by-step approach to finding the angles that correspond to given values of the inverse functions, using the unit circle and the restricted domains previously discussed. The importance of using a calculator for values not found on the unit circle is also mentioned.
📚 Derivatives of Inverse Trigonometric Functions
The lesson shifts to the topic of derivatives, starting with inverse trigonometric functions. The instructor presents the derivatives of sin^(-1)(x), cos^(-1)(x), and tan^(-1)(x), explaining that they differ from the derivatives of the original trigonometric functions. The focus is on understanding the application of the chain rule and the specific formulas associated with the derivatives of inverse functions.
🔍 Proofs of Derivatives for Inverse Trigonometric Functions
The instructor provides proofs for the derivatives of inverse trigonometric functions, such as cos^(-1)(x) and sec^(-1)(x), to demonstrate their derivation and the reasoning behind the formulas. The proofs involve implicit differentiation and the use of trigonometric identities, showcasing the mathematical process behind the derivation of these unique derivatives.
📉 Application of Chain Rule in Derivatives
This paragraph emphasizes the importance of the chain rule in calculating the derivatives of inverse trigonometric functions. The instructor illustrates how to apply the chain rule in various scenarios, including复合 functions, and how to correctly identify and substitute the inner function's derivative. The focus is on practicing the application of the chain rule to avoid common mistakes.
🤔 Advanced Derivatives and Integrals
The lesson continues with more complex examples of derivatives involving inverse trigonometric functions, such as the derivative of e^(x) * sec^(-1)(x). The instructor guides through the process of taking derivatives step by step, highlighting the importance of following the correct order of operations and the chain rule. The paragraph also introduces the concept of integrals involving inverse trigonometric functions.
📚 Integration of Inverse Trigonometric Functions
The instructor introduces new integrals for inverse trigonometric functions, explaining that only three new integrals are needed due to the negative relationships of the other three. The focus is on understanding how to integrate functions of the form 1/√(1-u^2), 1/√(1+u^2), and 1/(u^2+1), and how to apply substitutions to fit these forms.
🔍 Substitution in Integration
This section covers the technique of substitution in integration, particularly when dealing with inverse trigonometric functions. The instructor demonstrates how to manipulate the integral to fit the forms that can be integrated using the newly introduced integrals. The importance of recognizing patterns and applying substitutions effectively is emphasized.
📉 Complex Integration Examples
The lesson concludes with complex examples of integration, including functions with exponential and inverse trigonometric components. The instructor shows how to break down and simplify these integrals, using both substitution and the newly added integration formulas. The focus is on practicing these techniques to tackle more challenging integration problems.
Mindmap
Keywords
💡Inverse Trig Functions
💡Domain and Range
💡One-to-One Function
💡Horizontal Line Test
💡Implicit Differentiation
💡Chain Rule
💡Pythagorean Identity
💡Triangle Method
💡Arc Functions
💡Integration
Highlights
Introduction to inverse trigonometric functions, their meanings, and characteristics.
Explanation of the concept of inverse functions and the necessity for a function to be one-to-one to have an inverse.
Discussion on the domain restrictions of trigonometric functions to make them one-to-one for inverse function properties.
Illustration of the sine function's graph and its behavior to explain why domain restriction is necessary for inverse functions.
The process of finding the inverse of a restricted sine function and the resulting domain and range of the inverse sine function.
Understanding the relationship between the domain and range when switching from original trigonometric functions to their inverses.
Examples of finding inverse functions for sine, cosine, and tangent within specific domains.
Mistake made in the explanation of the cosine function's graph and its correction for clarity.
Derivation of the inverse cosine function, including its domain and range, and the graphical representation.
Explanation of the process to find the inverse tangent function and its properties.
Introduction to the inverses of cosecant and secant functions, their domains, and ranges.
The unique behavior of the inverse cotangent function and its domain and range.
Practical examples of evaluating inverse trigonometric functions using the unit circle and trigonometric identities.
Approaches to handle inverse trigonometric functions with calculators for values not found on the unit circle.
Compounding trigonometric relationships and methods to evaluate complex expressions involving inverse functions.
Proofs of derivatives of inverse trigonometric functions and the rationale behind their forms.
Application of the chain rule in finding derivatives of composite functions involving inverse trigonometric functions.
Integration of functions involving inverse trigonometric functions using substitution and manipulation to fit the integration table.
Transcripts
Browse More Related Video

Take Derivatives of Inverse Trig Functions (ArcSin, ArcCos) - [2]
Introduction to Inverse Trigonometric Functions (Precalculus - Trigonometry 17)

Inverse Trig Functions and Differentiation
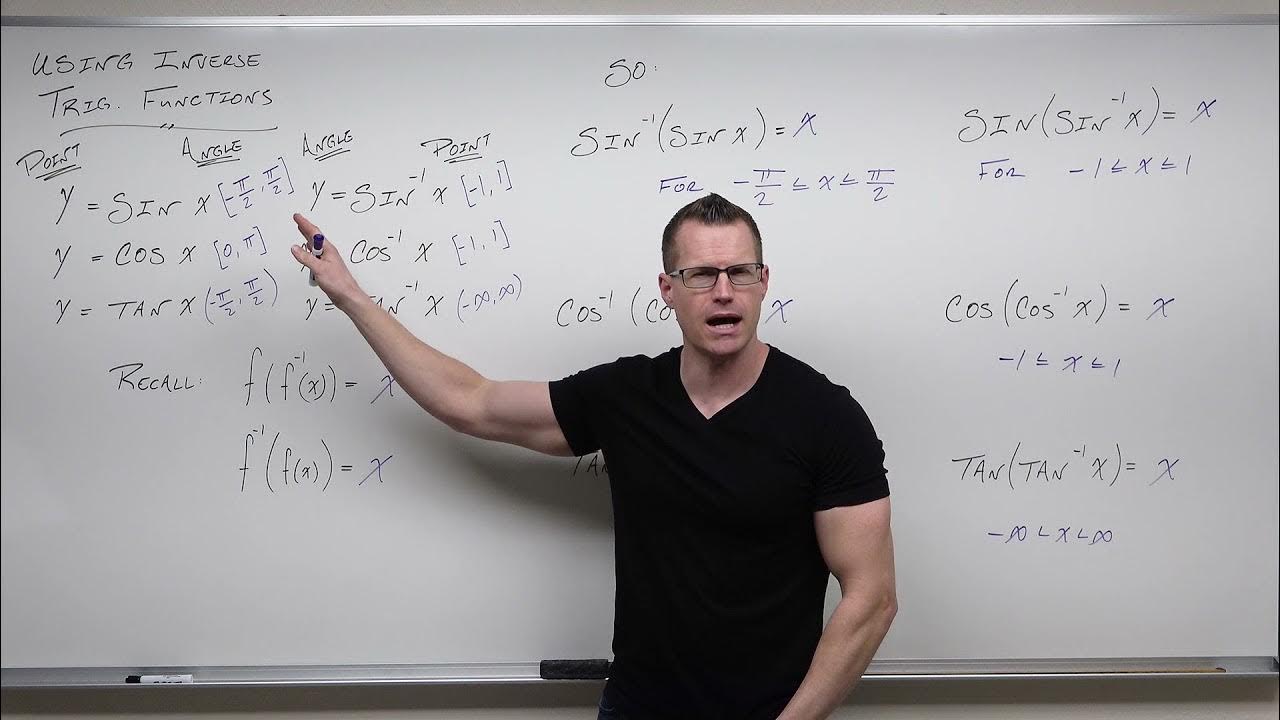
How to Use Inverse Trigonometric Functions (Precalculus - Trigonometry 18)

Natural Log Function Integration

Derivative of Inverse Trig Functions via Implicit Differentiation
5.0 / 5 (0 votes)
Thanks for rating: