Take Derivatives of Inverse Trig Functions (ArcSin, ArcCos) - [2]
TLDRThis advanced calculus tutorial focuses on the derivatives and integrals of inverse trigonometric functions. The instructor introduces the derivatives of arcsine, arccosine, arctangent, and their reciprocal functions, emphasizing their symmetry and simplicity due to specific range choices. The video demonstrates how to apply these derivatives using the chain rule and how they naturally lead to integrals of complex functions. Examples include finding derivatives of functions involving inverse trigonometric functions and evaluating definite integrals that result in inverse trigonometric expressions. The tutorial aims to equip viewers with the skills to tackle calculus problems involving these functions, highlighting the importance of understanding the unit circle and the ranges of the functions.
Takeaways
- 📚 The section focuses on the derivatives and integrals of inverse trigonometric functions, building upon the basics covered in the previous section.
- 🔍 Derivatives of inverse trig functions are presented as facts without derivation, emphasizing their application in problem-solving rather than their proof.
- 📉 The derivative of arcsine (sin^(-1)(x)) is 1/√(1-x^2), showcasing the symmetry with the derivative of arccosine (cos^(-1)(x)) being -1/√(1-x^2).
- 📈 The derivative of arctangent (tan^(-1)(x)) is 1/(1+x^2), with the inverse cotangent (cot^(-1)(x)) having a similar form but with a negative sign.
- 📊 The derivatives of inverse secant (sec^(-1)(x)) and inverse cosecant (csc^(-1)(x)) follow the same pattern, with 1/x√(x^2-1) and -1/x√(x^2-1) respectively.
- 🔑 The nice derivatives are attributed to the specific ranges chosen for the inverse trig functions, which simplify the expressions.
- ⚖️ Each inverse trig function has a corresponding integral, allowing for the integration of certain complex functions by recognizing their derivatives.
- 🔄 The chain rule is applied when differentiating functions involving inverse trig functions, such as tan^(-1)(x^3) or sin^(-1)(x^2).
- 📝 The process of evaluating definite integrals involving inverse trig functions requires understanding of the unit circle and the ranges of trig functions.
- 🧩 The video script also covers the technique of substitution to simplify integrals, as demonstrated with an integral involving x^2/√(1-x^6).
- 📉 The integral of 1/√(1-x^2) dx is shown to be the arcsine function, highlighting the direct relationship between the derivative and the integral of inverse trig functions.
Q & A
What is the main focus of this section of the Advanced Calculus 2 tutorial?
-The main focus of this section is to discuss the derivatives and integrals of inverse trigonometric functions, building upon the basics covered in the previous section.
Why does the instructor choose not to derive the derivatives of inverse trig functions in this section?
-The instructor chooses not to derive the derivatives because students are expected to use these derivatives as facts, focusing more on how to apply them to solve problems rather than proving them.
What is the derivative of the inverse sine function with respect to x?
-The derivative of the inverse sine function with respect to x is 1 over the square root of (1 - x^2).
How is the derivative of the inverse cosine function related to the derivative of the inverse sine function?
-The derivative of the inverse cosine function is similar to the derivative of the inverse sine function, but with a negative sign in front, which is -1 over the square root of (1 - x^2).
What symmetry can be observed in the derivatives of the inverse tangent and inverse cotangent functions?
-The symmetry observed is that the derivative of the inverse tangent function is 1 over (1 + x^2), and the derivative of the inverse cotangent function is the negative of that, which is -1 over (1 + x^2).
What is the integral of 1 over the square root of (1 - x^2) dx?
-The integral of 1 over the square root of (1 - x^2) dx is equal to the inverse sine function or arc sine function of x plus a constant, due to the fundamental theorem of calculus.
How does the chain rule apply when finding the derivative of a function like f(x) = arctan(x^3)?
-The chain rule is applied by taking the derivative of the outer function (1 / (1 + x^2) for arctan) and multiplying it by the derivative of the inner function (3x^2 for x^3).
What is the process for evaluating the definite integral of 6 / (1 + x^2) from 1 to the square root of 3?
-The process involves recognizing the integral as an inverse tangent function, pulling the constant 6 outside the integral, and then evaluating the inverse tangent function at the upper and lower limits of integration, resulting in 6 times the difference of arctan(sqrt(3)) - arctan(1).
How does the instructor simplify the derivative of f(x) = arctan(x/a)?
-The instructor simplifies the derivative by factoring out the constant 'a' and then simplifying the expression by multiplying the numerator and denominator by 'a' to clear the fractions.
What substitution is used to simplify the integral of x^2 / sqrt(1 - x^6) dx?
-The substitution used is u = x^3, which simplifies the integral because the derivative of u with respect to x is 3x^2, allowing for a cancellation in the integral.
How does the instructor evaluate the integral of x^2 / sqrt(1 - x^6) dx after the substitution?
-After the substitution, the integral simplifies to 1/3 times the integral of 1 / sqrt(1 - u^2) du, which is recognized as the inverse sine function. The integral is then evaluated as one-third times the inverse sine of u plus a constant, and the substitution for u is plugged back in.
Outlines
📚 Introduction to Calculus of Inverse Trigonometric Functions
This section of the 'Advanced Calculus 2' tutorial focuses on the derivatives and integrals of inverse trigonometric functions. The instructor plans to define the derivatives of each inverse trig function and work through problems involving them. The session builds upon the basics of inverse functions covered in the previous section, including their existence and range of angles. The derivatives of inverse sine, cosine, tangent, cotangent, secant, and cosecant functions are introduced as formulas to be used rather than derived in detail, emphasizing application over proof. The instructor also explains that knowing these derivatives inherently defines the integrals of certain functions, allowing students to solve more complex problems.
🔍 Derivatives of Inverse Trigonometric Functions
The tutorial delves into the specifics of finding derivatives of functions involving inverse trigonometric operations. The instructor provides the derivative formulas for inverse sine, cosine, tangent, cotangent, secant, and cosecant functions, highlighting the symmetry in their forms. For instance, the derivative of the inverse sine function is given as 1 over the square root of (1 - x^2), while the inverse cosine derivative is the negative of that. The inverse tangent and cotangent derivatives are also presented, showcasing a similar pattern. The importance of the chosen ranges for these functions in creating these symmetrical and simple derivative forms is discussed. The session also covers how to use these derivatives to solve integral problems, with the integral of the derivative of an inverse function naturally leading back to the original inverse function plus a constant.
📝 Application of Derivatives in Solving Problems
This part of the script illustrates how to apply the derivatives of inverse trigonometric functions to solve calculus problems. The instructor uses the chain rule to find the derivatives of composite functions, such as the inverse tangent of x cubed and the inverse sine of x squared. The process involves taking the derivative of the outer function and then multiplying by the derivative of the inner function, as demonstrated through step-by-step calculations. The examples given help students understand how to manipulate and simplify expressions involving inverse trigonometric functions to find their derivatives, preparing them for solving problems on tests and further studies.
🧩 Solving Integrals with Inverse Trigonometric Functions
The script moves on to integrals, starting with a definite integral involving the inverse tangent function. The instructor demonstrates how to evaluate the integral by recognizing the form that matches the integral of the derivative of the inverse tangent function. The process involves pulling out constants and evaluating the inverse tangent function at the limits of integration. The importance of knowing the range of angles for the tangent function is emphasized, and the evaluation of the integral results in an expression involving the difference of two inverse tangent functions. This section highlights the connection between derivatives and integrals and the practical application of inverse trigonometric functions in integral calculus.
🔄 Substitution Method in Integrals of Inverse Trigonometric Functions
The instructor introduces a technique for solving more complex integrals involving inverse trigonometric functions by using substitution. An example is given where the integral of x squared over the square root of (1 - x to the sixth power) is simplified by letting u be x to the third power. This substitution transforms the integral into a simpler form that resembles the integral of the derivative of the inverse sine function. The process involves taking the derivative of u with respect to x, solving for dx, and then substituting back into the integral. The result is an expression involving the inverse sine of u, plus a constant, which is then evaluated in terms of the original variable x. This method showcases a strategic approach to tackling integrals that can be related to inverse trigonometric functions.
Mindmap
Keywords
💡Inverse Trigonometric Functions
💡Derivatives
💡Integrals
💡Chain Rule
💡Symmetry
💡Ranges of Angles
💡Substitution
💡Unit Circle
💡Definite Integral
💡Indefinite Integral
Highlights
Introduction to the section on inverse trigonometric functions in advanced calculus.
Focus on derivatives and integrals of inverse trig functions rather than their derivation.
Listing the derivatives of inverse sine, cosine, tangent, cotangent, secant, and cosecant functions.
The symmetry in derivatives of inverse sine and cosine functions.
Derivative of inverse tangent and cotangent functions and their relationship.
Derivatives of inverse secant and cosecant functions and their symmetrical properties.
Importance of the range of angles in defining the derivatives of inverse trig functions.
Corresponding integrals of inverse trig functions based on their derivatives.
How to find the derivative of a function involving inverse tangent of a variable raised to a power.
Application of the chain rule in differentiating inverse trig functions.
Differentiating inverse sine of a squared variable using the chain rule.
Simplifying derivatives of inverse trig functions with constants.
Evaluating definite integrals involving inverse tangent functions.
Using substitution to simplify complex integrals involving inverse trig functions.
Evaluating integrals by transforming them into known inverse trig function forms.
Practical approach to solving integrals using properties of inverse trig functions.
The necessity of understanding inverse trig function evaluation for integral solutions.
Final summary emphasizing the importance of practice with inverse trig functions in calculus.
Transcripts
Browse More Related Video

Lesson 2 - Derivatives Of Inverse Trig Functions (Calculus 2 Tutor)

Inverse Trig Functions and Differentiation
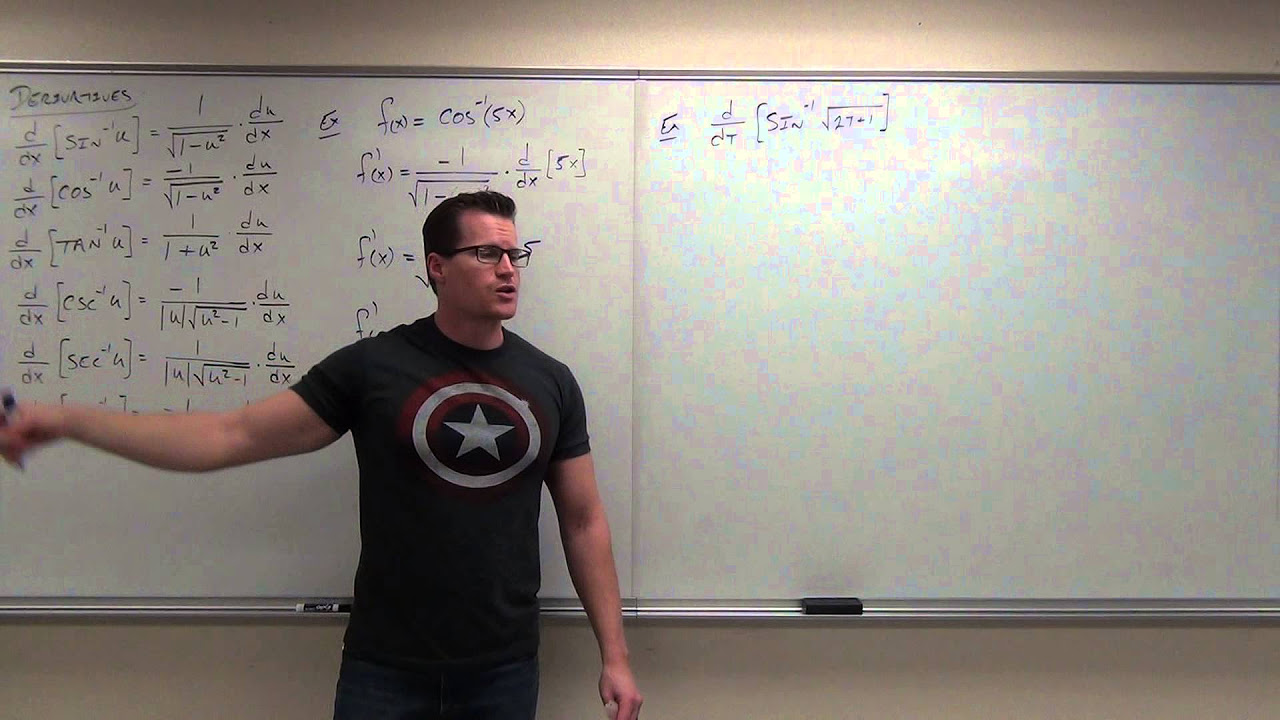
Calculus 2 Lecture 6.5: Calculus of Inverse Trigonometric Functions

Calculus - Find the derivative of inverse trigonometric functions

Derivatives of Inverse Trigonometric Functions

An Indepth Look at Using Inverse Trig Functions (Precalculus - Trigonometry 21)
5.0 / 5 (0 votes)
Thanks for rating: