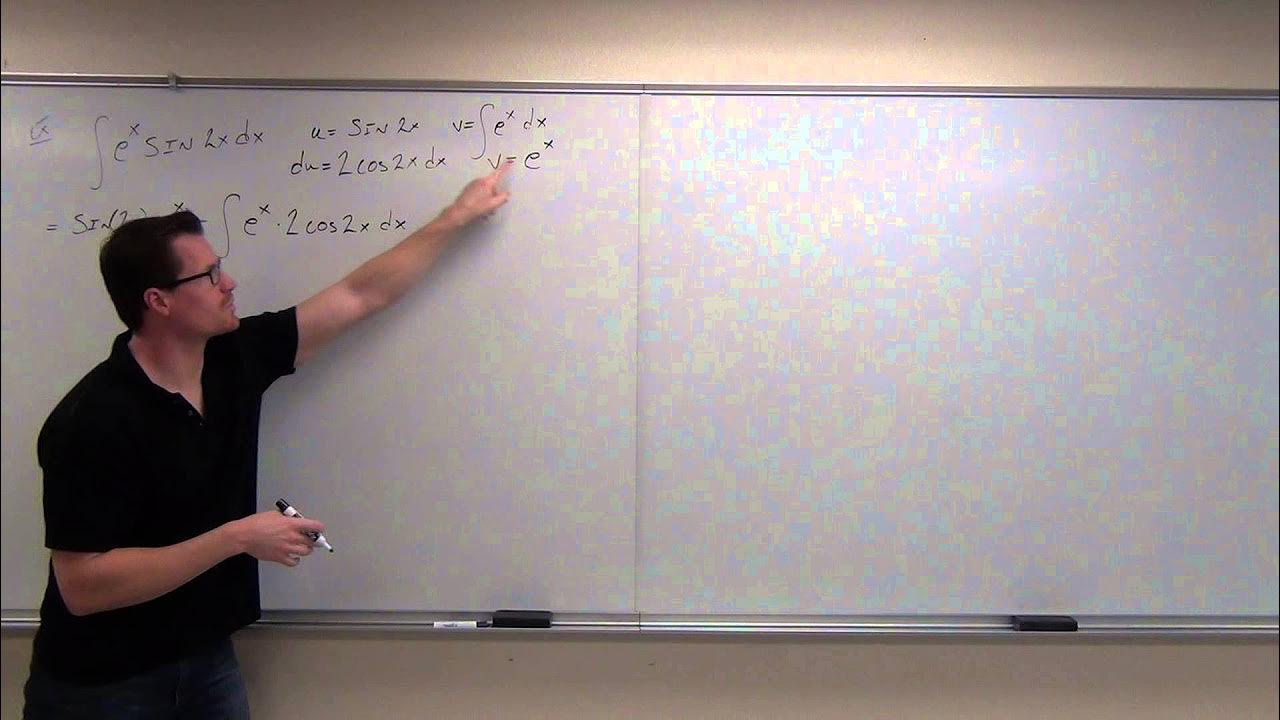What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2

blackpenredpen

19 Feb 201922:39

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video offers a unique approach to calculus, focusing on discussing integration techniques rather than solving integrals directly. Aimed at college students, it covers twelve integrals, emphasizing the importance of understanding integration by parts, partial fractions, and trigonometric identities. The presenter provides a downloadable file and encourages viewers to like and share the video. The script delves into specific integrals, such as natural log functions and trigonometric expressions, illustrating the thought process behind choosing the right method for each scenario. The video concludes with an invitation for feedback and a wish for a successful semester, highlighting the fun aspect of mastering integrations.

Takeaways

📚 The video is aimed at calculus students and covers a variety of integration techniques.
📈 The presenter introduces 12 different integrals and discusses the methods to solve them.
🔗 A downloadable file with the integrals is available for free, linked in the video description.
👍 The video encourages viewers to like and share the content with peers and teachers.
📝 Integration by parts is highlighted as a key technique for integrals involving natural logarithms and powers of x.
📉 The video demonstrates the use of trigonometric identities for integrals involving secant and tangent functions.
🤔 Partial fraction decomposition is explained as a method for integrating rational functions.
🔍 Substitution is suggested for integrals that can be simplified, such as those involving tangent or secant squared.
🧩 The process of integration by parts is broken down step by step for clarity.
🔄 Repeating integrals are shown with the use of integration by parts leading to a recursive solution.
📚 The video concludes with a reminder to show all work and to focus on the final answer for exams.

Q & A

What is the main focus of the video?
-The video focuses on discussing the techniques to be used for solving a set of integrals, rather than solving them directly.
Who is the target audience for this video?
-The video is intended for calculus students who are familiar with integration by parts, partial fractions, and trigonometric integral identities.
How many integrals are covered in the video?
-There are a total of twelve integrals discussed in the video.
What is the first integral discussed in the video?
-The first integral discussed is the integral of the natural log of X over X to the third power.
What technique is suggested for the integral of natural log of X over X to the third power?
-Integration by parts is suggested for this integral, as it involves both the natural log of X and a power of X.
What substitution is used for the integral of secant to the fourth power of X?
-The substitution involves expressing secant square X in terms of tangent, which simplifies the integral.
How is the integral of (2x + 3) / (x^2 - 5x + 4) approached?
-The integral is approached by factoring the denominator and using the method of partial fractions.
What is the process for finding the constants A and B in the partial fraction decomposition?
-The process involves plugging in values of X that make the denominator zero to solve for A and B.
What substitution is used for the integral of x^2 times tangent of X cubed?
-The substitution involves letting u equal x cubed, which simplifies the integral by reducing the power of X.
How is the integral of 1 over (1 + x^2) + (25/2)^power handled?
-The integral is simplified by recognizing it as a form of secant squared, which allows for a trigonometric identity to be applied.
What is the integral of e to the square root of x?
-The integral is approached by making a substitution where u equals the square root of x, which simplifies the integral to a form that can be solved using integration by parts.
What identity is used to simplify the integral of sine square X?
-The identity used is sine square X equals 1/2 - 1/2 cosine of 2X, which simplifies the integral.
How is the integral of 1 over square root of x plus 1 minus square root of x approached?
-The integral is approached by multiplying the numerator and denominator by the conjugate to eliminate the square roots in the denominator.
What technique is used for the integral of e to the x over secant X?
-Integration by parts is used for this integral, which leads to a repeating situation that requires careful handling.
How is the integral of 1 over (1 + cosine X) simplified?
-The integral is simplified by multiplying the numerator and denominator by the conjugate, which transforms it into a form involving sine squared X.
What is the approach for the integral of (X - 4) / (x^2 + 1/4 - 1)?
-The integral is approached by factoring the denominator and using partial fractions for the different linear and irreducible quadratic factors.
How is the integral of X / sqrt(1 - X^2) handled?
-The integral is handled by using a trigonometric substitution, where X is replaced with sine theta, and the differential DX is adjusted accordingly.
What is the final message of the video?
-The final message is to wish the viewers good luck with their integrations and to have a wonderful semester, emphasizing that integrations can be fun.

Outlines

00:00

📚 Introduction to Integration Techniques

The video begins with an introduction to various integration techniques suitable for calculus students. The speaker emphasizes the importance of knowing integration by parts, partial fractions, and trigonometric identities. A file containing twelve integrals is offered for download, and the audience is encouraged to like and share the video. The first integral discussed is the natural logarithm of X over X to the third power, which is approached using integration by parts.

05:00

🔢 Advanced Integration Examples

The video continues with a series of complex integration problems. The second problem involves integrating a function involving secant to the fourth power, which is simplified using trigonometric identities. The third problem is a rational function that is solved using partial fraction decomposition. The video also covers integration involving exponential and trigonometric functions, using substitution methods and recognizing patterns to simplify the process.

10:01

🧮 Integration by Parts and Trigonometric Identities

The video script delves into the application of integration by parts and trigonometric identities to solve specific integrals. It discusses the integration of e to the power of the square root of X by using substitution (u-substitution) and the integration by parts method. The process is explained step by step, highlighting the need to revert back to the original variable at the end of the integration.

15:01

📉 Integration of Trigonometric Powers

The video tackles the integration of sine squared X and other trigonometric functions. It covers the use of power reduction formulas and the strategy of multiplying by conjugates to eliminate square roots in the denominator. The speaker also discusses the integration of functions involving secant and cosecant, emphasizing the need to recognize patterns and use appropriate trigonometric identities.

20:03

🔁 Repeating Integration by Parts

The final paragraph focuses on a repeating situation in integration by parts, particularly with the integral of e to the power of X over secant X. The process is illustrated by differentiating and integrating the given functions, resulting in a pattern that can be simplified. The video concludes with encouragement for students to practice integration, noting that it can be an enjoyable aspect of calculus.

Mindmap

Keywords

💡Integration by Parts

Integration by Parts is a technique used in calculus to integrate products of functions. It is analogous to the product rule for differentiation. In the video, it is mentioned as a method for solving integrals of the form 'X to some power times natural log of X', where the integration by parts is applied to break down the integral into simpler, more manageable parts. An example given is the integral of the natural log of X over X to the third power.

💡Partial Fractions

Partial Fractions is a method used to integrate rational functions, particularly those that can be broken down into simpler fractions. The process involves factoring the denominator and expressing the integrand as a sum of simpler fractions, each of which can be integrated separately. In the script, partial fractions are used to integrate '2x + 3 over x squared minus 5x + 4' by factoring the denominator and setting up the integral in terms of simpler fractions.

💡Trig Integrals Identities

Trig Integrals Identities refer to the set of identities used to simplify the integration of trigonometric functions. These identities can transform complex trigonometric integrals into more straightforward forms that are easier to integrate. In the video, trig identities are used to simplify the integral of 'secant to the fourth power of X' by expressing it in terms of 'tangent square X plus one'.

💡Natural Logarithm

Natural Logarithm, often denoted as ln(x), is the logarithm to the base 'e', where 'e' is an irrational constant approximately equal to 2.71828. It is a fundamental concept in calculus and is used in various integration techniques. In the video, the natural log of X is part of the integral 'natural log of X over X to the third power', where the integration by parts is suggested as the method to solve it.

💡Conjugate

In the context of the video, the term 'conjugate' refers to the process of multiplying a binomial by its conjugate to eliminate square roots from the denominator, which simplifies the integration process. This technique is used when dealing with rational expressions involving square roots, as shown in the script when simplifying the integral '1 over square root of x plus 1 minus square root of x'.

💡Substitution

Substitution is a common technique in calculus used to transform the integral of a function into a different integral that is easier to solve. By setting a new variable equal to a part of the original function, the integral can be simplified. In the video, substitution is used in various contexts, such as letting 'u' equal to 'x cube' to simplify the integral of 'x squared times tangent of X'.

💡Di Method

The 'Di Method', also known as Integration by Parts, is a specific approach to integrating functions that are products of other functions. The method involves differentiating one part of the function and integrating the other part, then combining them in a systematic way. The video mentions setting up the integral by the 'Di' method, which is a shorthand for the integration by parts process.

💡Tangent and Secant

Tangent and Secant are trigonometric functions that are integral to solving certain types of integrals in calculus. The tangent function is the ratio of the opposite side to the adjacent side in a right-angled triangle, while the secant is the reciprocal of the cosine function. In the video, tangent and secant are used in the context of integrals, such as 'secant to the fourth power of X' and 'e to the x over secant X'.

💡Repeating Situation

A 'Repeating Situation' in integration refers to a scenario where the integration by parts must be applied multiple times due to the structure of the integral. This typically occurs when the derivative and integral of the function yield the same or a similar function, leading to a recursive pattern. The video describes a repeating situation when integrating 'e to the x times cosine X', where integration by parts must be applied iteratively.

💡Rational Function

A rational function is a function that is the ratio of two polynomials. In calculus, integrating rational functions can be complex and often requires techniques such as partial fraction decomposition or other simplification methods. The video discusses integrating rational functions, specifically mentioning the integral of '2x + 3 over x squared minus 5x + 4', which is a rational function.

💡Irreducible Quadratic

An 'Irreducible Quadratic' is a quadratic polynomial that cannot be factored into linear polynomials over the real numbers. In the context of integration, dealing with irreducible quadratics in the denominator often requires special techniques. The video script refers to an irreducible quadratic when discussing the integral of '1 over x squared plus 1', which is part of a larger rational function.

Highlights

The video discusses the use of integration techniques for calculus students, including integration by parts and partial fractions.

A file containing twelve integrals is available for download, free of charge, to aid in learning and practice.

The video introduces the concept of integration by parts for the integral of the natural log of X over X to the third power.

Trig identities are used to simplify the integral of secant to the fourth power, showcasing an alternative to integration by parts.

The technique of partial fractions is demonstrated for integrating a rational function with linear factors in the denominator.

A substitution method is applied to the integral of X cubed times tangent of X, simplifying the process.

The integral of e to the power of the square root of X is tackled by a substitution that transforms the expression into a more manageable form.

An identity for sine squared X is used to reduce the power and simplify the integral, highlighting the utility of trigonometric identities.

The video demonstrates how to eliminate square roots from a denominator by multiplying by a conjugate, simplifying the integral.

Integration by parts is used for the integral of e to the X times cosine X, leading to a repeating situation that simplifies the process.

The integral of 1 over 1 plus cosine X is simplified by multiplying by the conjugate, transforming it into a more recognizable form.

Partial fractions are used to integrate a function with an irreducible quadratic term in the denominator.

The video emphasizes the importance of noting the derivative of the integrand in the process of integration by parts.

The use of substitution is highlighted in the integral of X to the power of 1/4 minus one, transforming the square root into a more integrable form.

The video concludes by encouraging students to apply the techniques learned and to enjoy the process of integration as a fun challenge.

Transcripts

Browse More Related Video

Calculus 2 - Basic Integration

Calculus 2 Final Exam Review -

ALL OF Calculus 2 in a nutshell.

Lec 30 | MIT 18.01 Single Variable Calculus, Fall 2007

Calculus 2 Lecture 7.1: Integration By Parts

Trigonometric Integrals

Related Tags

Calculus Techniques Integration by Parts Trig Identities College Math Logarithmic Integrals Partial Fractions Trigonometric Integrals Integration Strategies Advanced Mathematics Math Tutorial Educational Content