Trigonometric Integrals

The Organic Chemistry Tutor

26 Mar 202131:28

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is a comprehensive guide to solving trigonometric integrals, focusing on the application of various trigonometric identities and power-reducing formulas. It walks through several problems, demonstrating techniques such as u-substitution and foiling to simplify expressions and find anti-derivatives. The script covers integrals of trigonometric functions raised to different powers, products of trigonometric functions, and the use of double angle formulas. The approach emphasizes the importance of recognizing patterns and choosing the most efficient method for each problem.

Takeaways

📚 Basic trigonometric identities are essential for integrating trigonometric expressions, such as sine squared plus cosine squared equals one.
🔄 Understanding power-reducing formulas is crucial, like sine squared can be reduced to one half of (1 - cosine of 2x).
🔧 The use of u-substitution is a common technique for solving integrals involving trigonometric functions, as demonstrated with cosine to the third power of x.
🌀 Mastery of double angle formulas is important for simplifying expressions, for example, sine of 2x can be expressed as 2sine x cosine x.
📈 The process of expanding and simplifying expressions using FOIL (First, Outer, Inner, Last) is demonstrated when integrating cosine to the fifth power of x times sine x.
🤝 The combination of trigonometric identities and power-reducing formulas is necessary for more complex integrals, such as the integral of sine to the fifth power of x times cosine squared x.
📌 When integrating products of trigonometric functions, like sine squared and cosine squared, it's beneficial to use the power-reducing formulas to simplify the expression first.
🧠 The concept of changing the angle in power-reducing formulas is highlighted, where the angle doubles with each successive application of the formula.
🛠️ The script demonstrates the importance of recognizing when to use sine or cosine in u-substitution to effectively cancel out terms and simplify the integral.
📊 The final answers to the integrals are provided in a structured form, showing the application of the discussed techniques and formulas.
🎓 The video script serves as a comprehensive guide to tackling a variety of trigonometric integrals, emphasizing the importance of practice and familiarity with formulas.

Q & A

What is the fundamental trigonometric identity for sine and cosine?
-The fundamental trigonometric identity is that sine squared plus cosine squared equals one.
What is the relationship between tangent squared and secant squared?
-One plus tangent squared is equal to secant squared.
What is the formula for cosine squared in terms of sine squared?
-Cosine squared can be expressed as one minus sine squared.
What are the three forms of the double angle formula for cosine?
-Cosine of double angle can be expressed as cosine squared minus sine squared, as one minus two sine squared, or as two cosine squared minus one.
How can sine squared be reduced using power reducing formulas?
-Sine squared can be reduced to one half times one minus cosine of double angle, or sine squared can be reduced to one half times one plus cosine of double angle.
What is the method used to find the antiderivative of cosine cubed?
-The method used is u-substitution, where cosine squared is replaced with one minus sine squared, and then u is substituted with sine x to find the antiderivative.
What is the antiderivative of cosine raised to the fifth power?
-The antiderivative is sine x minus two over three sine to the third power of x plus one over five sine to the fifth power of x plus a constant.
How is the problem of finding the indefinite integral of cosine to the fifth x times sine x approached?
-The problem is approached by making u equal to cosine, with du as negative sine x dx, and then using u-substitution to find the integral.
What is the strategy for finding the indefinite integral of sine to the fifth power times cosine squared x?
-The strategy is to make u equal to cosine, since cosine has an even power and allows for easier manipulation of the expression into terms involving only cosine, and then use u-substitution to solve the integral.
How does the power reducing formula for sine squared differ from that for cosine squared?
-The power reducing formula for sine squared is one half times one minus cosine of double angle, while for cosine squared it is one half times one plus cosine of double angle.
What is the antiderivative of sine squared x?
-The antiderivative is one half x minus one fourth sine of double angle x, divided by two, plus a constant.

Outlines

00:00

📚 Trigonometric Integrals and Formulas

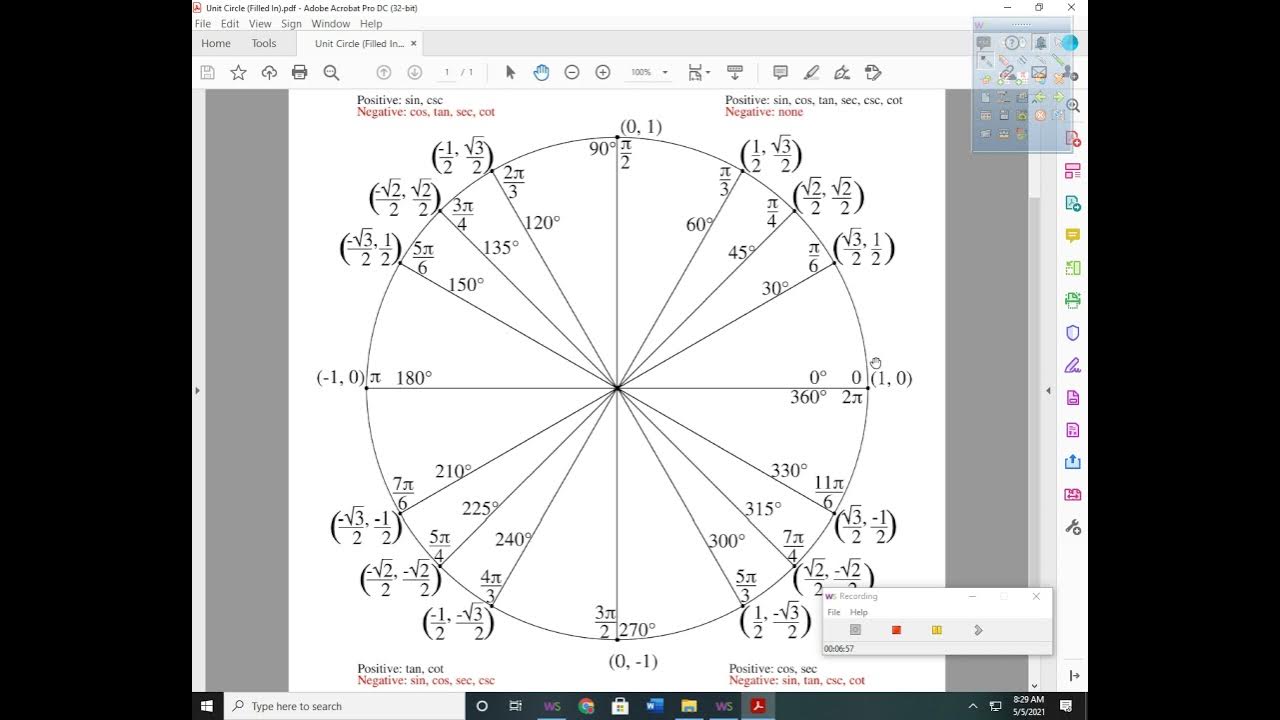
This paragraph introduces the topic of trigonometric integrals, emphasizing the importance of reviewing key formulas for successful integration. It starts with fundamental trigonometric identities such as sine squared plus cosine squared equals one and moves on to more complex formulas like one plus tangent squared equals secant squared. The paragraph also covers double angle formulas and power reducing formulas, providing a solid foundation for tackling trigonometric integrals.

05:01

🧠 Anti-Derivative of Trigonometric Functions

The focus of this paragraph is on finding the anti-derivatives of various trigonometric functions. It walks through the process of integrating cosine to the third power and cosine raised to the fifth power, using substitution and trigonometric identities. The paragraph also introduces the concept of u-substitution, where a variable is chosen to simplify the integral, and demonstrates its application in solving the given problems. The solutions are presented in a step-by-step manner, making it easier to understand the process.

10:03

🔢 Working with Sine and Cosine in Integrals

This paragraph delves into the integration of more complex trigonometric expressions involving both sine and cosine functions. It covers the integration of products of sine and cosine, as well as the use of power reducing formulas to simplify the integrals. The paragraph also discusses the choice of u in u-substitution, highlighting the importance of selecting the right variable for efficient problem-solving. The detailed explanation includes the steps to integrate sine to the fifth power times cosine squared and other similar problems.

15:04

📈 Sine Squared and Cosine Squared Integrals

This paragraph addresses the integration of sine squared and cosine squared functions, including their powers. It explains the use of power reducing formulas to simplify the integrals and the process of integrating these expressions. The paragraph provides a clear methodology for tackling these types of integrals, including the distribution of terms and the final simplification of the results. The explanation is thorough, ensuring a comprehensive understanding of the process.

20:07

🌀 Advanced Trigonometric Integrals

The paragraph presents advanced techniques for integrating more complex trigonometric expressions, such as sine squared cosine squared and cosine squared times tangent cubed. It introduces the concept of converting tangent to sine over cosine and the use of power reducing formulas to handle higher powers. The paragraph also discusses the strategy of choosing the appropriate u for u-substitution, ensuring the efficient cancellation of terms. The detailed walkthrough of the integration process helps to clarify the steps involved in solving these challenging problems.

25:09

📊 Solving Trigonometric Integrals with U-Substitution

This final paragraph of the script focuses on the application of u-substitution in solving trigonometric integrals. It provides a step-by-step guide on how to handle integrals involving sine and cosine functions, including the transformation of expressions and the selection of the correct u variable. The paragraph concludes with the solution of the integral of cosine squared times tangent to the third power, demonstrating the successful use of the techniques discussed throughout the video.

Mindmap

Keywords

💡Trigonometric Integrals

Trigonometric Integrals are a type of integral in calculus that involve trigonometric functions. In the context of the video, these integrals are the focus, and the viewer is encouraged to review formulas related to trigonometric functions to better understand the integration process. The video provides several examples of how to solve these integrals using various techniques such as substitution and power reducing formulas.

💡Trigonometric Identities

Trigonometric Identities are equations that are true for all values of the variables involved. They are essential tools in simplifying trigonometric expressions and solving trigonometric integrals. The video mentions several identities, such as sine squared plus cosine squared equals one and one plus tangent squared equals secant squared, which are used to transform complex expressions into simpler forms for integration.

💡U-Substitution

U-Substitution is a technique used in calculus to evaluate integrals by introducing a new variable (u) in place of the original variable (x). This method is particularly useful when the integrand can be expressed in terms of a function of u and its derivative. In the video, u-substitution is applied multiple times to simplify and solve trigonometric integrals, such as the integral of cosine cubed and cosine raised to the fifth power.

💡Power Reducing Formulas

Power Reducing Formulas are used to simplify the integral of trigonometric functions by reducing the power of the function to a form that is easier to integrate. These formulas are particularly helpful when dealing with trigonometric functions raised to high powers. In the video, power reducing formulas for sine and cosine squared are introduced and used to simplify integrals, such as sine squared reduced to one half times one minus cosine of two x.

💡Double Angle Formulas

Double Angle Formulas relate the trigonometric functions of an angle to the functions of twice that angle. They are crucial for simplifying expressions involving trigonometric functions and are used in the integration process. The video discusses double angle formulas for sine and cosine, such as sine two x being equal to two sine x times cosine x, and how they can be rearranged into different forms to facilitate integration.

💡Anti-Derivative

The Anti-Derivative, also known as the Indefinite Integral, is the function that represents the area under the curve of the original function up to a constant. In the context of the video, finding the anti-derivative is the primary goal, as it is the process of reversing the differentiation to find the original function. The video demonstrates how to find the anti-derivatives of various trigonometric expressions using different techniques.

💡Integration

Integration is a fundamental process in calculus that involves finding the area under a curve or the anti-derivative of a given function. It is the reverse operation of differentiation. The video focuses on the integration of trigonometric functions and uses various techniques such as u-substitution and power reducing formulas to evaluate integrals.

💡Sine and Cosine Functions

Sine and Cosine Functions are the two primary trigonometric functions that describe periodic phenomena such as the motion of waves and the position of the Earth in its orbit. They are used extensively in the video to demonstrate the integration of trigonometric expressions and the application of various formulas and techniques.

💡Tangent and Cotangent Functions

Tangent and Cotangent Functions are trigonometric functions that relate the ratio of the opposite side to the adjacent side in a right triangle. The Tangent function is the ratio of sine to cosine, while the Cotangent is the reciprocal of the tangent. These functions are used in the video to illustrate the integration process, particularly when dealing with expressions that involve the tangent function, such as the integral of cosine squared times tangent to the third power.

💡Foil Method

The Foil Method is a technique used to expand the product of two binomials. It stands for 'First, Outer, Inner, Last,' referring to the terms that are multiplied in each step of the expansion. This method is not explicitly mentioned in the video but is relevant when expanding expressions like (1 - u^2)(1 - u^2) during the integration process.

Highlights

Review of trigonometric formulas for integration, including sine squared plus cosine squared equals one.

Introduction of the formula one plus tangent squared equals secant squared.

Explanation of the formula one plus cotangent squared equals cosecant squared.

Double angle formulas for sine and cosine, including sine two x equals two sine x cosine x.

Power reducing formulas for sine and cosine squared, such as sine squared reduced to one half times one minus cosine two x.

Anti-derivative of cosine to the third power using u-substitution and trigonometric identities.

Integration of cosine raised to the fifth power using u-substitution and power reduction.

Integration of cosine to the fifth x times sine x using u-substitution and simplification.

Integration of sine to the fifth power times cosine squared x using u-substitution and trigonometric identities.

Integration of sine to the fifth power of x times cosine cube x using power reduction and u-substitution.

Integration of sine squared x using power reducing formulas and double angle identities.

Integration of cosine squared 3x using power reducing formulas and substitution.

Integration of sine to the fourth x using power reducing formulas and double angle identities.

Integration of sine squared x times cosine squared x using power reducing formulas and substitution.

Integration of sine squared x times cosine squared x using power reducing formulas and substitution, with a focus on simplifying the expression.

Integration of cosine squared x times tangent to the third power using substitution and simplification.

Final answer for the indefinite integral of cosine squared x times tangent to the third power, involving natural logarithm and cosine squared.

Transcripts

Browse More Related Video

5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Integration of Rational Functions By Completing The Square - Calculus

Indefinite Integral - Basic Integration Rules, Problems, Formulas, Trig Functions, Calculus

Lec 27 | MIT 18.01 Single Variable Calculus, Fall 2007

Calculus 2 - Basic Integration

How to Use the Double and Half Angle Formulas for Trigonometry (Precalculus - Trigonometry 28)

Related Tags

Trigonometry Integrals Mathematics u-Substitution Power Reducing Formulas Trig Identities Educational Advanced Math Calculus