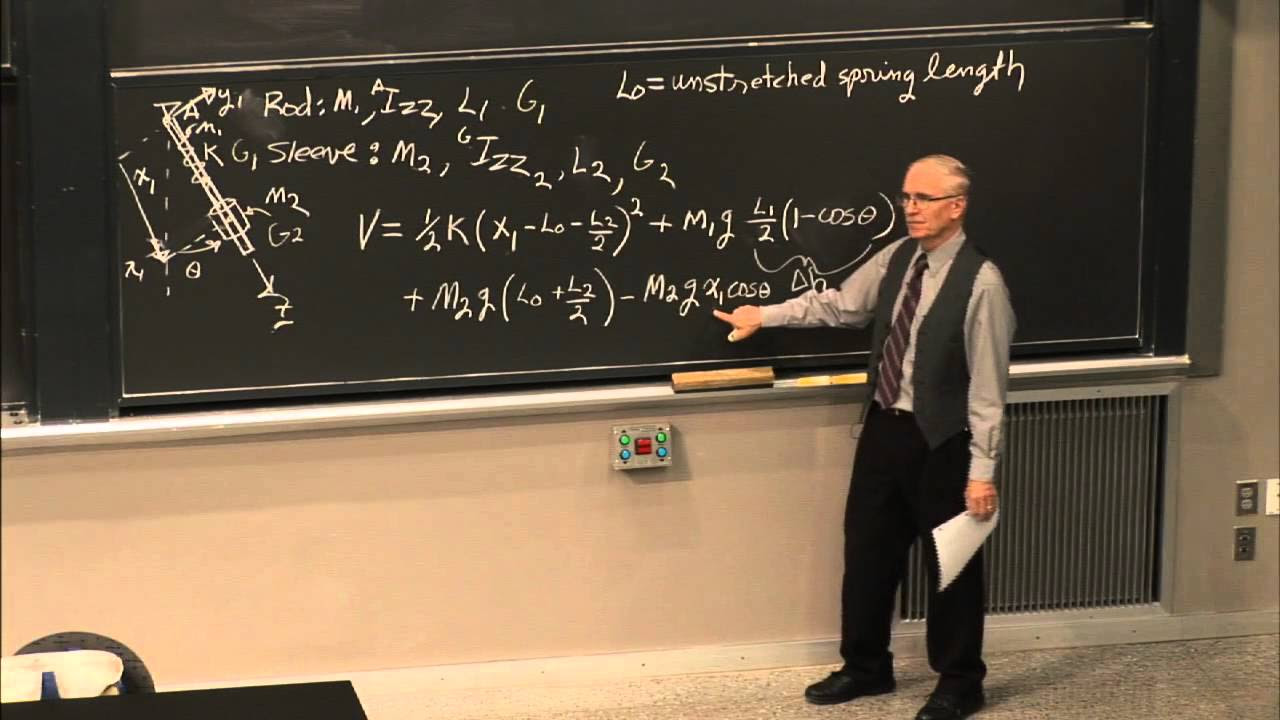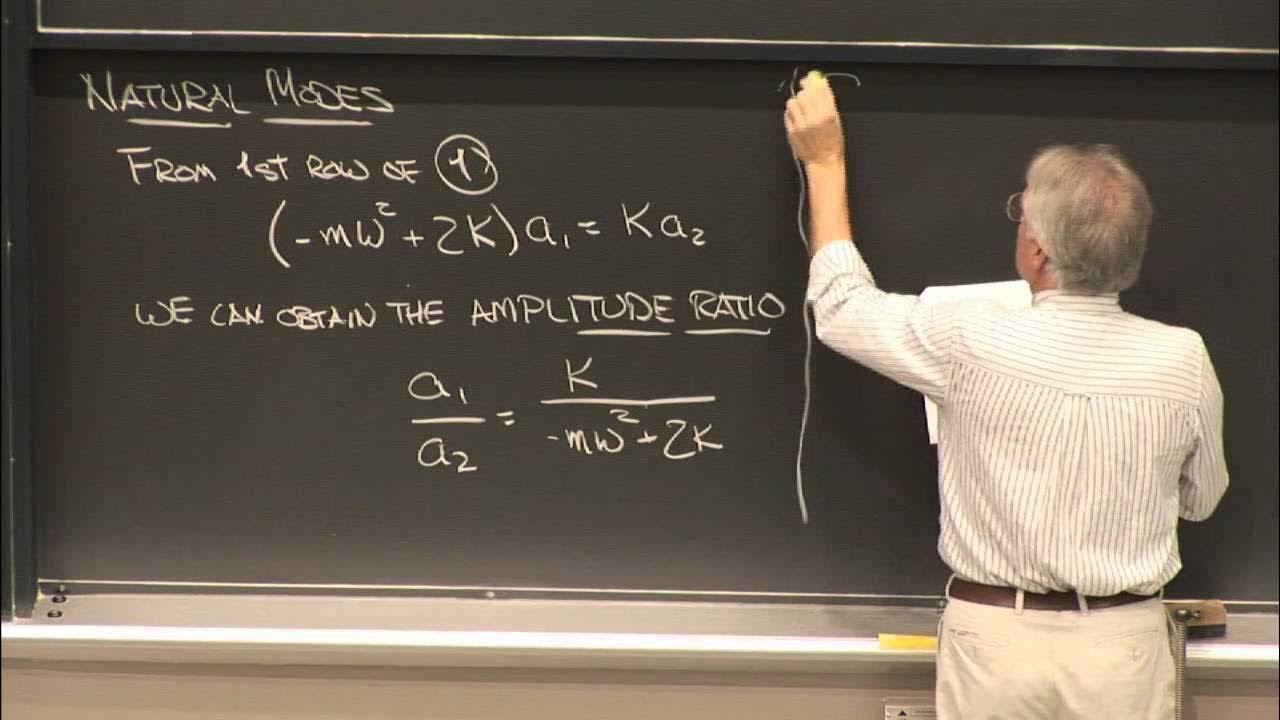7. Degrees of Freedom, Free Body Diagrams, & Fictitious Forces
TLDRThe MIT OpenCourseWare professor discusses the concept of 'muddy cards' for student feedback, emphasizing the importance of understanding coordinate systems, degrees of freedom, and free body diagrams in dynamics. He explains how angular momentum calculations vary with different reference points and clarifies misconceptions about vectors and coordinate independence. The lecture also covers the calculation of degrees of freedom, using various examples such as a wheel on a slope, a hockey puck on ice, and a rod leaning against a wall, to illustrate the constraints and independent coordinates needed to describe motion. The professor encourages the use of colored chalk and regular breaks for clarity and comprehension.
Takeaways
- 📚 The lecture emphasizes the importance of understanding coordinate systems, degrees of freedom, and free body diagrams in dynamics.
- 🔍 The concept of angular momentum computation from different points is highlighted, showing that it can yield different results, which is a crucial realization.
- 🤔 The discussion about vectors being independent of the coordinate system is addressed, explaining why angular momentum calculations can differ based on the point of reference.
- 👍 Positive feedback was given on the use of demos and examples in lectures, which aids in understanding complex concepts like angular momentum.
- 💬 A question from students about the dependency of vectors on coordinate systems was raised and clarified by the professor.
- 🌈 Suggestions from students, such as using colored chalk and taking breaks, were acknowledged and well-received by the professor.
- 🔄 The lecture revisits the topic of Coriolis and the selection of reference frames, indicating that these are common points of confusion that will be revisited.
- 📉 The use of 'muddy cards' for feedback was praised, and the professor commits to using them for ongoing lectures to enhance learning.
- 🧩 The calculation of degrees of freedom is explained with several examples, emphasizing the methodical approach needed to solve dynamics problems.
- 🧲 The role of constraints in problems involving rigid bodies is discussed, illustrating how they affect the degrees of freedom and the formulation of equations of motion.
- 🌀 The lecture introduces the concept of fictitious forces, particularly centrifugal force, in the context of rotating reference frames, and the importance of understanding the fundamentals when using them.
Q & A
What is the purpose of MIT OpenCourseWare and how can one support it?
-MIT OpenCourseWare aims to offer high-quality educational resources for free. Support can be provided through donations or by viewing additional materials from hundreds of MIT courses on their website at ocw.mit.edu.
What did the professor discuss regarding muddy cards in the lecture?
-The professor discussed the feedback received from the students' muddy cards, which contained comments about the lecture. The students appreciated the demos and explanations with examples, particularly the computation of angular momentum from two different points.
Why did the professor review the concept of angular momentum with respect to different points?
-The professor reviewed this concept because it was highlighted in the students' muddy cards as a point of confusion. The computation of angular momentum with respect to different points yields different answers, which led to a discussion about the independence of vectors from coordinate systems.
How does the definition of angular momentum with respect to a point change when the point is moved?
-According to the lecture, angular momentum with respect to a point is defined as the cross product of the position vector from the coordinate system's origin to the particle and the particle's linear momentum. When the point is moved, the position vector changes, leading to a different angular momentum vector.
What is the concept of degrees of freedom in dynamics?
-Degrees of freedom refer to the number of independent coordinates necessary to describe the motion of a system. It helps in determining the number of independent coordinates required to completely describe the motion without redundancy.
How can one calculate the number of degrees of freedom for a system involving rigid bodies and particles?
-The number of degrees of freedom can be calculated using the formula 6 times the number of rigid bodies plus 3 times the number of particles minus the number of constraints.
What is the significance of constraints in determining the degrees of freedom?
-Constraints are conditions that restrict the motion of a system. They are crucial in determining the degrees of freedom because each constraint reduces the number of independent coordinates needed to describe the system's motion.
Can you explain the difference between a rigid body and a particle in the context of dynamics?
-A particle is an idealization with mass but no size, while a rigid body is a larger entity with mass distributed throughout its extent. The rotational inertia of a rigid body matters, whereas for a particle, only its mass is considered in motion.
What is a free body diagram (FBD) and why is it important in solving dynamics problems?
-A free body diagram is a graphical representation that shows all the forces acting on a body in a system. It is important because it helps in visualizing and analyzing the forces and constraints that influence the motion of the body, which is essential for setting up equations of motion.
How does the assumption of no slip condition affect the degrees of freedom in a problem involving a wheel rolling down a slope?
-The no slip condition implies that the distance rolled down the slope is equal to the product of the radius of the wheel and the angle rolled. This makes the x-coordinate and the angular coordinate theta not independent of each other, effectively reducing the degrees of freedom by one.
What is the role of the center of mass in determining the motion of a system?
-The center of mass is the point where the mass of the system can be considered to be concentrated. It is important in determining the motion because Newton's second law applies to the motion of the center of mass, and it translates along with the system.
Outlines
📚 Introduction to MIT OpenCourseWare and Muddy Cards
The script begins with an introduction to MIT OpenCourseWare, emphasizing its mission to provide free, high-quality educational resources. It encourages donations to support this initiative and directs interested parties to the website for more materials. The professor then discusses 'muddy cards,' a feedback tool used to gather student impressions on lectures. The cards revealed that students appreciated practical demonstrations and clear explanations with examples, particularly regarding the computation of angular momentum from different reference points. The professor addresses a common misconception about the independence of vectors from coordinate systems, explaining the concept of angular momentum relative to different points and clarifying its dependency on the choice of reference point.
🔍 Exploring Degrees of Freedom and Constraints in Dynamics
This paragraph delves into the concept of degrees of freedom in dynamics, defined as the number of independent coordinates needed to describe motion. The professor outlines a formula to calculate degrees of freedom, which involves the number of rigid bodies, particles, and constraints present in a system. Using a wheel as an example, the professor illustrates how to identify constraints and calculate degrees of freedom, emphasizing the importance of understanding constraints like no motion in certain directions and no slip conditions to simplify the problem and derive the correct equations of motion.
🚀 Analyzing Rigid Body Dynamics with a Wheel on a Slope
The script continues with an analysis of a wheel on a slope, considering it as a rigid body and discussing the preliminary steps in setting up a coordinate system to study its motion. The focus then shifts to identifying constraints, such as the inability to move in certain directions and assumptions about the wheel's behavior, like no slipping. The professor calculates the number of degrees of freedom and explains how to use these insights to develop a free body diagram, which includes forces like gravity, normal force, and a tangential force that might prevent slipping.
🧩 Disassembling the Dynamics of a Hockey Puck with a String
The dynamics of a hockey puck wrapped with a string is the subject of this paragraph. The professor explains how to determine the number of degrees of freedom for the system, taking into account the constraints imposed by the surface and the string. The analysis involves considering the inability to move through the surface and the restrictions on rotation about certain axes. The professor then discusses the need for multiple equations of motion to fully describe the system's behavior, highlighting the importance of selecting appropriate coordinates and understanding the constraints.
🔄 Examining the Rotation and Translation of a Rod Against a Wall
The script presents a scenario involving a rod leaning against a wall, focusing on the concepts of translation and rotation. The professor discusses the constraints at the points of contact between the rod and the wall, explaining how these constraints affect the degrees of freedom. The analysis includes identifying the center of mass, the importance of the instantaneous center of rotation (ICR), and the implications for the motion of the rod. The professor emphasizes the need for a single coordinate to describe the rod's motion and the usefulness of the ICR in simplifying the equations of motion.
🤔 Reflecting on Unknowns in a Rod's Free Body Diagram
In this paragraph, the professor reflects on the unknowns present in the free body diagram of the rod from the previous example. The discussion revolves around identifying the forces acting on the rod, such as normal forces and gravity, and considering the implications of a frictionless environment. The professor highlights the need to find relationships between these unknowns to solve the equations of motion, mentioning the use of the instantaneous center of rotation and the relationship between torque and angular momentum.
🔄 Discussing the Degrees of Freedom for a System of Two Carts
The professor introduces a new example involving two carts connected by a spring and a dashpot, constrained by the floor. The focus is on calculating the degrees of freedom for this system, considering the constraints and the independent coordinates needed to describe the motion of both carts. The professor suggests that there are 10 constraints and that two independent coordinates are necessary, recommending the use of coordinates starting from the static equilibrium position for simplicity.
🤔 Assigning Free Body Diagrams for a System with Springs and Dashpots
This paragraph discusses the assignment of free body diagrams for the two-cart system with springs and dashpots. The professor explains the process of determining the direction of forces exerted by the springs and dashpots on each cart, emphasizing the importance of considering the system's positive motions to deduce these forces. The explanation includes the principles of superposition and the linear nature of the forces involved, leading to the formulation of equations of motion for the system.
🌀 Introducing Fictitious Forces and Their Application
The script shifts focus to the concept of fictitious forces, which are introduced as useful but potentially dangerous tools in physics. The professor explains that fictitious forces arise from considering the acceleration of a reference frame and can be treated as forces in the equations of motion. The paragraph includes a simple example of an elevator accelerating upwards, illustrating how to calculate the apparent weight of a person inside using the concept of fictitious forces.
🌀 Calculating Fictitious Forces in a Rotating Reference Frame
Building on the concept of fictitious forces, the professor presents a more complex example involving a mass attached to a rotating shaft. The analysis requires understanding the acceleration components in a rotating reference frame and identifying the forces that can be treated as fictitious. The professor breaks down the acceleration into its cylindrical coordinate components and discusses how to use these components to quickly estimate the torques and forces involved in the system.
🌀 Estimating Torques and Bending Moments Using Fictitious Forces
In this paragraph, the professor demonstrates how to use fictitious forces to quickly estimate torques and bending moments in a rotating system. The example involves a rotating shaft with a mass attached, and the professor shows how to calculate the torque caused by the centrifugal force and the bending moment it creates. The discussion highlights the importance of understanding the direction and magnitude of these fictitious forces and their implications for the design and analysis of rotating systems.
🚫 The Pitfalls of Fictitious Forces and the Importance of Real Forces
The script concludes with a cautionary note about the use of fictitious forces. The professor emphasizes the importance of distinguishing between real forces, such as gravity or contact forces, and fictitious forces, which are accelerations treated as forces for convenience. The professor advises that while fictitious forces can enhance intuition and provide quick estimates, one must always return to fundamental principles for rigorous analysis.
🔧 Preview of a Mechanical Shaker Demonstration
The final paragraph provides a brief preview of a mechanical shaker demonstration that will be discussed in the next session. The professor encourages students to fill out their muddy cards with questions or feedback, indicating a commitment to interactive and engaging teaching methods. The script ends with an anticipation of further exploration into the dynamics of mechanical systems.
Mindmap
Keywords
💡Muddy Cards
💡Angular Momentum
💡Coordinate System
💡Degrees of Freedom
💡Constraints
💡Free Body Diagram (FBD)
💡Rigid Body
💡Equations of Motion
💡Coriolis Force
💡Fictitious Forces
Highlights
The lecture discusses the importance of understanding coordinate systems and degrees of freedom in dynamics.
Positive feedback on the use of demos and examples in explaining complex concepts.
The concept of angular momentum computed from different points results in different answers, emphasizing the importance of the reference point.
The clarification that vectors are independent of the coordinate system, but their calculations can yield different results based on the reference point chosen.
The use of 'muddy cards' as a tool for students to provide feedback and ask questions, enhancing the interactive nature of the lecture.
The suggestion to use colored chalk for clearer explanations, which the professor agrees to implement.
The recommendation for the professor to take a break in the lecture for better student comprehension.
An in-depth discussion on how to calculate degrees of freedom for various mechanical systems, including a wheel on a slope and a rod against a wall.
The identification of constraints in a problem and how they affect the number of degrees of freedom.
The explanation of the difference between a rigid body and a particle in the context of rotational inertia.
The use of free body diagrams (FBDs) to visualize and calculate the forces and motion in a system.
The concept of Coriolis force is mentioned as a topic that students found challenging and will be revisited.
The importance of selecting appropriate reference frames for problem-solving in dynamics.
The strategy of simplifying problems by making reasonable assumptions to reduce the complexity of equations of motion.
The application of Newton's second law in the context of the motion of the center of mass in a system.
The discussion on the instantaneous center of rotation (ICR) and its role in calculating torques and moments in rotating systems.
The caution against the misuse of fictitious forces and the emphasis on understanding the fundamental principles behind them.
The illustration of how to calculate the bending moment on a shaft due to centripetal acceleration using the concept of centrifugal force.
The final example demonstrating the use of fictitious forces to quickly estimate torques in a rotating system, versus the rigorous approach using differential equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: