Slope Fields

RH Mathematics

16 Oct 202121:12

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video delves into the concept of slope fields, a graphical representation of differential equations, essential for solving them. The instructor explains how to sketch slope fields and solution curves, using 'dy/dx = 2x' and 'dy/dx = y' as examples. They highlight the importance of recognizing patterns and the general solution's form, such as 'y = x^2 + c' for the former. The video also guides viewers in identifying the differential equation from a given slope field and emphasizes the techniques for tackling multiple-choice questions in AP Calculus, focusing on eliminating incorrect answer choices based on the dependence of 'dy/dx' on 'x' and 'y'.

Takeaways

📚 The video introduces the concept of slope fields, which are graphical representations of differential equations.
🔍 A slope field is created by plotting the rate of change (dy/dx) against the independent variable (x) and dependent variable (y).
📈 The video demonstrates how to sketch a slope field for a given differential equation, emphasizing that the slope depends only on 'x' in the first example.
📝 The process of sketching involves drawing horizontal tick marks to represent the slope at different points on the graph.
🧩 The video identifies 'y = x^2' as a particular solution to the differential equation dy/dx = 2x, highlighting that any vertical shift of this parabola would still satisfy the equation.
🔑 The general solution to dy/dx = 2x is given as y = x^2 + c, where 'c' is any constant, illustrating the concept of a family of solutions.
🎯 The second example involves a differential equation where dy/dx depends only on 'y', leading to the identification of y = e^x as a solution.
🔍 The video shows how to analyze a slope field to determine whether the differential equation depends on 'x', 'y', or both.
📉 For AP Calculus, students are expected to sketch slope fields and solution curves, but not derive equations from slope fields without given information.
📝 When sketching solution curves, the emphasis is on following the general pattern of the slope field rather than trying to match each tick mark exactly.
📈 The video concludes with a multiple-choice task to determine the differential equation from a given slope field, using elimination based on the observed dependencies and slopes.

Q & A

What is the main topic of the video?
-The main topic of the video is slope fields and solving differential equations.
What is a differential equation?
-A differential equation relates a function, its independent variable (usually x), and its rate of change (dy/dx).
What is a slope field?
-A slope field is a graph that represents the differential equation, showing the slope of the function at various points.
Why does the instructor suggest focusing only on x when sketching a slope field?
-The instructor suggests focusing only on x because dy/dx depends only on x, not on y, simplifying the process.
What is the differential equation represented by the first slope field in the video?
-The differential equation for the first slope field is dy/dx = 2x.
What is a particular solution to the differential equation dy/dx = 2x?
-A particular solution to the differential equation dy/dx = 2x is y = x^2.
What is the general solution to the differential equation dy/dx = 2x?
-The general solution to the differential equation dy/dx = 2x is y = x^2 + c, where c is any constant.
What is the differential equation represented by the second slope field in the video?
-The differential equation for the second slope field is dy/dx = y.
What is the general solution to the differential equation dy/dx = y?
-The general solution to the differential equation dy/dx = y is y = ce^x, where c is any constant.
What are the three things that students need to be able to do with slope fields in AP Calculus?
-In AP Calculus, students need to be able to sketch slope fields, sketch solution curves, and understand how to fit solution curves to a given slope field.
How does the instructor suggest sketching solution curves in slope fields?
-The instructor suggests sketching solution curves by following the general pattern of the slope field, using a pencil, and not trying to jump from tick mark to tick mark.
What is the differential equation for the slope field where dy/dx is independent of x?
-The differential equation for the slope field where dy/dx is independent of x is dy/dx = y + 1.
What is the differential equation for the slope field where dy/dx depends only on x?
-The differential equation for the slope field where dy/dx depends only on x is dy/dx = 1/x.
How can you determine if a slope field depends on x or y?
-You can determine if a slope field depends on x or y by observing if the slope changes when you manipulate x or y. If the slope changes with x, it depends on x; if it changes with y, it depends on y.
What is a common mistake when sketching solution curves in slope fields?
-A common mistake is trying to jump from tick mark to tick mark, which results in a robotic and non-curve-like appearance. Instead, one should follow the general pattern of the slope field.
What is the differential equation for the slope field that has zero slopes when x equals negative one?
-The differential equation for the slope field that has zero slopes when x equals negative one is dy/dx = -y + y.

Outlines

00:00

📈 Introduction to Slope Fields

This video introduces slope fields as part of a unit on solving differential equations. It explains the concept of a differential equation, which relates a function, its independent variable, and its rate of change. The video begins by emphasizing that for the given differential equation, dy/dx depends only on x. The process of sketching slope fields by creating a three-column chart and plotting points is demonstrated. The importance of understanding the behavior of the function at different points is highlighted, with an example showing how to draw slope marks for x values and their corresponding dy/dx.

05:00

🧮 Sketching a Slope Field for dy/dx = y

This section continues with an exercise to sketch a slope field for the differential equation dy/dx = y. It explains that dy/dx depends only on y, and describes how to fill in the slope field accordingly. The pattern in this slope field is identified as exponential, specifically y = e^x, with y = 0 and y = -e^x as other potential solution curves. The general solution is given as y = Ce^x, where C is any constant, and further explanation is provided on how these solutions fit the slope field.

10:01

📝 Sketching Solution Curves and AP Calculus Requirements

This paragraph discusses the requirements for AP Calculus concerning slope fields, emphasizing the need to sketch slope fields and solution curves. It explains the method of sketching solution curves by following the general pattern of the slope field. The importance of extending the solution curve to the edges of the field and avoiding contradictions with the slope field is highlighted. Examples are provided to demonstrate how to sketch solution curves for different differential equations and how to identify patterns.

15:01

🔍 Identifying Differential Equations from Slope Fields

The focus here is on identifying differential equations from given slope fields. It outlines techniques to determine if dy/dx depends on x or y by observing the changes in slopes when moving left-right or up-down. Examples are provided to illustrate this method, showing how to derive potential differential equations based on the observed slope patterns. The importance of recognizing dependencies on x or y and how this can help eliminate incorrect answer choices in multiple-choice settings is discussed.

20:05

✅ Matching Slope Fields to Differential Equations

This final section covers a multiple-choice task of matching a given slope field to its corresponding differential equation. Strategies for elimination based on the dependence of dy/dx on x and y are emphasized. Specific examples are analyzed to demonstrate the process of identifying the correct differential equation. The goal is to understand how to use slope patterns to make educated guesses and eliminate incorrect options, with practical advice on how to approach such questions on assessments.

Mindmap

Keywords

💡Slope Fields

A slope field is a graphical representation of a differential equation. It consists of small line segments or arrows showing the direction of the slope at various points in the plane. In the video, slope fields are introduced as a tool to visualize differential equations, demonstrating how the slope at each point can help understand the behavior of solutions.

💡Differential Equation

A differential equation is a mathematical equation that relates a function with its derivatives. In the context of the video, it is explained as a relationship involving a function, its independent variable (usually x), and its rate of change (dydx). The video discusses how differential equations can be solved to recover the original function based on the information about its derivative.

💡dy/dx

dy/dx represents the derivative of y with respect to x, indicating the rate of change of y as x changes. The video emphasizes that dy/dx depends on x, which simplifies the process of plotting slope fields as it only requires consideration of x-values for determining slopes.

💡Solution Curve

A solution curve is a graph of a function that satisfies a given differential equation. In the video, it is shown how to sketch solution curves by following the slopes indicated in the slope field, demonstrating that a solution curve fits the behavior dictated by the differential equation.

💡Particular Solution

A particular solution is a specific solution to a differential equation that satisfies given initial conditions or specific values. For example, in the video, y = x^2 is identified as a particular solution to the differential equation dy/dx = 2x.

💡General Solution

A general solution to a differential equation includes all possible solutions, often expressed with an arbitrary constant. The video explains that for dy/dx = 2x, the general solution is y = x^2 + C, where C can be any constant, allowing for a family of parabolas.

💡Exponential Growth

Exponential growth refers to a situation where the rate of change of a quantity is proportional to the quantity itself, leading to rapid increases. In the video, the differential equation dy/dx = y is associated with exponential growth, and the function y = e^x is shown as a solution curve demonstrating this behavior.

💡Zero Slope

A zero slope indicates a horizontal line segment, representing no change in y as x changes. In the video, it is pointed out that at points where x is 0, the slope dy/dx = 0, resulting in horizontal tick marks in the slope field.

💡Asymptote

An asymptote is a line that a graph approaches but never touches or crosses. The video briefly touches on the concept while discussing the function y = ln(x), which has a vertical asymptote at x = 0, reflecting the behavior of the slope field for dy/dx = 1/x.

💡Independent Variable

The independent variable is the input or argument of the function, typically denoted as x. In the context of the video, it is mentioned that differential equations studied in the class usually involve x as the independent variable, determining the value of the derivative dy/dx.

Highlights

Introduction to slope fields and solving differential equations.

Differential equations relate a function, its independent variable, and its rate of change (dy/dx).

A slope field is a graph of a differential equation, showing the behavior of the function's slope at various points.

dy/dx depends only on x, so we can simplify calculations by ignoring y in certain cases.

Explanation of how to sketch slope fields using horizontal tick marks for slope at given points.

Demonstrating the slope field for dy/dx = 2x and how the slopes change at different x values.

Identifying patterns in slope fields to find a family of solution curves, like y = x^2.

General solutions to differential equations can include a constant (e.g., y = x^2 + C).

Task to sketch a slope field for dy/dx = y and identify its pattern.

Recognizing exponential patterns in slope fields, such as y = e^x for dy/dx = y.

Explanation of trivial solutions like y = 0 and their relevance to differential equations.

Overview of AP Calculus requirements for slope fields: sketching fields, sketching solution curves, and understanding general solutions.

Determining if dy/dx depends only on x or y by observing changes in slopes across columns or rows.

Example problem to match differential equations to slope fields by eliminating choices based on dependencies on x and y.

Final tips for sketching solution curves accurately and recognizing patterns in slope fields.

Transcripts

Browse More Related Video

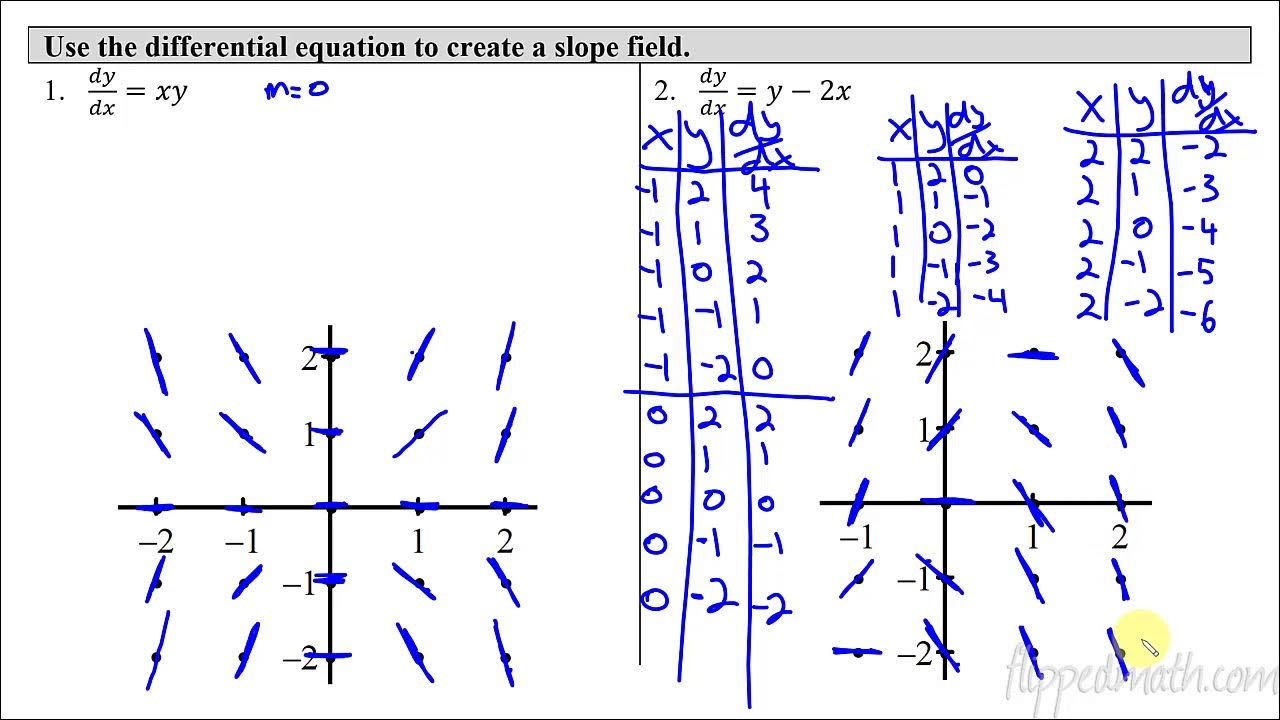
Calculus AB/BC – 7.3 Sketching Slope Fields

Differential equation from slope field | First order differential equations | Khan Academy

AP CALCULUS AB 2022 Exam Full Solution FRQ#5(a,b)

2005 AP Calculus AB Free Response #6

2015 AP Calculus AB Free Response #4

Creating a slope field | First order differential equations | Khan Academy

Related Tags

Differential Equations Slope Fields Educational Video Mathematics AP Calculus Solution Curves Derivatives Exponential Growth Logarithmic Functions Multiple Choice