Product Rule With 4 Functions - Derivatives | Calculus

The Organic Chemistry Tutor
17 Jan 202005:39
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the process of finding the derivative of a complex function involving four terms: x squared, sine x, e to the 4x, and the natural log of x. It introduces the product rule for derivatives, detailing how to apply it to multiple terms. The explanation includes calculating the derivatives of individual terms and combining them according to the rule. The final result is a simplified expression derived by factoring out the greatest common factor, e to the 4x, and presenting the terms with their respective derivatives. The video is an educational resource for those learning calculus and understanding the application of the product rule in more complex scenarios.

Takeaways
  • 📚 The problem involves finding the derivative of a complex function that is a product of four terms: x^2, sin(x), e^(4x), and ln(x).
  • 🧮 The product rule is essential for this problem, which states that the derivative of a product of two functions is the derivative of the first function times the second plus the first function times the derivative of the second.
  • 🔢 When dealing with more than two terms, extend the product rule by differentiating each term sequentially, keeping the others constant, and summing the results.
  • 🌟 The derivative of x^2 is found using the power rule, resulting in 2x.
  • 📈 The derivative of sin(x) is cos(x), a fundamental result from trigonometry.
  • 🌠 For the exponential function e^(4x), the derivative is calculated using the chain rule, resulting in e^(4x) * 4.
  • 📚 The natural log function's derivative, ln(u), with respect to x is (1/u) * u', where u is a function of x.
  • 🌿 The final expression can be simplified by factoring out the greatest common factor, which in this case is e^(4x).
  • 🔄 The process involves combining the derivatives of each term while maintaining the structure of the original function, leading to a simplified result.
  • 🎓 Understanding the product rule and how to apply it to multiple functions is crucial for solving complex derivative problems.
  • 👍 This video script serves as a comprehensive guide on using the product rule for functions with multiple terms, providing a step-by-step breakdown of the process.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is finding the derivative of a complex function that involves a product of four terms using the product rule.

  • What is the product rule mentioned in the script?

    -The product rule mentioned in the script is a calculus formula used to find the derivative of a product of two or more functions. It states that the derivative of a product of functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function.

  • How does the script generalize the product rule for more than two terms?

    -The script generalizes the product rule for more than two terms by expanding it to a sum of products, where each term is the derivative of one function times the remaining functions, keeping them constant during the differentiation process.

  • What is the derivative of x squared?

    -The derivative of x squared, using the power rule, is 2x (x raised to the power n becomes n times x to the power n-1).

  • What is the derivative of sine x?

    -The derivative of sine x is cosine x.

  • How does the script find the derivative of e to the 4x?

    -The script uses the chain rule for exponential functions, which states that the derivative of e to the u with respect to x is e to the u times the derivative of u. Here, u is 4x, so the derivative is e to the 4x times 4.

  • What is the derivative of the natural log of x?

    -The derivative of the natural log of x (ln x) is 1 divided by x, since the derivative of ln u (where u is a function of x) is 1/u.

  • How does the script simplify the final expression?

    -The script simplifies the final expression by factoring out the greatest common factor, e to the 4x, from all terms. This leaves terms involving x squared, sine x, cosine x, ln x, and their respective derivatives.

  • What is the significance of the GCF in the simplification process?

    -The significance of the GCF (Greatest Common Factor) in the simplification process is that it helps to reduce the complexity of the expression, making it easier to understand and work with.

  • How does the script conclude?

    -The script concludes by summarizing the process of using the product rule for a product of four functions and emphasizes that this is a method that can be applied to similar problems.

  • What is the final simplified derivative found in the script?

    -The final simplified derivative found in the script is e to the 4x times the sum of 2x sine x ln x, x squared cosine x ln x, 4x squared sine x ln x, and x sine x.

Outlines
00:00
📚 Derivative of a Complex Product Function

This paragraph introduces the challenge of finding the derivative of a complex function that is a product of four terms. It explains the use of the product rule for derivatives, which is essential for solving such problems. The explanation begins with breaking down the problem into simpler parts, using the power rule to find the derivative of x squared, and then proceeding to find the derivatives of sine x, e to the 4x, and the natural log of x. The paragraph emphasizes the step-by-step process of applying the product rule, factoring in each term's derivative while keeping the others constant. It also touches on simplifying the expression by factoring out the greatest common factor, e to the 4x, to make the final expression more manageable.

05:01
🎓 Simplifying the Derivative Expression

In this paragraph, the focus is on simplifying the derived expression from the previous discussion. It details the process of combining the derivatives of each term while adhering to the product rule. The paragraph explains how to simplify the expression by grouping terms with common factors, such as e to the 4x, and then combining them to form the final simplified derivative. The paragraph concludes by summarizing the entire process of using the product rule for a product of four functions and highlights the importance of this technique in calculus. It ends with a note of thanks to the viewers for their attention and participation.

Mindmap
Keywords
💡Derivative
The derivative is a fundamental concept in calculus that represents the rate of change or the slope of a function at a particular point. In the context of the video, it is used to find the derivative of a complex function that involves multiple terms, specifically x^2, sin(x), e^(4x), and ln(x). The process of finding the derivative involves applying the product rule and understanding how it changes as you vary the input (x).
💡Product Rule
The product rule is a mathematical principle used in calculus to find the derivative of a product of multiple functions. It states that the derivative of a product of functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function. In the video, the product rule is applied to a product of four functions, and it is used to break down the complex expression into simpler parts to find the overall derivative.
💡Power Rule
The power rule is a basic calculus formula used to find the derivative of a function where the variable is raised to a constant power. It states that the derivative of x^n, where n is a constant, is n*x^(n-1). In the video, the power rule is applied to the term x^2, resulting in 2x, which is a key step in finding the derivative of the entire expression.
💡Sine Function
The sine function is a trigonometric function that relates the angle of a right triangle to the ratio of the length of the opposite side to the length of the hypotenuse. In the context of the video, the derivative of the sine function is needed when applying the product rule. The derivative of sin(x) is cos(x), which is used in the calculation of the complex derivative.
💡Exponential Function
An exponential function is a mathematical function where the base is a constant and the exponent is the variable. The function has the form e^u, where e is the base of the natural logarithm and u is the variable. In the video, the exponential function e^(4x) is part of the complex expression, and its derivative is found using the chain rule, resulting in e^(4x) * 4, which is then multiplied by the other terms as per the product rule.
💡Natural Logarithm
The natural logarithm, often denoted as ln or log_e, is the logarithm to the base e (where e is the mathematical constant approximately equal to 2.71828). It is the inverse function of the exponential function and is used extensively in calculus and mathematical analysis. In the video, the derivative of the natural logarithm function ln(x) is needed, which is found to be 1/x.
💡Chain Rule
The chain rule is a fundamental principle in calculus used to find the derivative of a composite function, which is a function made up of one function nested inside another. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function. In the video, the chain rule is implicitly used when calculating the derivative of the exponential function e^(4x), where the inner function is 4x and the outer function is e^u.
💡Greatest Common Factor (GCF)
The greatest common factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. In the context of the video, the GCF is used to simplify the expression by factoring out common terms, which in this case is e^(4x) that appears in all four parts of the derivative expression.
💡Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles and sides of a right triangle. The most common trigonometric functions include sine, cosine, and tangent. In the video, specifically the sine function is used as part of the complex expression, and its derivative is calculated using the product rule.
💡Alphabetical Order
Alphabetical order refers to the arrangement of items in a sequence according to the alphabetical system, from A to Z. In the video, the term 'alphabetical order' is used to describe the systematic approach to applying the product rule to a product of multiple functions, ensuring that each function's derivative is calculated and included in the correct sequence.
💡Simplifying Expressions
Simplifying expressions in mathematics involves reducing complex expressions to their simplest form by combining like terms, factoring, or using other algebraic techniques. In the video, the process of simplifying is crucial for making the derivative expression more understandable and manageable. This is achieved by factoring out common terms like e^(4x) and combining similar terms.
Highlights

Introduction to the problem of finding the derivative of a product of four terms.

Explanation of the product rule for derivatives with two terms.

Expansion of the product rule to three terms.

Generalization of the product rule for four terms.

Derivation process begins with the derivative of (x^2).

Keeping the first term constant and finding the derivative of sine (x).

Keeping the first two terms constant and finding the derivative of (e^(4x)).

Final step: finding the derivative of the natural log of (x).

Simplification process by factoring out the greatest common factor.

The result after factoring out (e^(4x)) from all four terms.

First term simplified: (2x * sin(x) * ln(x)).

Second term simplified: (x^2 * cos(x) * ln(x)).

Third term simplified to include the derivative of (e^(4x)).

Final simplification of the fourth term.

Conclusion of the derivative simplification process.

Summary of how to use the product rule with four functions.

Transcripts

Browse More Related Video

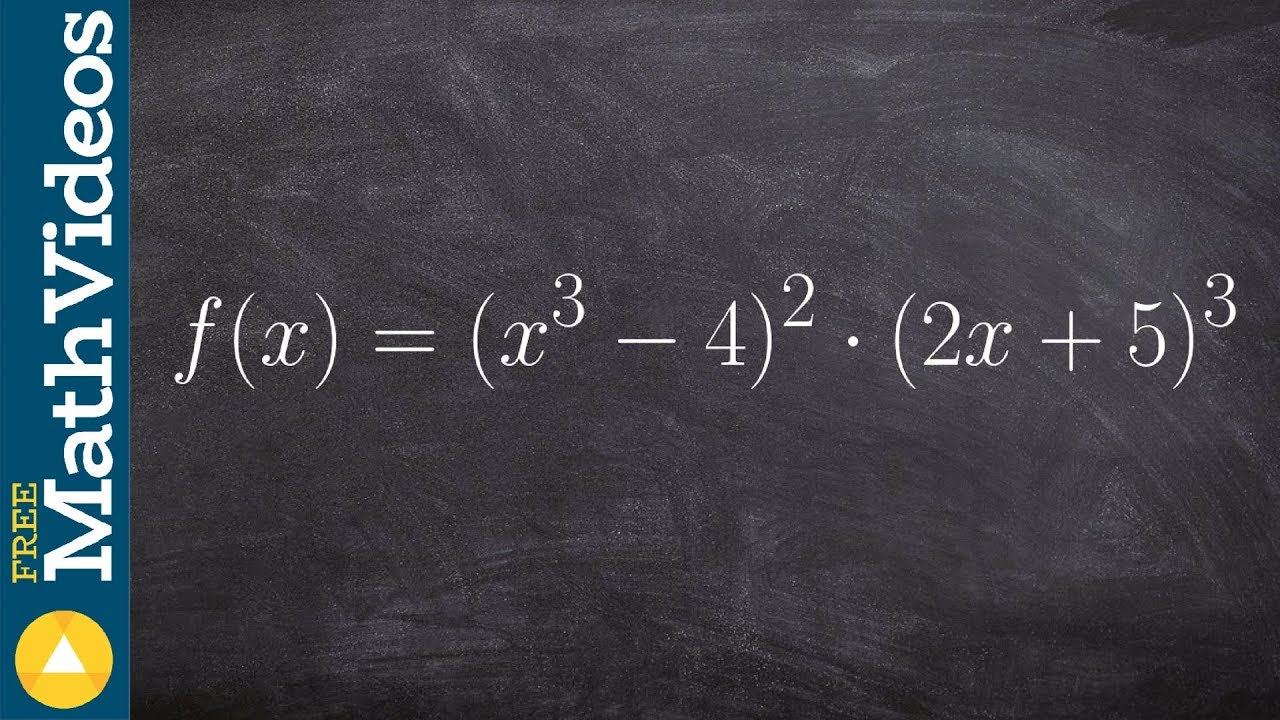
How to take the derivative with chain rule inside product rule

Derivative of e_____cos(e_) | Advanced derivatives | AP Calculus AB | Khan Academy

Logarithmic functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy

Product Rule With 3 Functions - Derivatives | Calculus

Implicit Differentiation for Calculus - More Examples #2

Calculus - Integration By Parts

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativesProduct RuleCalculusMathematicsTutorialEducationComplex Functionse^xTrigonometryLogarithms