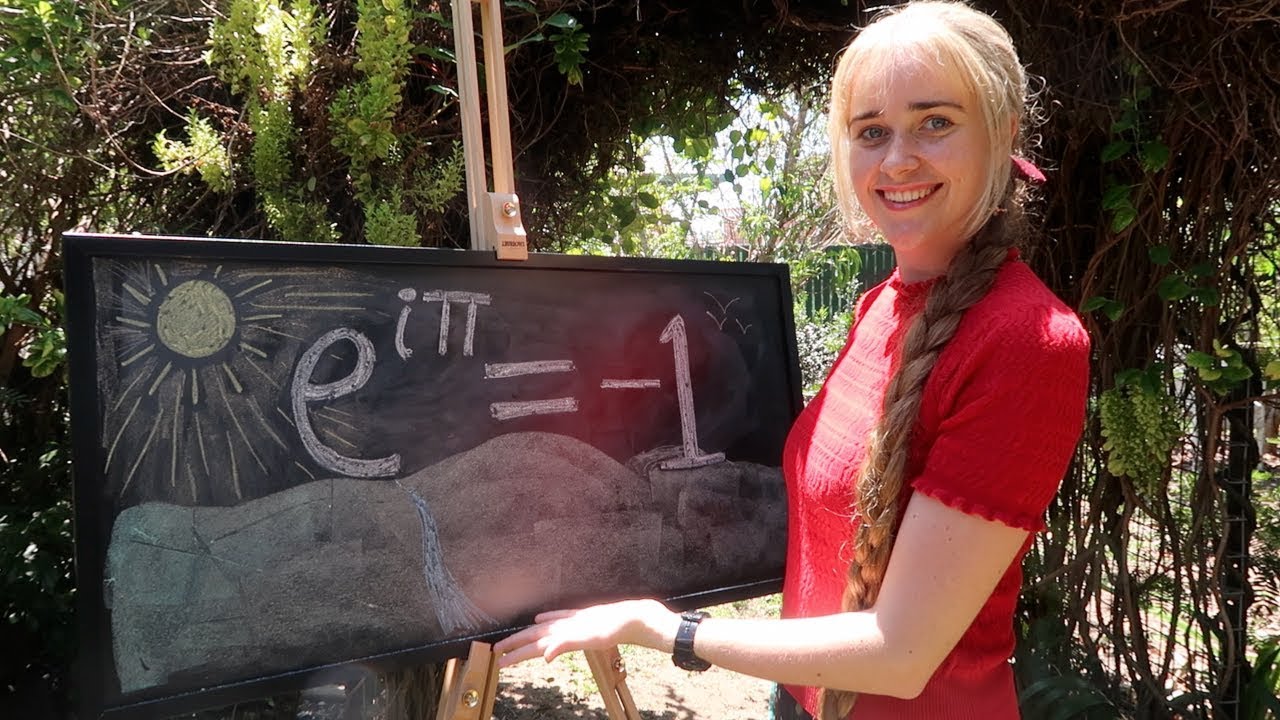Parabolas explained Bob Ross style
TLDRIn this episode of 'The Joy of Mathematics,' Toby invites viewers to indulge in mathematical artwork without the stress of equations. The video begins with a simple yet aesthetically pleasing scene painting, dividing the canvas into a blue sky and green grassy field. Toby then introduces a whimsical mushroom and strategically places a hill, using visual estimation rather than a ruler to find the perfect balance in the artwork. The creative process continues with the inclusion of 'happy little trees' and pine cones, which lead to an exploration of the shapes found within a cone, revealing the parabola. Toby demonstrates that parabolas are not only present in art but also abundant in nature and human-made structures, such as satellite dishes and fountains. He explains the practical applications of parabolas in reflecting light and their significance in various fields. The episode concludes with a call to observe mathematical shapes in everyday life and an invitation to share artwork that incorporates parabolas. Toby also thanks the sponsor, brilliant.org, for promoting mathematical curiosity and problem-solving skills.
Takeaways
- 🎨 The video is about creating mathematical artwork without the stress of equations, aiming to appreciate the mathematical world in a relaxed manner.
- 🌞 The artwork begins with a blue sky and adds elements like sunlight and birds, reflecting the beauty of nature through mathematical concepts.
- 🌿 The grass is depicted with a touch of reality, showing that it's not always green and can be influenced by environmental factors like smoke haze from bush fires.
- 🍄 A mushroom is placed in the artwork to add a magical element, showing that mathematics can be whimsical and fun.
- 🏞️ A hill is drawn using aesthetic judgment rather than a ruler, emphasizing the idea that not everything needs to be perfect to convey a mathematical concept.
- 📏 The shape of the hill is discovered to be a parabola, a shape that appears naturally and can be found in various forms in the environment.
- 📐 The concept of a parabola is introduced through the cutting of a pine cone, demonstrating that mathematical shapes are all around us.
- 🌳 Trees are added to the hill, with a focus on happy little pine cones, which are favorite shapes of the artist due to their interesting geometric properties.
- 🚀 Parabolas are shown to occur naturally in the trajectory of thrown objects and in the design of man-made structures like satellite dishes and fountains.
- 💡 Parabolas have practical applications, such as focusing light in solar heating and car headlights, highlighting the utility of mathematical shapes in technology.
- 🎨 The video encourages viewers to look for mathematical shapes in their surroundings and to create their own artwork incorporating parabolas.
- 🎁 The sponsor, brilliant.org, is highlighted for nurturing curiosity and problem-solving skills through its educational content on mathematics.
Q & A
What is the theme of today's episode of The Joy of Mathematics?
-The theme of today's episode is creating mathematical artwork, focusing on appreciating the mathematical world through art without the stress of equations.
How does Toby plan to start the artwork?
-Toby plans to start the artwork by splitting it in two, creating a line that separates the sky from the grass.
What colors does Toby use to represent the sky and the grass in the artwork?
-Toby uses blue to represent the sky and green to represent the grass.
Why is the grass in the backdrop behind Toby not as green as usual?
-The grass is not as green due to it being a little dry and smoky from the haze caused by bush fires.
What magical element does Toby decide to include in the artwork?
-Toby decides to include a mushroom that would attract fairies to add a bit of magic to the artwork.
How does Toby determine the placement of the hill in the artwork?
-Toby determines the placement of the hill by measuring it to be equidistant from the horizon and the mushroom, placing it right in the middle of these two.
What shape does Toby discover within a pine cone?
-Toby discovers that a pine cone contains shapes like a circle and an ellipse when cut in different ways.
What is the name of the shape that Toby finds in multiple places, including the hill and the cut-out from the cone?
-The shape is called a parabola.
How do parabolic shapes appear in nature and man-made objects?
-Parabolas occur naturally in the curve of dishes, the falling water of a fountain, and the path of an object thrown into the air. They are also used in man-made objects like solar dishes and car headlights for their reflective properties.
What property of parabolas makes them useful in applications like solar dishes and car headlights?
-Parabolas have the property of reflecting all parallel light rays to a focus, which is useful for concentrating light or energy.
How does Toby encourage viewers to engage with the mathematical shapes found in the episode?
-Toby encourages viewers to look out for mathematical shapes in their surroundings and to create their own artwork incorporating parabolas, offering to share the best ones on Twitter.
What is the purpose of the Brilliant premium subscription mentioned in the episode?
-The Brilliant premium subscription is a way to nurture curiosity, build confidence, and develop problem-solving skills by providing content that breaks down complex mathematical concepts into understandable chunks.
Outlines
🎨 Mathematical Artwork Creation
In this segment, Toby, the host of The Joy of Mathematics, warmly welcomes viewers back for another episode. He sets a relaxed and creative tone for the day's activity, which involves creating mathematical artwork without the use of equations. Toby outlines the day's plan to appreciate the mathematical world through art. He begins by dividing the artwork into two parts: the sky and the grass, using blue for the sky and green for the grass. He adds sunlight and birds to the sky and mentions the real-world context of the day's backdrop, which is affected by bush fires. Toby then introduces a whimsical element to the artwork by placing a fairy-attracting mushroom in the grass and planning to draw a hill for it to sit on. He emphasizes the aesthetic balance of the hill's position, neither too close to the horizon nor the mushroom, and uses mental estimation rather than a ruler to achieve this. The segment concludes with Toby adding happy little trees to the hill, celebrating the festive season with a pine cone, and humorously considering wearing the cone as a hat.
📐 Exploring Parabolas in Nature and Art
This paragraph delves into the fascinating geometry of cones and their inherent shapes. Toby uses a physical cone to demonstrate that by making different cuts, one can obtain a circle or an ellipse. He then proceeds to cut the cone in a way that parallels one of its sides, resulting in a shape that matches the hill drawn in the artwork. This shape is identified as a parabola. Toby explains that parabolas are ubiquitous in nature and human-made structures, providing examples such as the curves of satellite dishes and the trajectory of water in a fountain. He also discusses the practical applications of parabolas, such as reflecting light rays to a focus, which is utilized in solar heating and lighting fixtures. The segment ends with Toby encouraging viewers to incorporate parabolas into their own artwork and to share their creations. He also thanks the sponsor, brilliant.org, for their support and promotes their premium subscription as a gift to foster a love for math and learning.
Mindmap
Keywords
💡Mathematical Artwork
💡Parabola
💡Focus
💡Equidistant
💡Sponsor
💡Brilliant.org
💡Patrons
💡Cone and Ellipse
💡Hill
💡Smoke Haze
💡Pine Cones
Highlights
Toby introduces a new episode of The Joy of Mathematics focusing on mathematical artwork without equations.
The concept of creating a mathematical scene by dividing the artwork into a sky and grass landscape.
Adding elements of sunlight and birds to the sky to enhance the artwork.
Incorporating the current environmental context, such as dry grass and smoke haze from bush fires, into the artwork.
Introducing a magical element by placing a fairy-attracting mushroom in the grass.
Aesthetically placing a hill in the artwork at an equidistant point between the horizon and the mushroom.
Choosing to measure and draw the hill using visual estimation rather than a ruler for a more organic look.
Adding happy little trees and pine cones to the hill, celebrating the festive season with a real pine cone.
Exploring the shapes within a pine cone and demonstrating how it can be cut to form a circle or an ellipse.
Discovering the parabola shape within the cut of a cone and relating it to the drawn hill in the artwork.
Highlighting the natural and man-made occurrences of parabolas, such as in dishes and fountains.
Describing the physical properties of parabolas, specifically their ability to reflect parallel light rays to a focus.
Giving examples of how humans have utilized parabolas in technology, such as in solar heating and car headlights.
Encouraging viewers to add more color and parabola-shaped hills to their artwork for aesthetic appeal.
Inviting viewers to incorporate parabolas into their own artwork and share it for a chance to be featured on Twitter.
Promoting the sponsor brilliant.org and its premium subscription as a gift to nurture curiosity and problem-solving skills.
Expressing gratitude to patrons and showcasing the 'cat of the day' submitted by Rob.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: