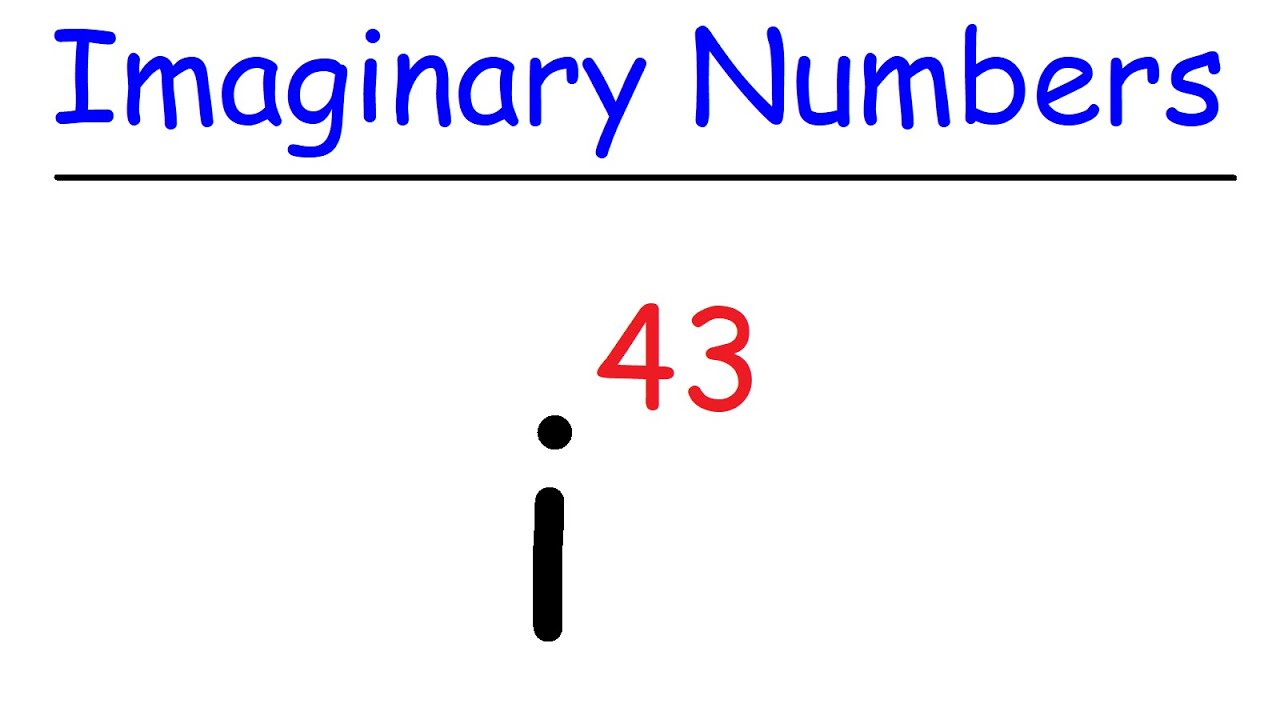
Imaginary Numbers Explained Bob Ross Style
TLDRIn this video, Toby invites viewers to embark on a mathematical journey that transcends reality. He shares personal stories about his early encounters with negative and imaginary numbers, which sparked his curiosity and fascination with these abstract concepts. The video explains the basics of imaginary numbers, their role in extending the scope of mathematics, and their practical applications, such as modeling circular or rotating phenomena. Toby uses the concept of 'imaginary friends' to illustrate the multiplication and rotation properties of imaginary numbers, demonstrating how multiplying by i (the imaginary unit) results in a 90-degree rotation, and how this can be used for navigation or in physics to describe electromagnetic waves. The video also highlights the importance of the complex plane, where numbers have both real and imaginary parts, and introduces the concept of complex multiplication. Toby encourages viewers to explore complex numbers further through a sponsored course on Brilliant, emphasizing the value of hands-on problem-solving to solidify mathematical understanding.
Takeaways
- 🌟 Mathematics can be a relaxing and joyful journey, offering a way to escape from reality through the exploration of abstract concepts.
- 🔢 Negative numbers and imaginary numbers both extend the realm of mathematics by introducing intangible yet useful ideas, such as numbers less than zero and the square root of negative one.
- 🌐 The concept of imaginary numbers was initially introduced as a way to understand the square root of negative one, which is represented by the imaginary unit 'i'.
- 🤔 Imaginary numbers, despite their name, are real and have practical applications in modeling circular or rotating phenomena.
- 📈 Multiplying by 'i' results in a 90-degree rotation, which is a key property used in the complex plane for modeling rotations.
- 🔄 The multiplication of imaginary numbers allows for movement around a circle, which is why they are effective in modeling circular or rotating systems.
- 🧭 Complex numbers, which combine real and imaginary parts, can be used for navigation and performing rotations in a plane, as illustrated by the forest walk example.
- 🔗 The imaginary unit 'i' is closely related to the concept of complex numbers, which have real-world applications such as in the wave function of electromagnetic waves.
- 📚 Learning platforms like Brilliant offer courses that delve deeper into complex numbers, including topics like complex multiplication, polar coordinates, and Euler's formula.
- 📈 To solidify knowledge in mathematics, it's important to engage in problem-solving and practical application, which is facilitated by interactive learning environments.
- 🌐 The complex plane, with its real and imaginary axes, allows for the exploration of a second dimension in numbers, adding depth to mathematical understanding.
- 🎓 The video encourages viewers to continue their mathematical journey, emphasizing the importance of community and support from platforms like Brilliant and Patreon.
Q & A
What was the speaker's first encounter with the concept of negative numbers?
-The speaker's first encounter with negative numbers was when a classmate claimed to know about secret numbers less than zero, which were called negative numbers. The speaker was initially doubtful and felt left out.
How did the speaker describe the introduction to imaginary numbers in high school?
-The introduction to imaginary numbers occurred when a substitute teacher, possibly the careers counselor, deviated from the lesson plan and introduced the concept of imaginary numbers by drawing axes labeled 'real' and 'imaginary'.
What is the mathematical significance of multiplying by 'i'?
-Multiplying by 'i' (the imaginary unit) results in a 90-degree rotation in the complex plane, making imaginary numbers useful for modeling circular or rotating phenomena.
How does the speaker use imaginary numbers to illustrate the concept of traveling between the real and imaginary worlds?
-The speaker uses the concept of imaginary friends, where each friend represents a multiplication by 'i', to explain how one can metaphorically travel between the real and imaginary worlds through mathematical operations.
What is the real-world application of complex numbers as mentioned in the script?
-Complex numbers are used to model phenomena that are circular in nature or involve rotation. An example given is the wave function of electromagnetic waves, where the electric and magnetic fields can be represented as real and imaginary parts of a complex number, respectively.
How does the script explain the concept of the complex plane?
-The complex plane is explained as a two-dimensional space where each point can be represented by an ordered pair consisting of a real part and an imaginary part, allowing for the representation of numbers that are not just real or imaginary but a combination of both.
What is the significance of 'i' to the power of zero in mathematics?
-In mathematics, any non-zero number raised to the power of zero is equal to one. This is a quirky mathematical fact that the script uses to illustrate the concept that starting with no imaginary friends (i^0) keeps one in the real world.
How does the multiplication of complex numbers relate to changing directions, as depicted in the forest walk example?
-The multiplication of complex numbers can be used to perform rotations in the complex plane. In the forest walk example, multiplying the initial direction (represented as a complex number) by another complex number representing a 45-degree rotation allows one to change their path accordingly.
What is the role of the imaginary unit 'i' in the context of the video?
-The imaginary unit 'i' is used as a metaphorical 'friend' that helps the speaker transition between the real and imaginary worlds. It also represents the mathematical concept of the square root of negative one.
How does the script use the concept of imaginary numbers to enhance the understanding of mathematics?
-The script uses the concept of imaginary numbers to show how mathematics can expand beyond the tangible and familiar, introducing a new dimension for exploration. It also demonstrates the practical applications of these abstract concepts in modeling real-world phenomena.
What is the final message the speaker conveys about imaginary numbers?
-The final message is that despite their name, imaginary numbers are not just imaginary; they have real-world applications and are a fundamental part of mathematics, providing an additional dimension for understanding and solving complex problems.
Outlines
😀 Introduction to the Imaginary World of Mathematics
The first paragraph introduces Toby, the host, who welcomes the audience back to the joy of mathematics. He sets the stage for an escape from reality through mathematics, mentioning how others might escape through various activities, but he offers a unique tour of an imaginary world with the help of 'imaginary friends.' Toby shares a personal story from his childhood about learning about negative numbers and his experience in high school learning about imaginary numbers. He explains the concept of imaginary numbers, i, and how it extends the realm of mathematics by asking what the square root of -1 might be. He also touches on the importance of acknowledging the real world and its consequences, before delving into the mathematical concept of imaginary numbers with a playful approach, introducing imaginary friends named Ignatio and Iguana to illustrate the transition between the real and imaginary worlds.
🌀 Exploring the Complex Plane and Rotations
The second paragraph delves deeper into the concept of imaginary numbers, explaining how multiplying by the imaginary unit i results in a 90-degree rotation, which is visualized on a map that includes points 1, i, -1, and -i. Toby uses the analogy of traveling between these points to describe the mathematical journey between the real and imaginary realms. He further explains that multiplying by -1 results in a 180-degree rotation, flipping between 1 and -1. The paragraph also highlights the utility of imaginary numbers in modeling circular or rotating phenomena. Toby emphasizes that imaginary numbers are real and have practical applications, despite being less tangible. He also discusses the concept of the complex plane, where a real part and an imaginary part are necessary to define a location, and provides a practical example of how to use complex number multiplication for rotation, such as changing one's direction while navigating a forest path.
📚 Embracing the Power of Imaginary Numbers in Mathematics
The third paragraph serves as a conclusion and a call to action. Toby encourages viewers to solidify their knowledge by trying problems for themselves, emphasizing the importance of active learning. He then introduces Brilliant, a platform for learning complex topics in a fun and challenging way, and mentions a course on complex numbers featuring characters Julia and Mandelbrot. Toby also provides a link for viewers to join the learning community. He concludes by thanking his Patreon supporters, giving a special shoutout to the Patreon cat of the day, Mina, and wishes everyone a mathematical day ahead.
Mindmap
Keywords
💡Negative Numbers
💡Imaginary Numbers
💡Complex Plane
💡Rotation
💡Complex Numbers
💡Multiplication
💡Real World
💡Imaginary Friends
💡Euler's Formula
💡Brilliant.org
💡Wave Function
Highlights
The video is a relaxing journey through mathematics, exploring the concept of imaginary numbers.
Toby shares a personal story about his first encounter with negative numbers as a child.
High school experience with a relief teacher introduces the concept of imaginary numbers.
Negative numbers and imaginary numbers are similar in that they both extend the realm of mathematics.
Imaginary numbers are useful, tangible ideas, despite their intangible nature.
The imaginary unit 'i' is derived from the question of what the square root of minus one might be.
Multiplication by 'i' is a 90-degree rotation, which is useful for modeling circular or rotating phenomena.
The complex plane allows for travel anywhere with a real and imaginary part.
Complex numbers can be used for performing rotations, such as changing direction while navigating.
An example of using complex numbers to navigate a 45-degree change in direction in the forest.
Imaginary numbers are not just theoretical; they have practical applications in fields like electromagnetism.
The video mentions Brilliant.org as a resource for learning complex numbers and related topics.
Brilliant's courses on complex numbers include complex multiplication, polar coordinates, and Euler's formula.
The importance of practicing problems to solidify knowledge in mathematics is emphasized.
The video concludes with a call to join a community of learners and educators on Brilliant.org/tibees.
A special mention is given to Patreon supporters and the 'Patreon cat of the day' Mina.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: