Square roots explained Bob Ross style

Tibees
4 Oct 201910:54
EducationalLearning
32 Likes 10 Comments

TLDRIn the 'Joy of Mathematics' video, Toby takes viewers on an analogy-rich journey to understand the concept of square roots. Using the metaphor of a tree and its roots, he explains that just as a tree's roots are crucial for its survival, understanding the underlying principles of mathematics is key to grasping complex ideas. Toby covers how to calculate square roots, introduces the radical symbol, and discusses its possible origins. He also touches on the concept of perfect squares, non-perfect squares, and the inclusion of imaginary numbers in square roots. The video concludes with an encouragement to explore the unseen 'roots' of knowledge and a wish for a mathematically inspired day.

Takeaways
  • 🌳 The visible part of a tree is like an iceberg, with the majority of its structure (roots) hidden underground, just as logarithms help us understand the underlying structure of exponents.
  • 📐 Square numbers, such as 9, 16, and 25, are the product of a whole number multiplied by itself, and they represent the area of a square with equal sides.
  • 🔍 To find an unknown base of a square, we use the square root, which is analogous to the roots of a tree providing support and nourishment.
  • 🍎 The concept of square roots can be visualized by dividing the area of a square into a grid, where the number of units corresponds to the square root's value.
  • 🔢 Perfect squares are the results of squaring whole numbers, and non-perfect squares like 20 have square roots that are not whole numbers but can be approximated.
  • ➕ There are two solutions to every square root equation, the positive and the negative, but in many practical applications, only the positive solution is considered.
  • 🤔 The square root symbol, resembling a heartbeat, has various origin stories, including possible links to the Arabic and Latin words for 'root', and an evolution from dots above numbers.
  • 📜 Descartes was the first to use the modern square root symbol with a vinculum, indicating the inclusion of all numbers under the root.
  • 📊 The principal square root typically refers to the non-negative root, but equations involving squared variables can have both positive and negative solutions, expressed as ±.
  • 🈵 Squaring any real number, whether positive or negative, results in a non-negative number, meaning real numbers do not have real square roots if they are negative.
  • 🧮 By introducing imaginary numbers, we can extend the concept of square roots to include negative numbers, with i being the square root of -1.
  • 🌟 The story of square roots is a reminder of the hidden depths and structures in mathematics, encouraging exploration and understanding of the unseen.
Q & A

  • What is the main analogy used in the script to describe the importance of roots to a tree?

    -The main analogy used is that a tree is like an iceberg, where the visible part above the ground is only a small part of the story, and the roots underground are crucial for the tree's existence, much like how logarithms and square roots are fundamental to understanding certain mathematical concepts.

  • What does the script suggest about the relationship between the square root and the area of a square?

    -The script suggests that the square root of a number is directly related to the area of a square whose sides are equal to that number. For example, the square root of 16 is 4 because a square with sides of length 4 units has an area of 16 square units.

  • What are perfect squares and why are they called so?

    -Perfect squares are the results of squaring whole numbers. They are called 'perfect' because they are the exact squares of integers, such as 9 (3 squared), 16 (4 squared), and 25 (5 squared).

  • How does the script explain the concept of a non-perfect square and its square root?

    -The script explains that a non-perfect square, like 20, is a number that is not the exact square of an integer. Its square root is a decimal because it lies between the square roots of the nearest perfect squares (4 and 5), and is approximately 4.47.

  • What is the significance of the symbol used for square roots, and what are some of its possible origins?

    -The symbol for square roots, often referred to as the radical symbol, is significant as it denotes the operation of finding a number's square root. Possible origins include the Arabic word for root, the Latin word 'radix', or an evolution from dots used to denote square roots above numbers.

  • Who was the first to use the square root symbol with a line over the top, and what is this line called?

    -René Descartes was the first to use the square root symbol with a line over the top in 1637. This line is called the vinculum, and it signifies that all the numbers under it are included in the square root operation.

  • What does the script imply about the existence of square roots for negative numbers in the real number system?

    -The script implies that in the real number system, negative numbers do not have real square roots because squaring any real number, whether positive or negative, results in a positive value.

  • How does the script introduce the concept of imaginary numbers?

    -The script introduces imaginary numbers by suggesting that if we define 'i' as the square root of -1, we can then calculate the square root of negative numbers, such as -16, which would result in 4i.

  • What is the moral of the story presented in the script?

    -The moral of the story is that one should not be limited by traditional thinking and should be open to exploring beyond conventional boundaries, as exemplified by the ability to find square roots for not just real numbers, but also for imaginary numbers.

  • How does the script use the tree analogy to relate to the concept of support in life?

    -The script uses the tree analogy to relate the concept of support in life by stating that just as a tree's roots provide it with nutrients and support, allowing it to grow, support in life can make achieving great things feel easier, even though it may be hard to come by or recognize.

  • What is the significance of the 'heartbeat' symbol used for square roots?

    -The 'heartbeat' symbol, or the radical symbol, is significant as it represents the operation of finding a square root. It is likened to a heartbeat due to its shape, symbolizing the foundational and vital nature of roots in both mathematics and nature.

  • How does the script explain the concept of principal or positive square roots?

    -The script explains that the square root symbol typically represents the principal or positive result of a square root. This means that when calculating the square root of a number, the symbol refers to the positive solution, unless otherwise specified.

Outlines
00:00
🌱 Understanding Square Roots and Tree Analogies

In the first paragraph, Toby introduces the topic of square roots using the analogy of a tree and its roots. He explains that just as the visible part of a tree is only a small fraction of its total structure, the concept of square roots goes beyond the surface-level understanding of squaring numbers. Toby discusses how square roots are used to find the base of a square, using the example of the square root of 16 being equal to 4. He also touches upon the idea of perfect squares and non-perfect squares, and introduces the concept of negative numbers in the context of square roots, although he notes that for the purposes of this discussion, only positive solutions are considered relevant.

05:06
📐 The Origin and Symbolism of Square Roots

The second paragraph delves into the history and various possible origins of the square root symbol. Toby shares his personal experience of encountering the symbol for the first time and the confusion it caused. He explores different theories about the symbol's etymology, including its possible roots in the Arabic and Latin words for 'root', as well as the idea that it evolved from notations used by mathematicians to mark numbers whose square roots were to be taken. Toby also explains the use of the vinculum in the square root symbol, introduced by Descartes in 1637, and how it signifies the principal or positive result of a square root. He further discusses the concept of imaginary numbers and how they relate to square roots of negative numbers, inviting viewers to explore this topic further in another video.

10:08
🌳 Encouraging Exploration and Mathematical Curiosity

In the final paragraph, Toby encourages viewers to take a walk near trees and ponder the unseen roots, drawing a parallel to the unseen depths of mathematical concepts. He concludes with well wishes for happy studying and the hope that viewers will have a 'mathematical day', emphasizing the joy and beauty that can be found in the study of mathematics.

Mindmap
Keywords
💡Square root
A square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics, especially in the context of this video which uses the analogy of a tree's roots to explain the concept. The square root of 16, for example, is 4, because 4 times 4 equals 16. The video emphasizes the square root as a way to understand the underlying structure or 'roots' of mathematical problems.
💡Logarithms
Logarithms are mathematical functions that can help in rewriting exponents and are used to solve problems involving exponential growth or decay. In the video, logarithms are mentioned as a way to connect with the concept of exponentiation, which is directly related to the theme of squares and square roots discussed later.
💡Exponents
Exponents are a mathematical notation used to denote the number of times a base number is multiplied by itself. For instance, '3 squared' or '3^2' means 3 multiplied by 3, which equals 9. The video uses exponents to introduce the concept of squares and to lead into the discussion of square roots.
💡Perfect squares
Perfect squares are the results of squaring an integer; they are whole numbers that are the product of some integer multiplied by itself. The video mentions numbers like 9, 16, and 25 as examples of perfect squares, which are foundational to understanding the concept of square roots.
💡Negative numbers
In the context of the video, negative numbers are discussed in relation to square roots. While squaring any real number (positive or negative) results in a positive value, the video points out that negative numbers do not have real square roots. However, with the introduction of imaginary numbers, the concept is expanded to include square roots of negative numbers as well.
💡Imaginary numbers
Imaginary numbers are a concept in mathematics that extend the idea of real numbers to include numbers that, when squared, give a negative result. The video introduces the imaginary unit 'i', where i squared equals -1, as a way to handle square roots of negative numbers, such as the square root of -16, which equals 4i.
💡Vinculum
The vinculum is a horizontal line placed over the symbol for a square root that indicates all the numbers under it are included in the square root operation. It is mentioned in the video when discussing the history and notation of square roots, emphasizing its role in grouping the numbers that are under the operation of finding a square root.
💡Radical symbol
The radical symbol, often resembling a heartbeat or a tick, is the mathematical notation used to denote the square root of a number. The video explores the possible origins of this symbol and its standard use in mathematics to represent the operation of finding a square root.
💡Cube root
While the main focus of the video is on square roots, it briefly touches upon other types of roots, such as the cube root. The cube root of a number is a value that, when multiplied by itself three times (raised to the power of three), gives the original number. It is mentioned to illustrate that the concept of roots can be extended beyond just square roots.
💡Fractional powers
Fractional powers extend the concept of exponents to include non-integer values, such as square roots which can be thought of as the second power (or 'two halves'). The video mentions fractional powers in the context of extending the idea of roots to include cube roots and other non-square roots.
💡Area of a square
The area of a square is calculated by multiplying the length of one side by itself. This concept is central to understanding square roots as it relates to the total 'dirt' or area covered by the roots in the video's tree analogy. The area calculation is used to determine the length of a side given the total area, which is key to finding square roots.
Highlights

The importance of a tree's roots is compared to the concept of square roots in mathematics.

Square roots are used to rewrite exponents, such as squares, where a number is multiplied by itself.

The concept of finding the square root of a number, such as the square root of 16 being 4, is introduced.

The analogy of roots providing support to a tree is used to explain the role of square roots in mathematics.

The area of a square is calculated from its base times its height, which is key to understanding square roots.

Perfect squares are numbers that are the squares of whole numbers, such as 9, 16, and 25.

Non-perfect squares, like 20, have square roots that fall between whole numbers, such as 4 and 5.

Negative numbers squared result in positive numbers, so they do not have real square roots, but imaginary numbers can be used.

The symbol for square root, called the radical, is explained with a possible origin from the Arabic or Latin word for root.

The use of the square root symbol with a line over the top, known as the vinculum, was first used by Descartes in 1637.

The principal or positive result of a square root is typically taken, but there can be two solutions for equations like x^2 = 16.

Fractional powers and other roots, such as cube roots, can be expressed using the radical symbol.

Squaring any number, whether positive or negative, results in a positive outcome.

Imaginary numbers are introduced with i^2 = -1, allowing for the square root of negative numbers.

The square root of a negative number, such as -16, is shown to result in an imaginary number, like 4i.

The video encourages viewers to not be limited by traditional thinking and to explore the square roots of imaginary numbers.

A final thought is shared on the beauty of understanding the hidden roots of trees, analogous to the hidden depths of mathematical concepts.

Transcripts

Browse More Related Video

Square Roots, Cube Roots, and Other Roots

Finding the Domain of Functions (Precalculus - College Algebra 4)

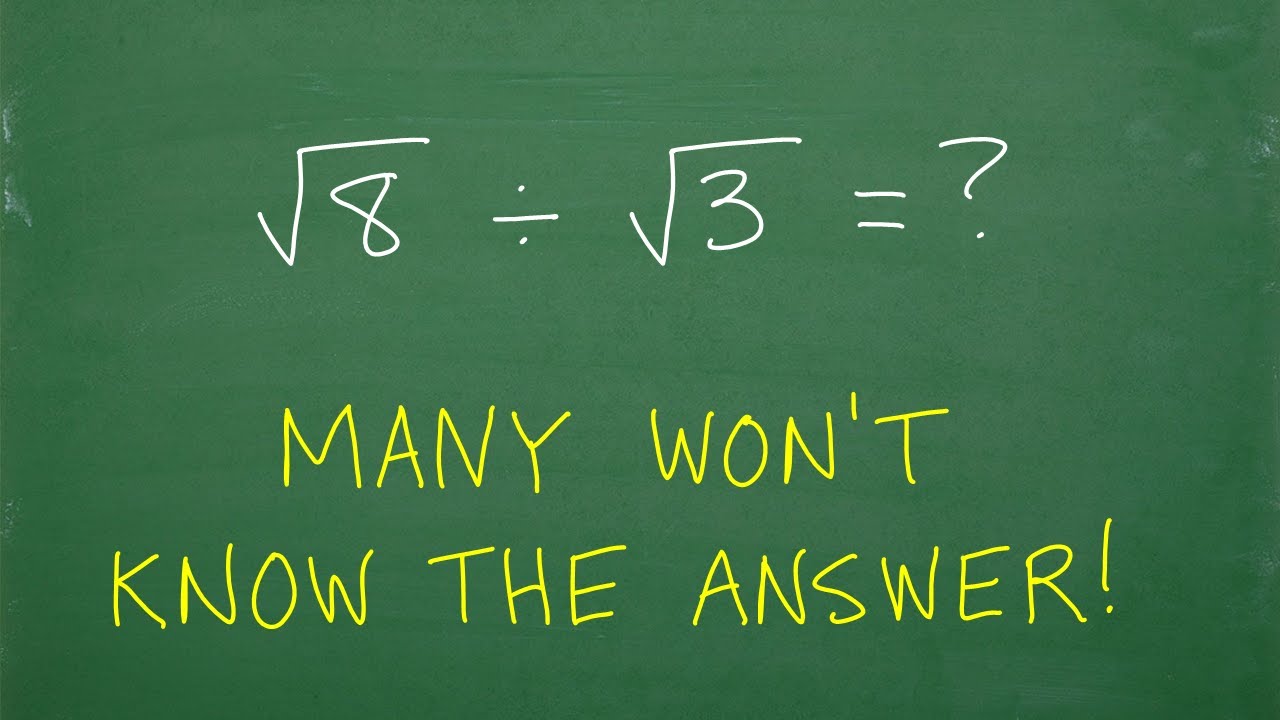
The square root of 8 divided by the square root of 3 =? Many won’t know the ANSWER!

Ch. 1.6 Complex Numbers

Complex Numbers: Operations, Complex Conjugates, and the Linear Factorization Theorem

Add, Subtract, Multiply, Divide Imaginary & Complex Numbers - [1]

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsSquare RootsLogarithmsEducationalTree AnalogyRootsSupportPerfect SquaresImaginary NumbersTobyJoy of MathVisual Learning