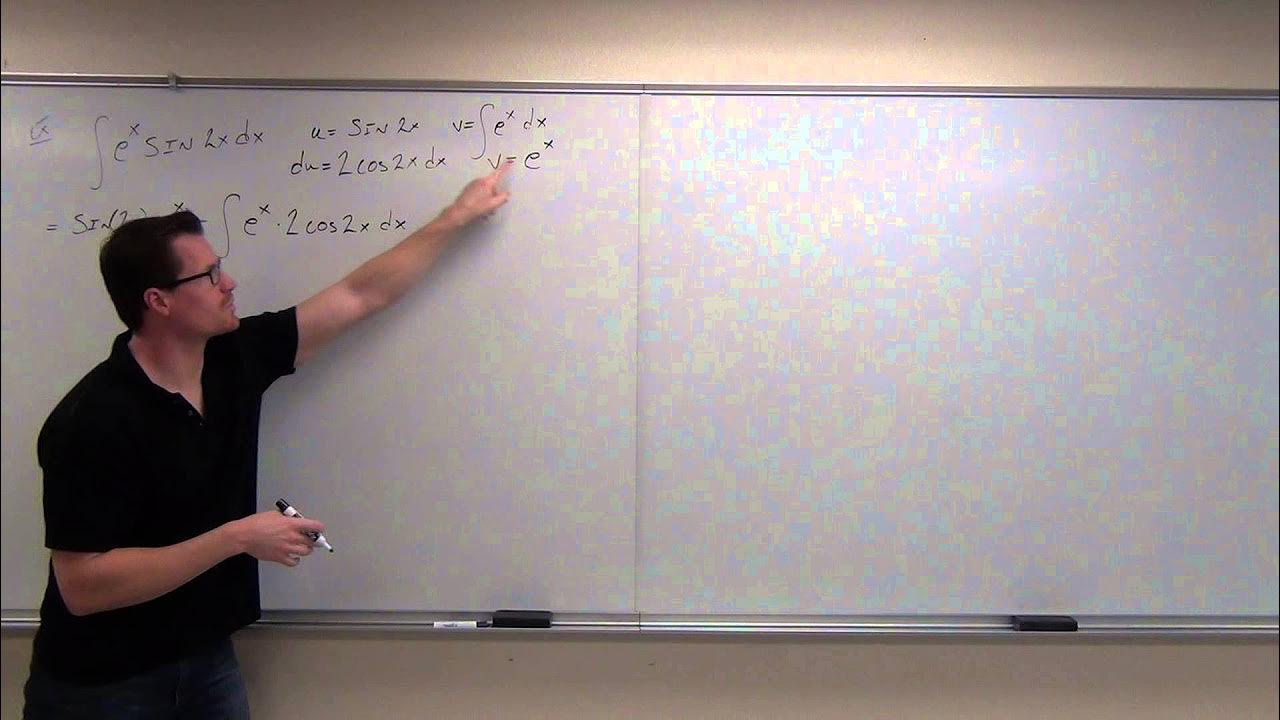BusCalc 13.3 Integration by Parts
TLDRThe video script is an in-depth exploration of advanced calculus techniques, specifically focusing on integration by parts and u-substitution methods. The instructor meticulously guides viewers through the process of integrating complex functions, emphasizing the importance of correctly choosing the u variable for substitution and the application of the anti-derivative power rule. The script delves into the nuances of integration by parts, illustrating how to set up integration tables and correctly pair terms for a precise solution. It also addresses common pitfalls, such as incorrect term selection leading to infinite derivative sequences, and demonstrates how to rectify these errors. The video serves as a comprehensive tutorial for students aiming to master these integral calculus concepts, highlighting the necessity of practice for proficiency in these techniques.
Takeaways
- 📚 When performing integration by substitution, it's crucial to choose the correct variable u to simplify the integral.
- ✍️ During the integration process, it's important to replace variables back to the original form after solving to avoid losing partial credits.
- 🔁 The derivative power rule and the antiderivative power rule are opposites, where the former reduces the exponent by one and the latter increases it by one.
- 🧮 Negative exponents in the denominator can be converted to positive exponents in the numerator, and vice versa, which is key to solving integrals with negative exponents.
- 🔄 Integration by parts is a technique used when the integral does not follow standard rules and cannot be solved by u-substitution; it involves splitting the integrand into two parts.
- 📊 A table can be used to organize the integration by parts process, with alternating signs and columns for derivatives and antiderivatives of the chosen parts.
- 🧵 The 'snake' pattern in integration by parts is a method to pair up terms after filling out the table, which helps in combining the terms to find the final antiderivative.
- 📈 When checking work in integration by parts, taking the derivative of the result should yield the original integrand, confirming the correctness of the process.
- 📌 In integration by parts, it's essential to choose the first part (u) wisely, ensuring that its derivatives eventually lead to zero, which simplifies the process.
- 🤔 The process might seem counterintuitive or complex at first, but with practice, it becomes a valuable tool for solving more complex integrals.
- 📝 Memorizing the antiderivative of common functions, such as natural logarithms and exponentials, is beneficial for efficiently solving integration by parts problems.
Q & A
What is the process of integration by parts?
-Integration by parts is a method used to find the antiderivative of a product of two functions that cannot be easily integrated using standard methods. The process involves splitting the integrand into two parts, taking derivatives and antiderivatives of these parts, and then combining them using a specific formula to find the final antiderivative.
How do you choose the 'u' and 'dv' for integration by parts?
-When using integration by parts, you choose one part of the integrand to be 'u' and the other part to be 'dv'. A common guideline is to take the function that becomes simpler after differentiation as 'u', and the function that is easier to integrate as 'dv'. For example, with exponential functions, the exponential part is usually chosen as 'dv', and with logarithmic functions, the logarithm is chosen as 'u'.
What is the formula for integration by parts?
-The formula for integration by parts is derived from the product rule for differentiation and is given by: ∫(u dv) = u*v - ∫(v du). Here, 'u' and 'v' are the chosen parts of the integrand, 'du' and 'dv' are their respective derivatives, and the process involves finding the antiderivative of 'v' and differentiating 'u'.
Why is it important to check your work after finding an antiderivative?
-Checking your work by differentiating the found antiderivative is important to ensure that you have correctly applied the integration method and arrived at the correct result. If the derivative of the antiderivative does not match the original integrand, it indicates a mistake in the integration process.
What is the antiderivative of e^u in terms of u?
-The antiderivative of e^u with respect to u is simply e^u, plus a constant of integration (C).
How does the choice of u and dv affect the complexity of the integration by parts process?
-The choice of u and dv directly affects the complexity of the integration by parts process. If the derivative of u does not eventually become zero or simpler with each iteration, the process can become cumbersome and infinite. Therefore, it is crucial to choose u and dv wisely to ensure that the process terminates and yields a solvable problem.
What is the role of the constant C in antiderivative problems?
-The constant C is used to represent an arbitrary constant of integration. It is added to the final answer of an antiderivative problem because the derivative of a constant is zero, which means that when finding an antiderivative, we are essentially 'undoing' the derivative process, which can result in an infinite number of original functions that all have the same derivative. The constant C accounts for this ambiguity.
Why is it said that the antiderivative power rule is the opposite of the derivative power rule?
-The antiderivative power rule is considered the opposite of the derivative power rule because while the derivative power rule involves reducing the exponent by one (d/dx[x^n] = n*x^(n-1)), the antiderivative power rule involves increasing the exponent by one when finding the antiderivative of x^n (∫x^n dx = x^(n+1)/(n+1) + C), and then dividing by the new exponent.
What is the purpose of the table with alternating plus and minus signs used in integration by parts?
-The table with alternating plus and minus signs is a systematic way to apply the integration by parts formula. It helps to organize the derivatives of 'u' and the antiderivatives of 'dv' in a clear pattern, which aids in correctly pairing and combining terms to find the final antiderivative.
How does the process of integration by parts relate to the product rule for derivatives?
-Integration by parts is essentially the reverse process of the product rule for derivatives. The product rule states that the derivative of a product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first. Integration by parts uses this relationship to break down the process of finding antiderivatives of products of functions that do not follow standard rules.
What is the significance of the horizontal snake in the integration by parts table?
-The horizontal snake in the integration by parts table signifies the termination of the process with an antiderivatives term. When a horizontal line is used, it means that the next step involves taking the antiderivative of the term that resulted from the horizontal pairing. This is particularly useful when dealing with logarithmic functions in the integrand.
Outlines
📚 U-Substitution Integration Technique
The paragraph introduces the U-substitution method for integration, demonstrating the process of substituting 'u' for a part of the integral, differentiating 'u' with respect to 'x', and then simplifying the integral. It emphasizes the importance of returning the answer to the original variable, in this case, 'x', and the common mistake of not doing so.
🧮 Integration by Parts: Choosing U and Solving for DT
This section explains the second part of the integration by parts process, focusing on selecting an appropriate 'u' and calculating 'dt'. It details the steps to rearrange the integral to solve for 'dt' and apply the integration by parts formula, highlighting the importance of factoring out common terms and the power rule for antiderivatives.
🔍 Checking Work with Derivatives
The paragraph discusses the importance of verifying the correctness of an integral solution by differentiating the antiderivative and comparing it to the original integrand. It also touches on the concept of negative exponents and the relationship between the derivative and antiderivative power rules.
📝 Integration by Parts Procedure
This part outlines the procedure for integration by parts, explaining how to split the integrand into two parts and create a table to take derivatives and antiderivatives. It emphasizes the method's iterative nature and the process of pairing terms to find the final antiderivative.
🎓 Example Application of Integration by Parts
The paragraph provides a worked example of integration by parts, illustrating the process with the integral of x squared times e to the x. It shows how to fill out the integration by parts table, pair terms, and combine them to obtain the final answer, including the constant of integration.
🤔 Verifying Antiderivatives with the Product Rule
This section discusses how to check the correctness of an antiderivative by applying the product rule to the antiderivative and comparing it to the original integrand. It also addresses the cancellation of terms in the derivative and the importance of the product rule in these checks.
📉 Integration by Parts with Natural Logarithms
The paragraph explores the use of integration by parts with natural logarithms, explaining the process of setting up the integration by parts table and the peculiarities of horizontal 'snakes' in the table. It also demonstrates how to handle the antiderivative of one in the context of logarithmic integrals.
🔁 The Flexibility of Integration by Parts
This section highlights the flexibility of the integration by parts method, showing that regardless of how many rows are included in the table or how many 'snakes' are used, the final answer remains consistent. It emphasizes the importance of terminating with a horizontal 'snake' and the mathematical reasoning behind the method.
📌 Correct Choice in Integration by Parts
The paragraph discusses the importance of making the correct choice of 'u' and 'dv' in the integration by parts formula. It provides an example where an incorrect choice leads to an infinite series, illustrating how to recognize and correct the mistake by flipping the chosen parts and restarting the process.
🧵 Derivation of the Integration by Parts Formula
This section delves into the mathematical derivation of the integration by parts formula, starting from the product rule for derivatives. It explains how to rearrange and take antiderivatives of both sides of the product rule to arrive at the integration by parts formula, justifying the method's validity.
📐 Alternative Presentation of Integration by Parts
The paragraph presents an alternative way the integration by parts formula may be encountered, particularly in online resources, where 'u' and 'dv' are used to represent the parts of the integral. It reassures students that understanding and applying the formula is more important than memorizing different notations.
📝 Final Integration by Parts Example
The final part provides another example of using integration by parts, this time with a natural logarithm function. It walks through the process of setting up the integration by parts table, pairing terms, and calculating the antiderivative, including the steps to handle the horizontal section and the importance of including the constant of integration.
🤓 The Derivative Chain Rule and Antiderivatives
This section discusses the peculiarity of the derivative of natural logarithm functions and how the chain rule affects the derivative of natural logarithms multiplied by a constant. It explains the apparent loss of information in the derivative and how the constant can be reintroduced through the constant of integration 'c', resolving the seeming contradiction.
📝 Practice Makes Perfect
The concluding paragraph emphasizes the necessity of practice for mastering techniques such as U-substitution, antiderivatives, and integration by parts. It advises students to diligently practice these methods to succeed in their exams, highlighting that proficiency will not come naturally without effort.
Mindmap
Keywords
💡Integration by Parts
💡u-substitution
💡Antiderivative
💡Chain Rule
💡Derivative
💡Exponential Function
💡Product Rule
💡Natural Logarithm
💡Power Rule
💡Reciprocal Rule
Highlights
The process of integration by substitution is explained, emphasizing the need to replace a complex integrand with a simpler one, denoted as 'u'.
The importance of correctly choosing the substitution variable 'u' is highlighted, as it can simplify the integral and make it solvable.
The concept of reverse substitution is discussed, which involves returning the solution back to the original variable after solving the integral in terms of 'u'.
The use of the derivative power rule and the antiderivative power rule are contrasted, showing they are opposite in their mathematical operations.
The method of checking work by differentiating the antiderivative to see if it matches the original integrand is introduced as a validation technique.
Integration by parts is introduced as a technique for finding antiderivatives of products of functions that do not follow standard rules.
A step-by-step example of integration by parts is provided, illustrating the process with a specific integral.
The significance of the product rule in derivatives is tied to the integration by parts formula, providing a theoretical foundation for the technique.
The concept of 'u' and 'dv' is introduced as a shorthand for the parts of the integrand chosen for integration by parts.
The choice of which part of the integrand to treat as 'u' or 'dv' is emphasized as crucial for successfully applying integration by parts.
An incorrect choice in the application of integration by parts is demonstrated, showing how it can lead to an unsolvable integral.
The correct application of integration by parts for the same integral is shown, resulting in a solvable form.
The technique of horizontal integration by parts is introduced, which involves taking the antiderivative of a term in the integration by parts process.
The importance of practice in mastering u-substitution and integration by parts is stressed for success in exams.
The peculiar behavior of the derivative of natural log functions with respect to 't' is explored, noting it is always 1/t regardless of the multiplier.
An explanation is provided for why taking the antiderivative of the derivative of natural log functions results in a loss of the multiplier, which is resolved by the flexibility of the constant 'c'.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: