Business Calculus - Math 1329 - Section 2.2 - Techniques of Differentiation
TLDRThe video script provides a comprehensive overview of derivative calculus, focusing on the shortcut rules for finding derivatives. It begins with the power rule, illustrating how to find the derivative of a function in the form of x^n by bringing down the power and multiplying by x raised to the power of n-1. The script then covers the constant multiple property, explaining that the derivative of a constant times a function is the constant times the derivative of the function. Sum and difference properties are also discussed, showing that the derivative of a sum or difference of functions is the sum or difference of their derivatives. The script includes examples of finding derivatives using these rules and touches on the derivative of a number being zero. It concludes with an application of derivatives in a medical context, calculating the rate of virus spread using a given function and its derivative, emphasizing the importance of derivatives in understanding rates of change.
Takeaways
- 📚 The derivative represents the slope of the tangent line to a curve at a particular point, indicating the instantaneous rate of change.
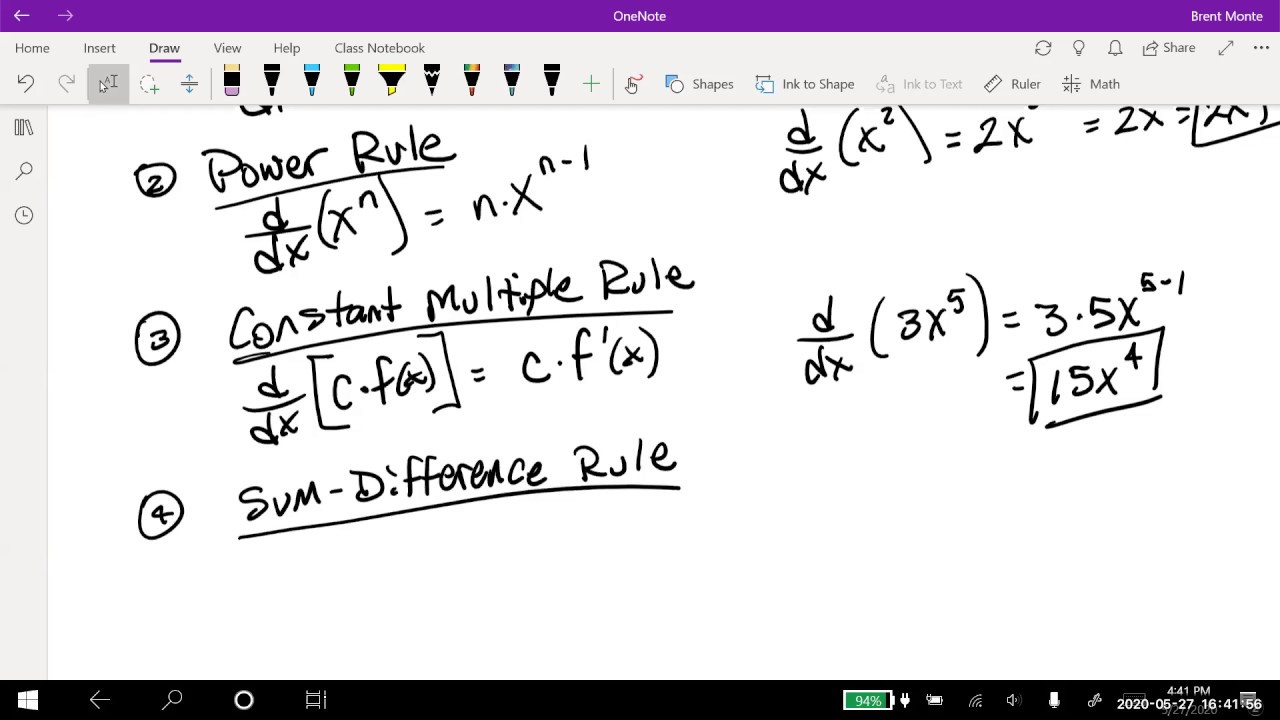
- 🔑 The power rule states that the derivative of f(x) = x^n is f'(x) = n · x^{n-1}, which simplifies the process of finding derivatives.
- 📌 Example: For f(x) = x^6, the derivative f'(x) is 6x^5, following the power rule by bringing down the exponent and adjusting the power.
- ➗ When dealing with functions like f(x) = 1/x^4, rewrite as x^{-4} before applying the power rule, resulting in f'(x) = -4/x^5.
- 🚫 Remember not to use equal signs between the original function and its derivative; they are separate functions.
- 📉 The constant multiple property allows you to find the derivative of a constant times a function by multiplying the constant by the derivative of the function.
- 🔠 For sums and differences of functions, the derivative is the sum or difference of the derivatives of the individual functions.
- 🔢 The derivative of a constant is zero, which is a straightforward rule that simplifies finding derivatives of terms without the variable.
- ➖ To find where a function has a horizontal tangent, set the derivative equal to zero and solve for the variable, as the slope of the tangent line must be zero.
- 🧬 In a medical context, the derivative can represent the rate at which a virus spreads, calculated by finding the derivative of the infection function and evaluating it at a specific time.
- 🎓 Memorizing the derivative of common functions, such as √x or x^n, is beneficial for quickly solving problems without going through the derivation process each time.
Q & A
What does the term 'derivative' represent in the context of calculus?
-In calculus, the term 'derivative' represents the slope of the tangent line to a curve at a given point, which also signifies the instantaneous rate of change of a function at that point.
What is the power rule for derivatives?
-The power rule states that for a function f(x) = x^n, the derivative f'(x) is equal to n * x^(n-1). It means you bring the power down to the front and multiply by x raised to one less than the original power.
How do you find the derivative of a function with a negative exponent?
-To find the derivative of a function with a negative exponent, you first rewrite the function with the base x in the numerator (e.g., x^(-n) becomes 1/x^n), then apply the power rule, and finally return the answer to the original form if necessary.
What is the constant multiple property in the context of derivatives?
-The constant multiple property states that if f(x) = k * g(x), where k is a constant, then the derivative f'(x) = k * g'(x). This means you keep the constant as a multiplier and multiply it by the derivative of the other function.
How does the sum and difference properties for derivatives work?
-The sum and difference properties state that for a function f(x) = g(x) + h(x), the derivative f'(x) = g'(x) + h'(x), and for f(x) = g(x) - h(x), the derivative f'(x) = g'(x) - h'(x). This allows you to find the derivative of a sum or difference of functions by finding the derivatives of the individual functions and adding or subtracting them.
What does it mean for a function to have a horizontal tangent line?
-A function has a horizontal tangent line at a point where the slope of the tangent line is zero. This occurs where the derivative of the function, f'(x), is equal to zero.
How do you find the rate at which a quantity is changing in relation to another quantity?
-To find the rate at which a quantity is changing in relation to another, you take the derivative of the function representing the quantity with respect to the other quantity. The derivative represents the rate of change or the slope of the tangent line at a particular point.
What is the derivative of the square root function, and how is it represented?
-The derivative of the square root function, f(x) = √x or x^(1/2), is f'(x) = 1/(2√x) or (1/2)x^(-1/2). This derivative is often memorized as it frequently appears in calculus problems.
How do you find the number of people infected after a certain number of days using a given function?
-You substitute the given number of days (T) into the function that represents the number of people infected (n(T)). Then, you perform the calculation to find the number of people infected at that specific time.
What does the notation dy/dx represent?
-The notation dy/dx represents the derivative of y with respect to x. It is another way to express the slope of the tangent line to the curve of the function y = f(x) at a particular point, which is the rate of change of y per unit change in x.
How do you determine the points where a function has a horizontal tangent?
-To determine the points where a function has a horizontal tangent, you first find the derivative of the function. Then, you set the derivative equal to zero and solve for the variable (usually x). The solutions will give you the x-values where the tangent is horizontal.
Outlines
📚 Introduction to Derivatives and Power Rule
This paragraph introduces the concept of derivatives and focuses on shortcut rules for finding them. The power rule is explained, which states that the derivative of X to the power of N is N times X to the power of N minus 1. Examples are provided to illustrate the process of taking derivatives using the power rule, including functions with positive and negative exponents. The importance of not equating the original function with its derivative is emphasized, and the process of rewriting functions to apply the power rule is demonstrated.
🔢 Constant Multiple Property and Sum/Difference Properties
The second paragraph delves into the constant multiple property, which allows for the differentiation of a constant multiplied by a function. It explains that the derivative of such a function is the constant multiplied by the derivative of the function. The sum and difference properties for derivatives are also introduced, showing how to find the derivative of a sum or difference of functions by adding or subtracting their respective derivatives. Examples are given to illustrate these concepts, including functions with multiple terms and those involving constants and powers of X.
🔍 Derivatives of Functions with Fractions and Roots
This paragraph addresses the process of finding derivatives for functions that include fractions and roots. It demonstrates how to rewrite functions with fractions to have their variables in the numerator and how to apply the power rule to roots expressed as fractional exponents. The concept of dy/dx as a notation for derivatives is introduced, and an example is given to show how to find the derivative of a function involving a fifth root and a negative exponent. The process of simplifying derivatives and reverting them to their original function's form is also discussed.
🔑 Horizontal Tangent Lines and Factoring
The fourth paragraph discusses how to find points where a function has a horizontal tangent line, which corresponds to where the derivative is equal to zero. It guides through finding the derivative of a given function and setting it to zero to solve for the variable. Factoring is used to find the values of the variable that result in a horizontal tangent. The process is illustrated with an example function, leading to the discovery of specific points where the tangent is horizontal.
📈 Application of Derivatives in a Real-World Scenario
The final paragraph presents a real-world application of derivatives, specifically in the context of a medical team researching the spread of a virus. It shows how to use a given function to determine the number of people infected after a certain number of days. The derivative of the function is then found to calculate the rate at which the virus is spreading. The example concludes with evaluating the derivative at a specific time to find the rate of infection and emphasizes the difference between counting whole numbers of people and calculating rates of change, which can be fractional.
Mindmap
Keywords
💡Derivative
💡Power Rule
💡Instantaneous Rate of Change
💡Constant Multiple Property
💡Sum and Difference Properties
💡Tangent Line
💡Slope of a Line
💡Square Root Function
💡Exponential Function
💡Rate of Change
💡Horizontal Tangent
Highlights
The concept of the derivative is introduced as the slope of the tangent line and the instantaneous rate of change.
Shortcut rules for finding derivatives are presented to simplify the process.
The power rule for derivatives is explained, where the derivative of X to the N power is N times X to the N minus 1.
Examples are provided to illustrate the application of the power rule to various functions.
The constant multiple property is introduced, stating that the derivative of a constant times a function is the constant times the derivative of the function.
Sum and difference properties for derivatives are discussed, allowing for the derivative of a sum or difference of functions to be found by adding or subtracting their derivatives.
The derivative of a function involving a sum of terms is demonstrated step by step.
The importance of treating the function and its derivative as separate entities when applying the rules is emphasized.
The derivative of a function with a fractional part is shown, including the process of rewriting the function to facilitate differentiation.
The dy/dx notation is introduced as an alternative to the function notation for derivatives, highlighting its utility in various mathematical contexts.
A method for finding where a function has a horizontal tangent line is demonstrated by setting the derivative equal to zero and solving for the variable.
An example of a real-world application of derivatives is given, where the spread of a virus is modeled mathematically, and the rate of infection is found using the derivative.
The derivative of the square root function is derived and simplified into a memorizable form.
The concept of rate of change is connected to the derivative, and its decimal representation is justified in the context of the problem.
The distinction between using whole numbers for discrete quantities (like people) and decimals for rates of change (like people per day) is clarified.
The process of differentiating a function with a radical is detailed, emphasizing the importance of correctly applying the power rule and reverting to the original function's form.
The transcript concludes with a reminder of the importance of understanding and applying the derivative rules correctly, especially when dealing with real-world problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: