CHEM 201: Calculating Equilibrium Concentrations from K and Initial Values – Quadratic Formula
TLDRThe video script details a chemistry problem involving the calculation of equilibrium concentrations using the equilibrium constant and initial concentrations. It begins with setting up a RICE table for the reaction involving bromine, chlorine, and BrCl gas. The reaction quotient is calculated to determine the direction needed to reach equilibrium. Since the reaction quotient is less than the equilibrium constant, the reaction will shift to produce more BrCl. Using the quadratic formula, the problem is solved for x, which represents the change in concentration. The valid solution for x is identified by ensuring all concentrations remain positive. The equilibrium concentration of BrCl is found to be 0.60 molar, confirmed by substituting back into the equilibrium constant expression. The video provides a step-by-step guide on solving chemical equilibrium problems using the quadratic formula, emphasizing the importance of positive concentrations and the correct application of chemical principles.
Takeaways
- 🧪 To find the equilibrium concentrations, a RICE table is used, starting with the reaction and initial concentrations.
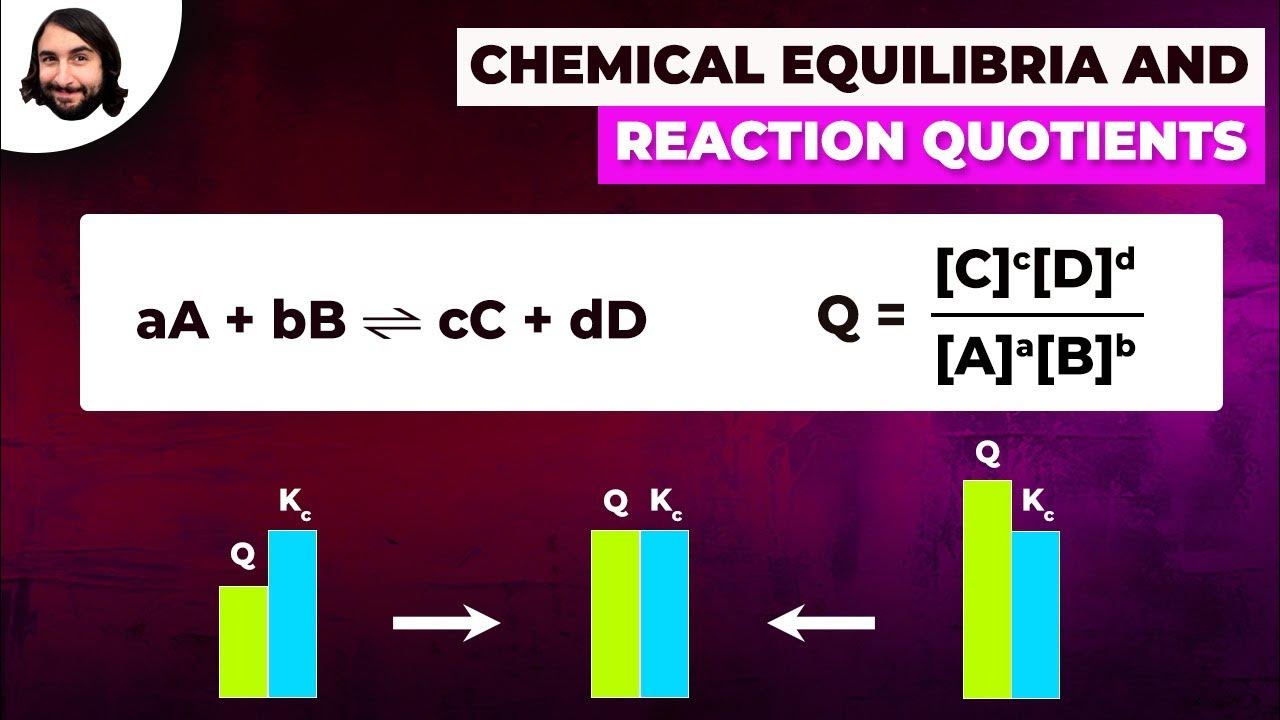
- 🔍 The change in concentration is determined by calculating the reaction quotient (Q) using the current concentrations.
- ⚖️ If the reaction quotient Q is less than the equilibrium constant (KC), the reaction will shift to produce more product.
- 📉 The change in concentrations is represented as -x, -x, and +2x, derived from the balanced chemical equation coefficients.
- 🧮 The equilibrium concentrations are calculated by adding the initial concentrations to the changes (initial + change = equilibrium).
- 🔢 The quadratic formula is employed to solve for x when the equation cannot be factored into perfect squares.
- 📝 The equation is set up in the form 0 = Ax^2 + Bx + C by multiplying both sides by the denominator (0.30-x)(0.40-x).
- 🔑 The FOIL method is used to expand the equation and combine like terms to get the quadratic equation.
- 🔁 The quadratic formula is applied with A, B, and C values derived from the equation to find the possible values for x.
- ✅ Only the value of x that results in all positive concentrations when substituted back into the equilibrium row is valid.
- 📊 The final concentration of BrCl at equilibrium is determined by substituting the valid value of x into the equilibrium row.
- 🔄 To verify the solution, the value of x is substituted back into the equilibrium constant expression to match the given KC value.
Q & A
What is the purpose of creating a RICE table in the context of the given script?
-A RICE table is used to organize the initial concentrations, changes in concentrations, and equilibrium concentrations for a chemical reaction. It helps to visualize and solve for the unknown concentrations at equilibrium.
What is the reaction quotient (Q) and how is it used in the script?
-The reaction quotient (Q) is a value calculated using the current concentrations of reactants and products in a chemical reaction. It is used to determine the direction in which the reaction will proceed to reach equilibrium. If Q is less than the equilibrium constant (KC), the reaction will shift to produce more products.
Why is it necessary to calculate the change in concentration (represented as -x, -x, and +2x) in the script?
-The change in concentration is necessary to determine the shift towards equilibrium. The values -x, -x, and +2x represent the decrease in concentrations of bromine and chlorine gases, and the increase in BrCl gas, respectively, based on the stoichiometry of the balanced chemical equation.
How is the equilibrium constant (KC) used in the quadratic formula to solve for x?
-The equilibrium constant (KC) is used to set up an equation with the equilibrium concentrations. By substituting the equilibrium concentrations into the KC expression and rearranging it into the standard quadratic form (0 = Ax^2 + Bx + C), the quadratic formula can be applied to solve for x, which represents the change in concentration at equilibrium.
What is the FOIL method and how is it applied in the script?
-The FOIL method is a technique for multiplying two binomials. It stands for First, Outer, Inner, Last, and is used to expand the product of two binomials. In the script, it is used to expand the expression (0.30 - x)(0.40 - x) to help set up the quadratic equation.
Why are both solutions from the quadratic formula (0.10 and 2.8) not valid?
-Not all solutions from the quadratic formula are valid because they must result in physically meaningful concentrations. If substituting a solution back into the equilibrium row of the RICE table results in a negative concentration, it is not a valid solution. Only the solution that yields all positive concentrations is considered valid.
How is the correct value of x determined in the script?
-The correct value of x is determined by substituting both solutions from the quadratic formula back into the equilibrium row of the RICE table. The solution that results in all positive concentrations is considered correct. In the script, x = 0.10 leads to concentrations of 0.20, 0.30, and 0.60 molar, which are all positive and thus valid.
What is the final concentration of BrCl at equilibrium according to the script?
-The final concentration of BrCl at equilibrium is 0.60 molar, as determined by substituting the correct value of x (0.10) back into the equilibrium row of the RICE table.
How is the validity of the solution for x confirmed in the script?
-The validity of the solution for x is confirmed by substituting the value of x back into the equilibrium constant expression. If the calculated value matches the given KC, it confirms that x was solved correctly using the quadratic equation.
What is the significance of the equilibrium constant (KC) in the context of the script?
-The equilibrium constant (KC) is a measure of the extent to which a reaction proceeds to completion. In the script, it is used to determine the direction in which the reaction will shift to reach equilibrium and to validate the solution for x by ensuring that the calculated value matches the given KC.
Why is it important to double-check the solution for x by substituting it back into the equilibrium constant expression?
-Double-checking the solution for x is important to ensure the accuracy of the calculations and to confirm that the derived equilibrium concentrations are consistent with the given equilibrium constant. This step helps validate the entire problem-solving process.
What does the term 'quadratic formula' refer to in the context of the script?
-In the context of the script, the quadratic formula is a mathematical formula used to find the solutions for x in a quadratic equation of the form 0 = Ax^2 + Bx + C. It is essential for solving for the change in concentration (x) when the reaction quotient and equilibrium constant are known.
Outlines
🧪 Calculating Equilibrium Concentrations with Quadratic Formula
This paragraph explains the process of calculating the concentration of BrCl at equilibrium using the equilibrium constant and initial concentrations. The example involves a reaction vessel with initial amounts of bromine, chlorine, and BrCl gases. A RICE table is constructed to outline the reaction and initial concentrations. The reaction quotient is calculated to determine the direction needed to reach equilibrium. Since the reaction quotient is less than the equilibrium constant, the reaction will shift to the right, leading to a change in concentrations. The equilibrium concentrations are found by solving for x using the quadratic formula after setting up the equilibrium constant expression with the equilibrium row values. The quadratic formula is applied to find x, and only the solution that results in positive concentrations is valid. The concentration of BrCl at equilibrium is determined to be 0.60 molar after substituting the valid x value back into the equilibrium row. The solution is verified by ensuring that the equilibrium constant expression holds true with the calculated x value.
📐 Verification of the Quadratic Solution with KC Value
The second paragraph focuses on the verification process of the solution obtained from the quadratic equation. By substituting the calculated value of x (0.10) back into the equilibrium constant expression, the result should match the given KC value (6.0) if the solution is correct. This step confirms that the quadratic equation was solved accurately and that the equilibrium concentrations are valid. The verification step is crucial to ensure the correctness of the equilibrium concentrations and to validate the mathematical approach taken in the problem-solving process.
Mindmap
Keywords
💡Equilibrium concentrations
💡Equilibrium constant (KC)
💡RICE table
💡Reaction quotient (Q)
💡Quadratic formula
💡FOIL method
💡Negative concentration
💡Bromine gas
💡Chlorine gas
💡BrCl gas
💡Valid solution
Highlights
Calculating equilibrium concentrations using the equilibrium constant and initial concentrations.
Solving for x with the quadratic formula in a chemical equilibrium problem.
Initial concentrations of bromine, chlorine, and BrCl gases provided for the reaction vessel.
Constructing a RICE table to organize the reaction and initial concentrations.
Determining the direction of the reaction shift to reach equilibrium using the reaction quotient.
Substituting current concentrations into the equilibrium constant expression to calculate Q.
Reaction quotient Q is found to be 1.3, indicating a shift to produce more product.
Deducing the change in concentrations as -x, -x, and +2x based on the balanced chemical equation.
Establishing the equilibrium concentrations by adding the initial and change rows.
Using the equilibrium constant expression to solve for x with the equilibrium concentrations.
Multiplying both sides of the equation by the denominator to prepare for the quadratic formula.
Applying the FOIL method to expand the equation terms.
Combining like terms to simplify the equation to 2x squared -5.8x + 0.56 = 0.
Using the quadratic formula to find the values of x.
Identifying valid x values that result in positive concentrations for all reactants and products.
Plugging in x = 0.10 to find the equilibrium concentrations: 0.20 M bromine, 0.30 M chlorine, and 0.60 M BrCl.
Rejecting x = 2.8 as it leads to negative concentrations, which are not valid in chemical equilibrium.
Verifying the correct value of x by substituting it back into the equilibrium constant expression to match the given KC value.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: